山西省吕梁市交城县2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-06-25 类型:期中考试
一、单选题
-
1. “5的算术平方根”这句话用数学符号表示为( )A、 B、 C、 D、2. 某电影院里排号可以用数对表示,小明买了排号的电影票,用数对可表示为( )A、 B、 C、 D、3. 在下列四个实数中,最小的实数是( )A、 B、 C、0 D、4. 如图,下列条件中,不能判定的是( )
 A、 B、 C、 D、5. 如图,点是平面直角坐标系中的一点,轴,轴,则的长为( )
A、 B、 C、 D、5. 如图,点是平面直角坐标系中的一点,轴,轴,则的长为( ) A、 B、3 C、 D、46. 如图,以单位长度为边长作正方形,以原点为圆心,正方形的对角线长为半径画弧,与正半轴的交点就表示 , 与负半轴的交点就表示 . 这种说明问题的方式体现的数学思想方法叫做( )
A、 B、3 C、 D、46. 如图,以单位长度为边长作正方形,以原点为圆心,正方形的对角线长为半径画弧,与正半轴的交点就表示 , 与负半轴的交点就表示 . 这种说明问题的方式体现的数学思想方法叫做( )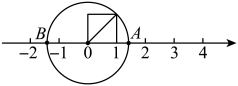 A、分类讨论 B、数形结合 C、代入法 D、换元法7. 下列说法正确的是( )A、两个角的和等于平角时,这两个角互为补角 B、内错角相等 C、两条直线被第三条直线所截,同位角相等 D、过直线外一点作已知直线的垂线段,这条垂线段就是这点到已知直线的距离8. 如图,已知 , , , 则的度数为( )
A、分类讨论 B、数形结合 C、代入法 D、换元法7. 下列说法正确的是( )A、两个角的和等于平角时,这两个角互为补角 B、内错角相等 C、两条直线被第三条直线所截,同位角相等 D、过直线外一点作已知直线的垂线段,这条垂线段就是这点到已知直线的距离8. 如图,已知 , , , 则的度数为( ) A、 B、 C、 D、9. 下列各组数大小比较正确的是( )A、 B、 C、 D、10. 把点A先向左平移2个单位长度,再向上平移3个单位长度得到点B,点B正好落在轴上,则点B的坐标为( )A、 B、 C、 D、
A、 B、 C、 D、9. 下列各组数大小比较正确的是( )A、 B、 C、 D、10. 把点A先向左平移2个单位长度,再向上平移3个单位长度得到点B,点B正好落在轴上,则点B的坐标为( )A、 B、 C、 D、二、填空题
-
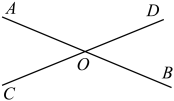
11. 如图,直线相交于点 , 若 , 则的度数为 .
 12. 将交城卦山风景区中的半道亭,白塔,书院分别记为点A,B,C,若建立平面直角坐标系,将A,B用坐标表示为和 , 则书院C用坐标表示为 .
12. 将交城卦山风景区中的半道亭,白塔,书院分别记为点A,B,C,若建立平面直角坐标系,将A,B用坐标表示为和 , 则书院C用坐标表示为 . 13. 如图,将沿方向平移至处,连接 . 若 , 则的长为 .
13. 如图,将沿方向平移至处,连接 . 若 , 则的长为 .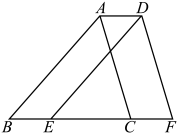 14. 观察下列等式:
14. 观察下列等式:第1个等式: ,
第2个等式: ,
第3个等式: ,
第4个等式: ,
…
按上述规律,请写出第n个等式: .
15. 如图,已知 , 若 , 则的度数为 .
三、解答题
-
16.(1)、计算:(2)、解方程:17. 一个数的算术平方根为2M-6,平方根为±(M-2),求这个数.
18. 在平面直角坐标系中,已知点M .(1)、若点M在轴上,求的值;(2)、若点 , 且直线轴,求线段的长.19. 已知直线与相交于点O,于点O, , 若 , 求的度数. 20. 如图,在平面直角坐标系中,三角形的顶点都在网格格点上,其中B点坐标为 .
20. 如图,在平面直角坐标系中,三角形的顶点都在网格格点上,其中B点坐标为 . (1)、请写出点A,点C的坐标;(2)、将先向左平移3个单位长度,再向上平移4个单位长度,得到 . 请画出平移后的三角形,并写出的三个顶点的坐标;(3)、求的面积.21. 如图,在中,点D在上, , , 垂足分别为E,F.
(1)、请写出点A,点C的坐标;(2)、将先向左平移3个单位长度,再向上平移4个单位长度,得到 . 请画出平移后的三角形,并写出的三个顶点的坐标;(3)、求的面积.21. 如图,在中,点D在上, , , 垂足分别为E,F.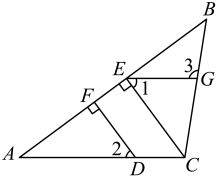 (1)、请判定与平行吗?并说明理由;(2)、如果 , 且 , 求的度数.22. 如图1,在平面直角坐标系中,点A,B的坐标分别是(-2,0),(4,0),现同时将点A、B分别向上平移2个单位长度,再向右平移2个单位长度,得到A,B的对应点C,D.连接AC、BD、CD.
(1)、请判定与平行吗?并说明理由;(2)、如果 , 且 , 求的度数.22. 如图1,在平面直角坐标系中,点A,B的坐标分别是(-2,0),(4,0),现同时将点A、B分别向上平移2个单位长度,再向右平移2个单位长度,得到A,B的对应点C,D.连接AC、BD、CD. (1)、点C的坐标为 , 点D的坐标为 , 四边形ABDC的面积为 .(2)、在x轴上是否存在一点E,使得△DEC的面积是△DEB面积的2倍?若存在,请求出点E的坐标;若不存在,请说明理由.23. 将一副三角板按如图所示的方式叠放在一起,当且点E在直线的上方时,解决下列问题(提示:).
(1)、点C的坐标为 , 点D的坐标为 , 四边形ABDC的面积为 .(2)、在x轴上是否存在一点E,使得△DEC的面积是△DEB面积的2倍?若存在,请求出点E的坐标;若不存在,请说明理由.23. 将一副三角板按如图所示的方式叠放在一起,当且点E在直线的上方时,解决下列问题(提示:). (1)、①若 , 则的度数为;②若 , 则的度数为;(2)、请猜想与的数量关系,并说明理由;(3)、随着的度数的变化,边是否能与三角板的一边平行?若存在,请直接写出的度数的所有值;若不存在,请说明理由.
(1)、①若 , 则的度数为;②若 , 则的度数为;(2)、请猜想与的数量关系,并说明理由;(3)、随着的度数的变化,边是否能与三角板的一边平行?若存在,请直接写出的度数的所有值;若不存在,请说明理由.