山西省晋中市寿阳县2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-06-25 类型:期中考试
一、单选题
-
1. 计算20( )A、0 B、1 C、2 D、﹣22. 斑叶兰的种子小得简直像灰尘一样,1亿粒斑叶兰种子才50克重,因种子太小,只有放在显微镜下才能看清它的真面目,它的一粒种子重约0.0000005克,数据0.0000005用科学记数法表示为( )A、 B、 C、 D、3. 如图,与是内错角的是( )
 A、∠2 B、∠3 C、∠4 D、∠54. 太阳能作为一种新型能源,被广泛应用到实际生活中,在利用太阳能热水器来加热的过程中,热水器里水的温度随着太阳光照射时间的变化而变化,这一变化过程中因变量是( )A、热水器里水的温度 B、太阳光的强弱 C、太阳光照射的时间 D、热水器的容积5. 下列算式能用平方差公式计算的是( )A、 B、 C、 D、6. 如图,将一副三角尺按不同位置摆放,摆放方式中的图形有( )
A、∠2 B、∠3 C、∠4 D、∠54. 太阳能作为一种新型能源,被广泛应用到实际生活中,在利用太阳能热水器来加热的过程中,热水器里水的温度随着太阳光照射时间的变化而变化,这一变化过程中因变量是( )A、热水器里水的温度 B、太阳光的强弱 C、太阳光照射的时间 D、热水器的容积5. 下列算式能用平方差公式计算的是( )A、 B、 C、 D、6. 如图,将一副三角尺按不同位置摆放,摆放方式中的图形有( ) A、1个 B、2个 C、3个 D、4个7. 一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:
A、1个 B、2个 C、3个 D、4个7. 一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:支撑物的高度
10
20
30
40
50
60
70
小车下滑的时间
4.23
3.00
2.45
2.13
1.89
1.71
1.59
下列说法正确的是( )
A、t是自变量,h是因变量 B、h每增加 , t减小1.23 C、随着h逐渐变大,t也逐渐变大 D、随着h逐渐升高,小车下滑的平均速度逐渐加快8. 如图,河道的同侧有、两地,现要铺设一条引水管道,从地把河水引向、两地.下列四种方案中,最节省材料的是( )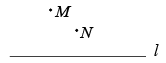 A、
A、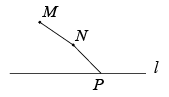 B、
B、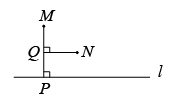 C、
C、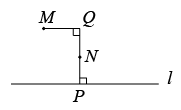 D、
D、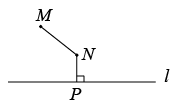 9. 如图所示的是超市里购物车的侧面示意图,扶手AB与车底CD平行, , ,则 的度数是( )
9. 如图所示的是超市里购物车的侧面示意图,扶手AB与车底CD平行, , ,则 的度数是( ) A、 B、 C、 D、10. 如图是两圆柱形连通容器,向甲容器匀速注水,则下面可以近似地刻画甲容器的水面高度随时间分的变化情况的是( )
A、 B、 C、 D、10. 如图是两圆柱形连通容器,向甲容器匀速注水,则下面可以近似地刻画甲容器的水面高度随时间分的变化情况的是( )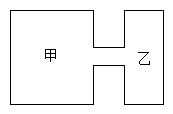 A、
A、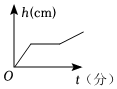 B、
B、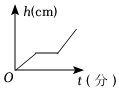 C、
C、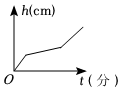 D、
D、
二、填空题
-
11. 计算: .12. 光在真空中的速度大约是 , 太阳系以外距离地球最近的恒星是比邻星,它发出的光到达地球大约需要年,一年以计算,则比邻星与地球的距离约为 .13. 科技小制作的特点在于富含科技,结构简单、材料好找、加工容易、能够独立完成,特别适合于学生.如图所示,某科技制作小组制作的一艘航模船从A点出发,沿东北方向航行至B点,再从B点出发沿南偏东15°方向航行至C点,则等于 .
 14. 某图书馆对外出租书的收费方式是:每本书出租后的前两天,每天收0.6元,以后每天收0.3元,那么一本书在出租后x()天后,所收租金y与天数x的表达式为 .15. 把一张长方形制片沿折叠后与的交点为 , 、分别在、的位置上,若 , 则 .
14. 某图书馆对外出租书的收费方式是:每本书出租后的前两天,每天收0.6元,以后每天收0.3元,那么一本书在出租后x()天后,所收租金y与天数x的表达式为 .15. 把一张长方形制片沿折叠后与的交点为 , 、分别在、的位置上,若 , 则 .
三、解答题
-
16. 计算:(1)、;(2)、;(3)、;(4)、(用乘法公式).17. 如图,已知 , 求作: , 使 . (要求:在指定作图区域用尺规作图,不写作法,保留作图痕迹)
 18. 下面是小李同学数学计算本上一道题的解答过程.请认真阅读并完成相应任务.
18. 下面是小李同学数学计算本上一道题的解答过程.请认真阅读并完成相应任务.第一步
第二步
第三步
(1)、任务一:第一步的计算过程中用到的乘法公式是;(2)、任务二:第步开始出现错误,这一步错误的原因是;(3)、任务三:请直接写出该题的正确运算结果:;(4)、任务四:除纠正上述错误外,请你根据平时的学习经验,就整式乘法运算时还需要注意的事项给其他同学提一条建议.19. 如图所示,小明家、食堂、图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如图反映了这个过程中,小明高家的距离y与时间x之间的对应关系.

根据图象回答下列问题:
(1)、食堂离小明家的距离是 , 小明从家到食堂用了分钟;(2)、小明吃早餐用了分钟,小明读报用了分钟;(3)、小明从图书馆回家的平均速度是多少?(4)、小明从家到食堂和从食堂到图书馆哪段距离走得快?20. 如图, , 的平分线交于点 , 交的延长线于点 , , 试说明 . 请将下面的说理过程补充完整:
解:(已知),
, ( )
平分 ,
▲ .(角平分线的定义)
. ( )
(已知),
▲ .( )
. ( )
. (等量代换)
21. 甲、乙两地打电话需付的电话费y(元)是随时间t(分钟)的变化而变化的,试根据下表列出的几组数据回答下列问题:通话时间t(分钟)
1
2
3
4
5
6
…
电话费y(元)
0.15
0.30
0.45
0.6
0.75
0.9
…
(1)、自变量是 , 因变量是(2)、写出电话费y(元)与通话时间t(分钟)之间的关系式;(3)、若小明通话15分钟,则需付话费多少元?(4)、若小明某次通话后,需付话费6元,则小明通话多少分钟?22. 图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形. (1)、你认为图b中的阴影部分的正方形的边长等于;(2)、观察图b,(2)请用两种不同的方法表示图中阴影部分的正方形的面积:
(1)、你认为图b中的阴影部分的正方形的边长等于;(2)、观察图b,(2)请用两种不同的方法表示图中阴影部分的正方形的面积:方法1:;方法2: .
(3)、你能写出下列三个代数式之间的等量关系吗?代数式: , ,
(4)、若 , , 请利用(3)中的结论,求的值.23. 综合与实践【问题情境】
在综合与实践课上,同学们以“一个含的直角三角尺和两条平行线”为背景开展数学活动.如图1,已知两直线a,b且和 , , , .
 (1)、在图1中, , 求的度数;(2)、 【深入探究】
(1)、在图1中, , 求的度数;(2)、 【深入探究】如图2,创新小组的同学把直线a向上平移,并把的位置改变,发现 , 请说明理由;
(3)、 【拓展应用】缜密小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,平分 , 此时发现与又存在新的数量关系,请直接写出与的数量关系.