山西省忻州地区2022-2023学年七年级下学期数学期中考试试卷

试卷更新日期：2023-06-25 类型：期中考试

进入出卷网下载

一、单选题

1. 9的平方根是（）

A、3 B、 $- 3$ C、 $\pm 3$ D、 $\pm \sqrt{3}$

查看试题解析
2. 如图，平行线 $A B$ ， $C D$ 被直线 $A E$ 所截， $∠ 1 = 70 °$ ，则 $∠ 2$ 的度数是（）

A、 $80 °$ B、 $90 °$ C、 $100 °$ D、 $110 °$

查看试题解析
3. 在实数 $\sqrt{3}$ ， $\sqrt[3]{- 8}$ ， $\frac{22}{7}$ ， $\frac{π}{3}$ ， $0.2020020002 ⋯$ (每两个相邻的2中间依次多一个0)中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列各组数中相等的是（　　）

A、-3与 $\sqrt{{(- 3)}^{2}}$ B、−2与 $\sqrt[3]{8}$ C、 $| - \sqrt{5} |$ 与 $\sqrt{5}$ D、−2与 $- \frac{1}{2}$

查看试题解析
5. 如图，从直线EF外一点P向EF引四条线段PA，PB，PC，PD，其中最短的是（）

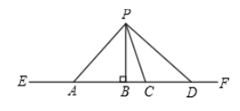A、PA B、PB C、PC D、PD

查看试题解析
6. 钓鱼岛及其附属岛屿自古以来就是中国的固有领土，在明代钓鱼岛纳入中国疆域版图，下列描述能够准确表示钓鱼岛地点的是（）

A、北纬 $25 ° 4 4^{'}$ B、福建的正东方向 C、距离温州市约356千米 D、北纬 $25 ° 44 . 1^{'}$ ，东经 $123 ° 27 . 5^{'}$

查看试题解析
7. 如图，将一张矩形纸片折叠成如图所示的形状，若 $∠ 1 = 30 °$ ，则 $∠ 2 =$ （）

A、 $135 °$ B、 $150 °$ C、 $105 °$ D、 $125 °$

查看试题解析
8. 点M在第二象限，距离x轴5个单位长度，距离y轴3个单位长度，则M点的坐标为（）

A、 $(- 5 ， 3)$ B、 $(5 ， - 3)$ C、 $(- 3 ， 5)$ D、 $(3 ， - 5)$

查看试题解析
9. 如图，直线a、b被直线c所截，则下列式子：① $∠ 1 = ∠ 8$ ；② $∠ 1 = ∠ 2$ ；③ $∠ 3 = ∠ 6$ ；④ $∠ 5 + ∠ 8 = 180 °$ ，能说明 $a ∥ b$ 的条件的是（　　）

A、①② B、②④ C、①②③ D、①②③④

查看试题解析
10. 如图，AF∥CD，CB平分∠ACD，BD平分∠EBF，且BC⊥BD，下列结论：① BC平分∠ABE；② AC∥BE；③ ∠CBE+∠D＝90°；④ ∠DEB＝2∠ABC.其中正确结论的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 比较大小：7 $\sqrt{50}$ （填“ $>$ ”、“ $<$ ”或“ $=$ ”）

查看试题解析
12. 将如图所示的“QQ”笑脸放置在3×3的正方形网格中，A、B、C三点均在格点上．若A、B的坐标分别为（－2，1），（－3，2），则点C的坐标为．

查看试题解析
13. 如图，计划把池中的水引到 $C$ 处，可过点 $C$ 作 $C D ⊥ A B$ ，垂足为点 $D$ ，然后沿 $C D$ 挖渠，可使所挖的渠道最短，这种设计的依据是．

查看试题解析
14. 若 $\sqrt{38.09}$ ≈6.172， $\sqrt{380.9}$ ≈19.517，则 $\sqrt{380900}$ ≈ ．

查看试题解析
15. 如图，直线 $A B$ 、 $C D$ 相交于点O， $O E$ 平分 $∠ B O D$ ， $O F$ 平分 $∠ C O E$ ．若 $∠ A O C$ 的度数为 $2 α$ ．则 $∠ E O F =$ ．（用含α的代数式表示）

查看试题解析

三、解答题

16. 计算：

(1)、 $\sqrt{{(- 5)}^{2}} + \sqrt[3]{- 27} - {(- 1)}^{2}$

(2)、 $- 2^{2} + \sqrt{16} - \sqrt[3]{8}$

(3)、 $\sqrt{3} (\sqrt{3} + \frac{1}{\sqrt{3}}) + \sqrt[3]{- 1}$

查看试题解析
17. 如甶，在平面直角坐标系中：

(1)、将 $△ A B C$ 向上平移3个单位，再向右平移2个单位得到 $△ A_{1} B_{1} C_{1}$ ，画出点A的对应点， $A_{1}$ 的坐标；并在坐标系中画出平移后的 $△ A_{1} B_{1} C_{1}$ ；

(2)、求 $△ A B C$ 的面积．

查看试题解析
18. 某地气象资料表明：某地雷雨持续的时间 $t (h)$ 可以用公式 $t = \sqrt{\frac{d^{2}}{900}}$ 来估计，其中 $d (k m)$ 是雷雨区域的直径.

(1)、如果雷雨区域的直径为 $8 k m$ ，那么这场雷雨大约能持续多长时间？

(2)、如果一场雷雨持续了 $2 h$ ，那么这场雷雨区域的直径大约是多少千米？

查看试题解析
19. 如图， $a ∥ b$ ， c，d是截线，已知 $∠ 1 = 80 °$ ， $∠ 5 = 105 °$ ，求 $∠ 2$ ， $∠ 3$ ， $∠ 4$ 的度数．

查看试题解析
20. 为了培养学生的爱国主义情怀，激发青少年报效祖国、奉献社会、服务人民的责任心和使命感，市教育局举办了“小小贺卡，军民情深”祝福活动．各学校积极响应组织开展手工绘制精美贺卡活动．小芳制作了一张面积为 $256 c m^{2}$ 的正方形贺卡．现有一个长方形信封如图所示，长、宽之比为 $3 ： 2$ ，面积为 $420 c m^{2}$ ，小芳能将这张贺卡不折叠就放入此信封吗？请通过计算说明你的判断．

查看试题解析
21. 如图，在 $△ A B C$ 中， $C F ⊥ A B$ 于 $F$ ， $E D ∥ C F$ ， $∠ 1 = ∠ 2$ ．

(1)、求证： $F G ∥ B C$ ；

(2)、若 $∠ A ＝ 60 °$ ， $∠ A G F ＝ 70 °$ ，求 $∠ B$ 及 $∠ 2$ 的度数．

查看试题解析
22. 阅读下面的文字，解答问题.
现规定：分别用 $[x]$ 和 $⟨ x ⟩$ 表示实数x的整数部分和小数部分，如实数 $3.14$ 的整数部分是 $[3.14] = 3$ ，小数部分是 $⟨ 3.14 ⟩ = 0.14$ ；实数 $\sqrt{7}$ 的整数部分是 $[\sqrt{7}] = 2$ ，小数部分是无限不循环小数，无法写完整，但是把它的整数部分减去，就等于它的小数部分，即 $\sqrt{7} - 2$ 就是 $\sqrt{7}$ 的小数部分，所以 $⟨ \sqrt{7} ⟩ = \sqrt{7} - 2$ .

(1)、 $[\sqrt{2}] =$ ， $⟨ \sqrt{2} ⟩ =$ ； $[\sqrt{11}] =$ ， $⟨ \sqrt{11} ⟩ =$ .

(2)、如果 $⟨ \sqrt{5} ⟩ = a$ ， $[\sqrt{101}] = b$ ，求 $a + b - \sqrt{5}$ 的立方根.

查看试题解析
23. 课题学习：平行线的“等角转化”功能．

(1)、阅读理解：如图1，已知点A是 $B C$ 外一点，连接 $A B$ 、 $A C$ ，求 $∠ B + ∠ B A C + ∠ C$ 的度数．阅读并补充下面推理过程．
解：过点A作 $E D ∥ B C$ ，

$∴$ $∠ B =$ ， $∠ C$ ，

$∵$ $∠ E A B + ∠ B A C + ∠ D A C = 180 °$ ，

$∴$ $∠ B + ∠ B A C + ∠ C = 180 °$ ．
解题反思：从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将 $∠ B A C$ 、 $∠ B$ 、 $∠ C$ “凑”在一起，得出角之间的关系，使问题得以解决．

(2)、方法运用：如图2，已知 $A B ∥ E D$ ，求 $∠ B + ∠ B C D + ∠ D$ 的度数；

(3)、深化拓展：已知 $A B ∥ C D$ ，点C在点D的右侧， $∠ A D C = 50 °$ ， $B E$ 平分 $∠ A B C$ ， $D E$ 平分 $∠ A D C$ ， $B E$ ， $D E$ 所在的直线交于点E，点E在直线 $A B$ 与 $C D$ 之间．
①如图3，点B在点A的左侧，若 $∠ A B C = 36 °$ ，求 $∠ B E D$ 的度数．

②如图4，点B在点A的右侧，且 $A B < C D$ ， $A D < B C$ ．若 $∠ A B C = n °$ ，求 $∠ B E D$ 度数．（用含n的代数式表示）

查看试题解析