天津市东丽区2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-06-25 类型:期中考试
一、单选题
-
1. 如图图形中∠1与∠2是对顶角的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列实数 , ,3.14159, ,0, +1,中无理数有( )A、0个 B、1个 C、2个 D、3个3. 如图,点E在射线上,要 , 只需( )
2. 下列实数 , ,3.14159, ,0, +1,中无理数有( )A、0个 B、1个 C、2个 D、3个3. 如图,点E在射线上,要 , 只需( ) A、 B、 C、 D、4. 已知点在轴的负半轴上,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列命题中,真命题的个数有( )
A、 B、 C、 D、4. 已知点在轴的负半轴上,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列命题中,真命题的个数有( )① 同一平面内,两条直线一定互
 相平行;② 有一条公共边的角叫邻补角;
相平行;② 有一条公共边的角叫邻补角;③ 内错角相等.④ 对顶角相等;
⑤ 从直线外一点到这条直线的垂线段,叫做点到直线的距离.
A、0个 B、1个 C、2个 D、3个6. 课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用(﹣2,0)表示,小军的位置用(0,1)表示,那么你的位置可以表示成( ) A、(2,3) B、(4,5) C、(3,2) D、(2,1)7. 如图,A,B的坐标为A,B(2,0),(0,1),若将线段AB平移至A1B1 , 点A对应点A1(3,b),点B对应点B1(a,3),则的值为( )
A、(2,3) B、(4,5) C、(3,2) D、(2,1)7. 如图,A,B的坐标为A,B(2,0),(0,1),若将线段AB平移至A1B1 , 点A对应点A1(3,b),点B对应点B1(a,3),则的值为( ) A、-1 B、1 C、3 D、58. 下列计算正确的是( )A、 =±3 B、 =﹣2 C、 =﹣3 D、9. 4的平方根是( )A、2 B、±2 C、 D、±10. 如图,某地域的江水经过B、C、D三点处拐弯后,水流的方向与原来相同,若∠ABC=125°,∠BCD=75°,则∠CDE的度数为( )
A、-1 B、1 C、3 D、58. 下列计算正确的是( )A、 =±3 B、 =﹣2 C、 =﹣3 D、9. 4的平方根是( )A、2 B、±2 C、 D、±10. 如图,某地域的江水经过B、C、D三点处拐弯后,水流的方向与原来相同,若∠ABC=125°,∠BCD=75°,则∠CDE的度数为( ) A、20° B、25° C、35° D、50°11. 若实数 , 满足 , 则的值为( )A、1 B、 C、2 D、12. 如图,把一张对边互相平行的纸条折叠,是折痕,若 , 下列结论:①;②;③;④ , 其中正确的有( )
A、20° B、25° C、35° D、50°11. 若实数 , 满足 , 则的值为( )A、1 B、 C、2 D、12. 如图,把一张对边互相平行的纸条折叠,是折痕,若 , 下列结论:①;②;③;④ , 其中正确的有( )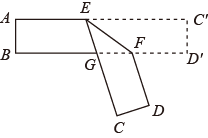 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 的算术平方根是 .14. 如图,沿所在直线向右平移得到 , 已知 , , 则平移的距离为 .
 15. 如图,将一块三角板的直角顶点放在直尺的一边上,当 时, .
15. 如图,将一块三角板的直角顶点放在直尺的一边上,当 时, .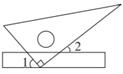 16. 点P(2,-5)关于y轴对称的点的坐标为 .17. 已知≈1.038,≈2.237,≈4.820,则≈ .18. 如图,数轴上 , 两点表示的数分别为和4.1,则 , 两点之间表示整数的点共有个.
16. 点P(2,-5)关于y轴对称的点的坐标为 .17. 已知≈1.038,≈2.237,≈4.820,则≈ .18. 如图,数轴上 , 两点表示的数分别为和4.1,则 , 两点之间表示整数的点共有个.
三、解答题
-
19. 计算:(1)、;(2)、 .20. 已知点 , 解答下列各题:(1)、若点P在x轴上,则点P的坐标为 ;(2)、若 , 且轴,则点P的坐标为 ;(3)、若点P在第二象限,且它到x轴、y轴的距离相等,求的值.21. 如图,已知∠1=38°,∠2=38°,∠3=115°36′.求∠4的度数.
 22. 已知一个正数的两个不同的平方根是 和 的立方根为(1)、求 的值(2)、求 的平方根23. 已知:如图,∠1和∠2互为补角,∠A=∠D,求证AB∥CD.
22. 已知一个正数的两个不同的平方根是 和 的立方根为(1)、求 的值(2)、求 的平方根23. 已知:如图,∠1和∠2互为补角,∠A=∠D,求证AB∥CD. 24. 如图,先将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A1B1C1 .
24. 如图,先将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A1B1C1 .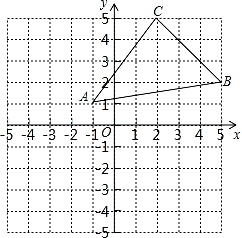 (1)、画出经过两次平移后的图形,并写出A1、B1、C1的坐标;(2)、已知三角形ABC内部一点P的坐标为(a,b),若点P随三角形ABC一起平移,平移后点P的对应点P1的坐标为(﹣2,﹣2),请求出a,b的值;(3)、求三角形ABC的面积.25. 【阅读材料】
(1)、画出经过两次平移后的图形,并写出A1、B1、C1的坐标;(2)、已知三角形ABC内部一点P的坐标为(a,b),若点P随三角形ABC一起平移,平移后点P的对应点P1的坐标为(﹣2,﹣2),请求出a,b的值;(3)、求三角形ABC的面积.25. 【阅读材料】在“相交线与平行线”的学习中,有这样一道典型问题:
如图①,AB∥CD,点P在AB与CD之间,可得结论:∠BAP+∠APC+∠PCD=360°.

理由如下:
过点P作PQ∥AB.
∴∠BAP+∠APQ=180°.
∵AB∥CD,
∴PQ∥CD.
∴∠PCD+∠CPQ=180°.
∴∠BAP+∠APC+∠PCD
=∠BAP+∠APQ+∠CPQ+∠PCD
=180°+180°
=360°.

【问题解决】
(1)、如图②,AB∥CD,点P在AB与CD之间,写出∠BAP,∠APC,∠PCD间的等量关系;(只写结论)(2)、如图③,AB∥CD,点P,E在AB与CD之间,AE平分∠BAP,CE平分∠DCP.写出∠AEC与∠APC间的等量关系,并说明理由;(3)、如图④,AB∥CD,点P,E在AB与CD之间,∠BAE=∠BAP,∠DCE=∠DCP,写出∠AEC与∠APC间的等量关系.(只写结论)