天津市南开区2022-2023学年七年级下学期数学期中考试试卷
试卷更新日期:2023-06-25 类型:期中考试
一、单选题
-
1. 图中所示的图案通过平移后得到的图案是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 估计 的值应在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间3. 课间操时,小华、小军、小刚的位置如图.小华对小刚说:“如果我的位置用表示,小军的位置用表示,那么你的位置可以表示成( )
2. 估计 的值应在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间3. 课间操时,小华、小军、小刚的位置如图.小华对小刚说:“如果我的位置用表示,小军的位置用表示,那么你的位置可以表示成( )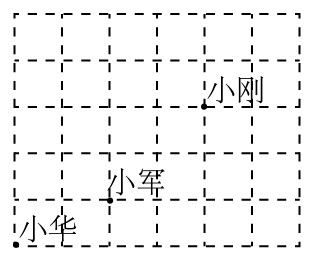 A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 在下面四个点中,位于第二象限的点是( )A、 B、 C、 D、6. 如图,点在直线外,点、在直线上,若 , , 则点到直线的距离可能是( )
A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 在下面四个点中,位于第二象限的点是( )A、 B、 C、 D、6. 如图,点在直线外,点、在直线上,若 , , 则点到直线的距离可能是( ) A、 B、 C、 D、7. 由可以得到用x表示y的式子为( )A、 B、 C、 D、8. 如图,下列条件中,不能判断的是( )
A、 B、 C、 D、7. 由可以得到用x表示y的式子为( )A、 B、 C、 D、8. 如图,下列条件中,不能判断的是( ) A、 B、 C、 D、9. 平面直角坐标系中,点 , 点 , 轴,则的值为( )A、2 B、5 C、8 D、1110. 如图,点B,C,D在一条直线上, , 的面积为12,则的面积为( )
A、 B、 C、 D、9. 平面直角坐标系中,点 , 点 , 轴,则的值为( )A、2 B、5 C、8 D、1110. 如图,点B,C,D在一条直线上, , 的面积为12,则的面积为( )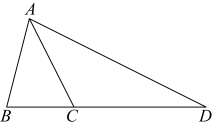 A、6 B、12 C、18 D、2411. 下列命题为真命题的是( )A、邻补角的角平分线互相垂直 B、两条直线被第三条直线所截,同位角相等 C、相等的角是对顶角 D、互补的两个角的角平分线互相垂直12. 在平面直角坐标系中有 , , 三点,且点 , 点 , 点 , 若的立方根是 , 的算术平方根为 , 是比小的最大整数,则下列结论:
A、6 B、12 C、18 D、2411. 下列命题为真命题的是( )A、邻补角的角平分线互相垂直 B、两条直线被第三条直线所截,同位角相等 C、相等的角是对顶角 D、互补的两个角的角平分线互相垂直12. 在平面直角坐标系中有 , , 三点,且点 , 点 , 点 , 若的立方根是 , 的算术平方根为 , 是比小的最大整数,则下列结论:①;
②的平方根为;
③;
④c是关于的方程的解;
⑤若线段 , 且 , 则点的坐标为或 .
其中正确的个数有( )
A、5个 B、4个 C、3个 D、2个二、填空题
-
13. 4是 的算术平方根.14. 若 , 则的值为 .15. 若一个数的立方根等于它的平方根,则这个数是 .16. 如图,已知 , , , 则度.
 17. 在平面直角坐标系中,如果点在x轴的负半轴上,则A的坐标为 .18. 已知 ∠1的两边分别平行于 ∠2 的两边,若 ∠1 = 40°,则 ∠2 的度数为 .
17. 在平面直角坐标系中,如果点在x轴的负半轴上,则A的坐标为 .18. 已知 ∠1的两边分别平行于 ∠2 的两边,若 ∠1 = 40°,则 ∠2 的度数为 .三、解答题
-
19. 计算:(1)、;(2)、 .20. 求下列各式中的值.(1)、;(2)、 .21. 解下列方程组:(1)、;(2)、 .22. 完成下面的证明.
如图,点 , , 在一条直线上,点 , , 在一条直线上,连接 , , , 分别交 , 于点 , , , .
求证: .
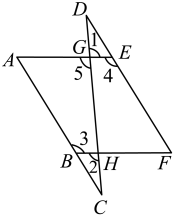
证明:( ),
又(已知),
▲ = ▲ (等量代换),
▲ ▲ ( ),
▲ ( ),
又(已知),
(等量代换),
▲ ▲ ( ),
( ).
23. 如图,点 , 点 , 点 , 点 . 将四边形向右平移个单位长度,再向上平移个单位长度,得到四边形 .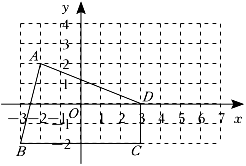 (1)、画出经过两次平移后的图形,并写出点的坐标;(2)、已知四边形内部一点随四边形一起平移,经过两次平移后点的对应点的坐标为 , 请求出点的坐标;(3)、求四边形的面积.24. 如图1,直线与直线分别交于点E,F,与互补.
(1)、画出经过两次平移后的图形,并写出点的坐标;(2)、已知四边形内部一点随四边形一起平移,经过两次平移后点的对应点的坐标为 , 请求出点的坐标;(3)、求四边形的面积.24. 如图1,直线与直线分别交于点E,F,与互补. (1)、试判断直线与直线的位置关系,并说明理由;(2)、如图2,与的角平分线交于点P,与交于点G,点H是上一点,且于点G,求证:;(3)、如图3,在(2)的条件下,连接 , I是上一点使 , 作平分 , 问的大小是否发生变化?若不变,请求出其值;若变化,说明理由.
(1)、试判断直线与直线的位置关系,并说明理由;(2)、如图2,与的角平分线交于点P,与交于点G,点H是上一点,且于点G,求证:;(3)、如图3,在(2)的条件下,连接 , I是上一点使 , 作平分 , 问的大小是否发生变化?若不变,请求出其值;若变化,说明理由.