沪科版数学七年级下册相交线平行线性质综合应用（含角度问题）

试卷更新日期：2023-06-22 类型：同步测试

进入 出卷网 下载

一、综合题

  • 1. 如图1，已知AB//CD，点G在AB上，点H在EF上，连接CG、CH ， CG⊥CH ， ∠CHE+∠CGA=90° ．

    (1)、求证：AB//EF；
    (2)、如图2，若∠BAE=90° ， 延长HC交BA的延长线于点M，请直接写出图2中所有与∠AGC互余的角．

    查看试题解析

  • 2. 如图，直线AB∥CD ， 点E，G在直线AB上，点F，H在直线CD上，∠1＋∠2＝180°．

    (1)、如图1，求证：EF∥GH；
    (2)、如图2，若∠1＝120°，GM平分∠BGH，FM平分∠EFH，设FM与GH相交于点O．求∠FOH的度数．

    查看试题解析

  • 3. 如图1，在四边形ABCD中，AB//DC ， AD//BC ， 点E在AB边上，DE平分∠ADC ．

    (1)、如图1，分别延长DE、CB交于点M ， 分别作∠DAB与∠CMD的平分线AN、MN交于点N ， 请根据题意补全图形．

    ①若∠ADE的度数为56°，求∠N的度数；

    ②试探究∠ADE和∠N的数量关系，并直接写出结论；

    (2)、如图2，已知DF⊥BC交BC边于点G ， 交AB边的延长线于点F ， 且DB平分∠EDF ， 若∠BDC<45° ， 试比较∠F与∠EDF的大小，并说明理由．

    查看试题解析

  • 4. 平面内的两条直线有相交和平行两种位置关系，AB∥CD如图，点P在AB、CD外部时，由AB∥CD ， 有∠B=∠BOD，因∠BOD+∠POD=180°，∠POD +∠BPD+∠D =180°，故∠BOD=∠BPD +∠D，得∠BPD=∠B-∠D．

    (1)、如图，将点P移到AB、CD内部，延长BP交CD于点E，以上结论是否成立？若不成立，则∠BPD、∠B、∠D之间有何数量关系？请说明你的理由；

    (2)、如图，直线AB与直线CD交于点Q，延长BP交CD于点F，则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系？（不需说明理由）；

    (3)、若∠A=60°，∠B=15°，∠E=20°，根据（2）的结论求图中∠AGB的度数．

    查看试题解析

  • 5. 已知直线EF分别与直线AB，CD相交于点G，M，并且∠AGE+∠CHF=180°．

     

    (1)、如图1，求证：AB∥CD；
    (2)、如图2，点Ｍ在直线AB，CD之间，连接GM，HM，求证：∠GMH=∠AGM+∠CHM；
    (3)、如图3，在（2）的条件下，若射线GH恰好是∠BGM的平分线，在MH的延长线上取点N，连接GN，若∠N=∠AGM，∠GMH=∠N+12∠FGN ， 则∠M、∠N、∠FGN的数量关系是（直接写答案）

    查看试题解析

  • 6. 探索发现：
    (1)、如图1，AB∥CD ， 小明同学通过过点E作AB的平行线，利用平行线的性质，得出了∠ABE，∠BED，∠CDE之间的关系，请你猜测∠ABE，∠BED，∠CDE之间的关系；
    (2)、
    变式迁移：
    如图2，AB∥CD ， 试探究∠ABE，∠BED，∠CDE之间的关系；
    (3)、如图3，AB∥CD ， DE平分∠CDF，BF⊥BE ， 若∠ABE=50° ， ∠BED=80° ， 求∠BFD的度数．

    查看试题解析

  • 7. 如图1，将一副三角板中的两个直角顶点C叠放在一起，其中∠A=30° ， ∠B=60° ， ∠D=∠E=45°.

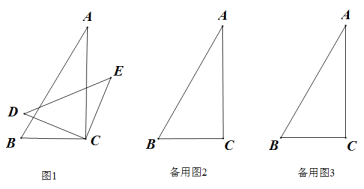    (1)、观察猜想，∠BCD与∠ACE的数量关系是；∠BCE与∠ACD的数量关系是；
    (2)、类比探究，若按住三角板ABC不动，顺时针绕直角顶点C转动三角形DCE ， 试探究当∠ACD等于多少度时CE//AB，画出图形并简要说明理由；
    (3)、拓展应用，若∠BCE＝3∠ACD，求∠ACD的度数；并直接写出此时DE与AC的位置关系.

    查看试题解析

  • 8. 在综合与实践课上，老师让同学们以“两条平行线AB ， CD和一块含60°角的直角三角尺EFG(∠EFG=90° ， ∠EGF=60°)”为主题开展数学活动.

    (1)、如图1，若三角尺的60°角的顶点G放在CD上，若∠2=2∠1 ， 求∠1的度数；
    (2)、如图2，小颓把三角尺的两个锐角的顶点E，G分别放在AB和CD上，请你探案并说明∠AEF与∠FGC间的数量关系；
    (3)、如图3，小亮把三角尺的直角顶点F放在CD上，30°角的顶点E落在AB上.若∠AEG=α ， ∠CFG=β ， 则∠AEG与∠CFG的数量关系是什么？用含α ， β的式子表示并说明理由.

    查看试题解析

  • 9. 如图，点A ， B ， C ， D四点共线，点E ， F ， G ， H四点共线．BG ， CF相交于点I ， 点J是直线AD与EH之间的一个动点，∠ABJ+∠J+∠EFJ=360° ．

    (1)、求证：AD∥EH；
    (2)、若BJ平分∠DBG ， FJ平分∠CFH ， 请探索并证明∠BIF和∠BJF之间的数量关系；
    (3)、若∠GBJ=13∠GBD ， ∠CFJ=13∠CFH ， （2）中的结论还成立吗？若成立请证明；若不成立，请写出你认为正确的结论，并证明．

    查看试题解析

  • 10. 如图1，MN∥EF ， C为两直线之间一点．

    (1)、如图1，若∠MAC与∠EBC的平分线相交于点D，若∠ACB=100° ， 求∠ADB的度数．
    (2)、如图2，若∠CAM与∠CBE的平分线相交于点D，∠ACB与∠ADB有何数量关系？并证明你的结论．
    (3)、如图3，若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D，请直接写出∠ACB与∠ADB之间的数量关系： ．

    查看试题解析

  • 11. 在一次数学综合实践活动课上，同学们进行了如下探究活动：将一块等腰直角三角板GEF的顶点G放置在直线AB上，旋转三角板．

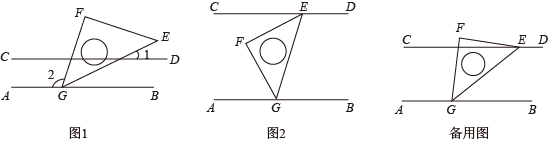    (1)、如图1，在GE边上任取一点P（不同于点G，E），过点P作CD∥AB ， 若∠1=27° ， 求∠2的度数；
    (2)、如图2，过点E作CD∥AB ， 请探索并说明∠AGF与∠CEF之间的数量关系；
    (3)、将三角板绕顶点G转动，过点E作CD∥AB ， 并保持点E在直线AB的上方．在旋转过程中，探索∠AGF与∠CEF之间的数量关系，并说明理由．

    查看试题解析

  • 12. 如图1，点E、F分别在直线AB、CD上，点P为AB、CD之间的一点，且∠AEP+∠EPF+∠PFC=360° ．

    (1)、求证：AB∥CD；
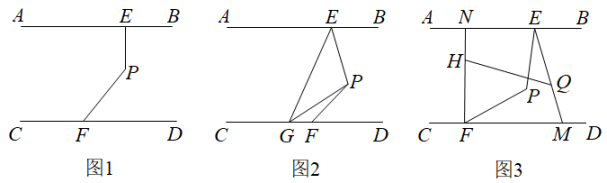    (2)、如图2，点G在射线FC上，PG平分∠EGF ， ∠PFD=∠PEG ， 探究∠EPF与∠PGF之间的数量关系．并说明理由；
    (3)、如图3，∠BEM=2∠PEM ， ∠CFN=2∠PFN ． 直线HQ分别交FN，EM于H、Q两点，若∠EPF=150° ， 求∠FHQ−∠HQE的度数．

    查看试题解析

  • 13. 阅读理解：如图1 ， 已知点A是BC外一点，连接AB ， AC.求∠BAC+∠B+∠C的度数．

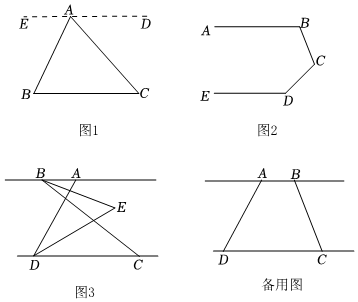    (1)、阅读并补充下面推理过程．

    解：过点A作ED//BC ， ∴∠B= ， ∠C= ．

    ∵∠EAB+∠BAC+∠DAC=180° ．

    ∴∠B+∠BAC+∠C=180° ．

    解题反思：从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将∠BAC ， ∠B ， ∠C“凑”在一起，得出角之间的关系，使问题得以解决．

    (2)、方法运用：如图2，已知AB//ED ， 求∠B+∠BCD+∠D的度数．
    (3)、深化拓展：如图3，已知AB//CD ， 点C在点D的右侧，∠ADC=60° ， DE平分∠ADC ， 点B是直线AB上的一个动点（不与点A重合），AB<CD ， BE平分∠ABC ， BE ， DE所在的直线交于点E ， 点E在AB与CD两条平行线之间．若∠ABC=n° ， 请你直接写出∠BED的度数．（用含n的代数式表示）.

    查看试题解析