四川省雅安市2022-2023学年高三理数第三次模拟考试试卷
试卷更新日期:2023-06-21 类型:高考模拟
一、单选题
-
1. 设集合或 , , 则集合( )A、 B、 C、 D、2. 在复平面内,复数对应的点的坐标是 , 则的共轭复数为( )A、 B、 C、 D、3. 利用独立性检验来考查两个分类变量和是否有关系时,通过查阅下表来确定“和有关系”的可信度.如果 , 那么就有把握认为“和有关系”的百分比为( )A、25% B、75% C、2.5% D、97.5%4. 日光射入海水后,一部分被海水吸收(变为热能),同时,另一部分被海水中的有机物和无机物有选择性地吸收与散射.因而海水中的光照强度随着深度增加而减弱,可用表示其总衰减规律,其中是平均消光系数(也称衰减系数),(单位:米)是海水深度,(单位:坎德拉)和(单位:坎德拉)分别表示在深度处和海面的光强.已知某海区10米深处的光强是海面光强的 , 则该海区消光系数的值约为( )(参考数据: , )A、0.12 B、0.11 C、0.07 D、0.015. 一个正三棱柱(底面为正三角形的直棱柱)的三视图如图所示,则这个正三棱柱的外接球的表面积为( )
 A、 B、 C、 D、6. 智慧的人们在进行工业设计时,巧妙地利用了圆锥曲线的光学性质,比如电影放映机利用椭圆镜面反射出聚焦光线,探照灯利用抛物线镜面反射出平行光线.如图,从双曲线右焦点发出的光线通过双曲线镜面反射,且反射光线的反向延长线经过左焦点 . 已知入射光线斜率为 , 且和反射光线PE互相垂直(其中P为入射点),则双曲线的离心率为( )
A、 B、 C、 D、6. 智慧的人们在进行工业设计时,巧妙地利用了圆锥曲线的光学性质,比如电影放映机利用椭圆镜面反射出聚焦光线,探照灯利用抛物线镜面反射出平行光线.如图,从双曲线右焦点发出的光线通过双曲线镜面反射,且反射光线的反向延长线经过左焦点 . 已知入射光线斜率为 , 且和反射光线PE互相垂直(其中P为入射点),则双曲线的离心率为( ) A、 B、 C、 D、7. 在等比数列 中,和是方程的两根,则( )A、3 B、5 C、-1 D、8. 的内角 , , 所对的边分别为 , , 已知 , , 则( )A、 B、 C、 D、9. 将函数图象上所有点的横坐标伸长到原来的2倍,再向右平移个单位长度,得到函数的图象,若为奇函数,则ω的最小值为( )A、4 B、3 C、2 D、110. 某高校组织大学生知识竞赛,共设有5个版块的试题,分别是“中华古诗词”“社会主义核心价值观”“科学实践观”“中国近代史”及“创新发展能力”.某参赛队从中任选2个版块作答,则“创新发展能力”版块被该队选中的概率为( )A、 B、 C、 D、11. 在数学探究活动课中,小华进行了如下探究:如图1,水平放置的正方体容器中注入了一定量的水;现将该正方体容器其中一个顶点固定在地面上,使得DA,DB,DC三条棱与水平面所成角均相等,此时水平面为HJK,如图2所示.若在图2中 , 则在图1中( )
A、 B、 C、 D、7. 在等比数列 中,和是方程的两根,则( )A、3 B、5 C、-1 D、8. 的内角 , , 所对的边分别为 , , 已知 , , 则( )A、 B、 C、 D、9. 将函数图象上所有点的横坐标伸长到原来的2倍,再向右平移个单位长度,得到函数的图象,若为奇函数,则ω的最小值为( )A、4 B、3 C、2 D、110. 某高校组织大学生知识竞赛,共设有5个版块的试题,分别是“中华古诗词”“社会主义核心价值观”“科学实践观”“中国近代史”及“创新发展能力”.某参赛队从中任选2个版块作答,则“创新发展能力”版块被该队选中的概率为( )A、 B、 C、 D、11. 在数学探究活动课中,小华进行了如下探究:如图1,水平放置的正方体容器中注入了一定量的水;现将该正方体容器其中一个顶点固定在地面上,使得DA,DB,DC三条棱与水平面所成角均相等,此时水平面为HJK,如图2所示.若在图2中 , 则在图1中( )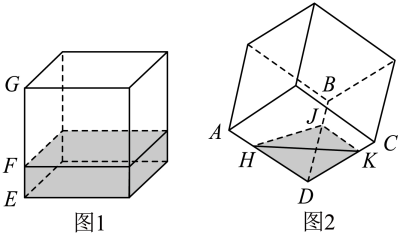 A、 B、 C、 D、12. 已知 , 则( )A、 B、 C、 D、
A、 B、 C、 D、12. 已知 , 则( )A、 B、 C、 D、二、填空题
-
13. 在的展开式中的系数为.14. 若向量满足 , 则.15. 已知函数是定义域为R的偶函数,当时, , 若关于x的方程有且仅有7个不同实数根,则.16. 比利时数学家丹德林发现:在圆锥内放两个大小不同且不相切的球,使得它们分别与圆锥的侧面、底面相切,用与两球都相切的平面截圆锥的侧面得到的截面曲线是椭圆.这个结论在圆柱中也适用,如图所示,在一个高为 , 底面半径为的圆柱体内放两个球,球与圆柱底面及侧面均相切.若一个平面与两个球均相切,则此平面截圆柱边缘所得的图形为一个椭圆,该椭圆的离心率为.

三、解答题
-
17. 成都是全国闻名的旅游城市,有许多很有特色的旅游景区某景区为了提升服务品质,对过去天每天的游客数进行了统计分析,发现这天每天的游客数都没有超出八千人,统计结果见下面的频率分布直方图:

为了研究每天的游客数是否和当天的最高气温有关,从这一百天中随机抽取了天,统计出这天的游客数千人分别为、、、、 , 已知这天的最高气温依次为、、、、 .
参考公式:由最小二乘法所得回归直线的方程是;其中: , .
本题参考数据: , .
(1)、根据以上数据,求游客数关于当天最高气温的线性回归方程系数保留一位小数;(2)、根据(1)中的回归方程,估计该景区这天中最高气温在内的天数保留整数18. 已知数列的前项和为 , 且 , ____.请在①;②成等比数列;③ , 这三个条件中任选一个补充在上面题干中,并解答下面问题.(1)、求数列的通项公式;(2)、若 , 记数列的前项和为 , 求证: .19. 如图,在多面体ABCDEF中,四边形ABCD与ABEF均为直角梯形,平面平面ABEF, . (1)、已知点G为AF上一点,且AG=1,求证:平面DCE;(2)、已知直线BF与平面DCE所成角的正弦值为 , 求平面DCE与平面BDF所成锐二面角的余弦值.20. 已知椭圆 , 离心率为分别为椭圆的左、右顶点,过焦点且垂直于轴的直线被椭圆截得的线段长为3.(1)、求椭圆的标准方程.(2)、当直线过椭圆的左焦点以及上顶点时,直线与椭圆交于另一点 , 求此时的弦长.(3)、设直线过点 , 且与轴垂直,为直线上关于轴对称的两点,直线与椭圆相交于异于的点 , 直线与轴的交点为 , 当与的面积之差取得最大值时,求直线的方程.
(1)、已知点G为AF上一点,且AG=1,求证:平面DCE;(2)、已知直线BF与平面DCE所成角的正弦值为 , 求平面DCE与平面BDF所成锐二面角的余弦值.20. 已知椭圆 , 离心率为分别为椭圆的左、右顶点,过焦点且垂直于轴的直线被椭圆截得的线段长为3.(1)、求椭圆的标准方程.(2)、当直线过椭圆的左焦点以及上顶点时,直线与椭圆交于另一点 , 求此时的弦长.(3)、设直线过点 , 且与轴垂直,为直线上关于轴对称的两点,直线与椭圆相交于异于的点 , 直线与轴的交点为 , 当与的面积之差取得最大值时,求直线的方程.