上海市重点大学附中2023届高三年级数学毕业考试试卷
试卷更新日期:2023-06-21 类型:高考模拟
一、填空题
-
1. 已知集合 中的最大元素为2, 则实数 .2. 函数 的严格减区间为.3. 若函数 为偶函数, 且当 时, , 则 .4. 若某圆锥高为3 , 其侧面积与底面积之比为 , 则该圆锥的体积为.5. 已知样本数据 2、4、8、 的极差为 10 , 其中 , 则该组数据的方差为.6. 在财务审计中, 我们可以用 “本・福特定律” 来检验数据是否造假. 本・福特定律指出, 在一组没有人为编造的自然生成的数据 (均为正实数) 中, 首位非零的数字是 这九个事件不是等可能的. 具体来说, 随机变量 是一组没有人为编造的首位非零数字,
则 . 则根据本 • 福特定律, 首位非零数字是1与首位非零数字是8的概率之比约为 (保留至整数).
7. 若 , 则 .8. 若向量 与 不共线也不垂直, 且 , 则向量夹角 .9. 已知复数 在复平面内对应的点是 , 其共轭复数 在复平面内对应的点是 是坐标原点, 若 在第一象限, 且 , 则 .10. 已知双曲线 的左、右焦点分别为 、 的渐近线与圆 在第一象限的交点为 , 线段 与 交于点 为坐标原点. 若 , 则 的离心率为.11. 若项数为10的数列 , 满足 , 且 , 则数列 中最大项的最大值为.12. 若实数 使得存在两两不同的实数 , 有 , 则实数 的取值范围是.二、选择题
-
13. 我国古代数学著作《九章算术》中有如下问题: “今有善走男, 日增等里, 首日行走一百里, 九日共行一千二百六十里, 问日增几何?", 该问题中, “善走男” 第5日所走的路程里数为 ( )A、110 B、120 C、130 D、14014. “ 表示焦点在 轴上的椭圆” 的一个充分非必要条件是 ( )A、 B、 C、 D、15. 若干个能确定一个立体图形的体积的量称为该立体图形的“基本量”, 已知长方体 ,下列四组量中, 一定能成为该长方体的 “基本量” 的是( )
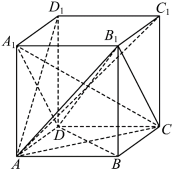 A、 、 、 的长度 B、 、 、 的长度 C、 、 、 的长度 D、 、 、 的长度16. 设关于 、 的表达式 , 当 、 取遍所有实数时, ( )A、既有最大值, 也有最小值 B、有最大值,无最小值 C、无最大值,有最小值 D、既无最大值, 也无最小值
A、 、 、 的长度 B、 、 、 的长度 C、 、 、 的长度 D、 、 、 的长度16. 设关于 、 的表达式 , 当 、 取遍所有实数时, ( )A、既有最大值, 也有最小值 B、有最大值,无最小值 C、无最大值,有最小值 D、既无最大值, 也无最小值三、解答题
-
17. 在平面直角坐标系 中, 在以原点 为圆心半径等1的圆上,将射线 绕原点 逆时针方向旋转 后交该圆于点 ,设点 的横坐标为 ,纵坐标 .
 (1)、如果 , ,求 的值(用 表示);(2)、如果 ,求 的值.18. 如图,矩形AMND所在平面与直角梯形MBCN所在的平面垂直,MB//NC,MN⊥MB.
(1)、如果 , ,求 的值(用 表示);(2)、如果 ,求 的值.18. 如图,矩形AMND所在平面与直角梯形MBCN所在的平面垂直,MB//NC,MN⊥MB. (1)、求证:平面AMB//平面DNC;(2)、若MC⊥CB,求证:BC⊥AC.19. 某科技公司为确定下一年度投入某种产品的研发费,需了解年研发费x(单位:万元)对年销售量y(单位:百件)和年利润(单位:万元)的影响,现对近6年的年研发费 和年销售量 ( ,2,…,6)数据作了初步处理,得到下面的散点图及一些统计量的值.
(1)、求证:平面AMB//平面DNC;(2)、若MC⊥CB,求证:BC⊥AC.19. 某科技公司为确定下一年度投入某种产品的研发费,需了解年研发费x(单位:万元)对年销售量y(单位:百件)和年利润(单位:万元)的影响,现对近6年的年研发费 和年销售量 ( ,2,…,6)数据作了初步处理,得到下面的散点图及一些统计量的值.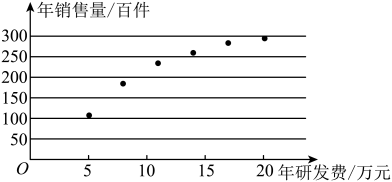
12.5
222
3.5
157.5
16800
4.5
1254
270
表中 , .
(1)、根据散点图判断 与 哪一个更适宜作为年研发费x的回归方程类型;(给出判断即可,不必说明理由)(2)、根据(1)的判断结果及表中数据,建立y关于x的回归方程;(3)、已知这种产品的年利润 ,根据(2)的结果,当年研发费为多少时,年利润z的预报值最大?附:对于一组数据 , ,…, ,其回归直线 的斜率和截距的最小二乘估计分别为 , .20. 贝塞尔曲线是计算机图形学和相关领域中重要的参数曲线.法国数学象卡斯特利奥对贝塞尔曲线进行了图形化应用的测试,提出了De Casteljau算法:已知三个定点,根据对应的比例,使用递推画法,可以画出地物线.反之,已知抛物线上三点的切线,也有相应成比例的结论.如图所示,抛物线 ,其中 为一给定的实数..
 (1)、写出抛物线 的焦点坐标及准线方程;(2)、若直线 与抛物线只有一个公共点,求实数k的值;(3)、如图,A,B,C是H上不同的三点,过三点的三条切线分别两两交于点D,E,F,
(1)、写出抛物线 的焦点坐标及准线方程;(2)、若直线 与抛物线只有一个公共点,求实数k的值;(3)、如图,A,B,C是H上不同的三点,过三点的三条切线分别两两交于点D,E,F,证明: .
21. 设 是定义域为 的函数,如果对任意的 、 均成立, 则称 是“平缓函数”.(1)、若 , 试判断 和 是否为“平缓函数” ?并说明理由; (参考公式: 时, 恒成立)
(2)、若函数 是“平缓函数”, 且 是以 1为周期的周期函数,证明:对任意的 、 , 均有 ;
(3)、设 为定义在 上函数, 且存在正常数 使得函数 为“平缓函数”.现定义数列 满足: ,
试证明:对任意的正整数 .