河北省衡水市三校联考2023年中考二模数学试题

试卷更新日期：2023-06-21 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，围绕在正方形四周的四条线段a，b，c，d中，长度最小的是（　　）

A、a B、b C、c D、d

查看试题解析
2. 下列各式的值最小的是（）

A、 $- \frac{1}{2} - 1$ B、 $- \frac{1}{2} + 1$ C、 $\frac{1}{2} - 1$ D、 $\frac{1}{2} + 1$

查看试题解析
3. 已知 $- 3 a < - 3 b$ ，则a和b的关系是（）

A、 $a < b$ B、 $a > b$ C、 $a \leq b$ D、不能确定

查看试题解析
4. 如图是嘉嘉把纸折叠后剪出的图案，将剪纸展开后得到的图案是（　　）

A、 B、 C、 D、

查看试题解析
5. 互联网已经进入 $5 G$ 时代，应用 $5 G$ 网络下载一个 $1000 K B$ 的文件只需要 $0.00076$ 秒，将数据 $0.00076$ 用科学记数法表示应为（）

A、 $76 \times 1 0^{- 3}$ B、 $7.6 \times 1 0^{- 3}$ C、 $7.6 \times 1 0^{- 4}$ D、 $7.6 \times 1 0^{- 5}$

查看试题解析
6. 如图，点P为观测站，一艘巡航船位于观测站P的南偏西 $34 °$ 方向的点A处，一艘渔船在观测站P的南偏东 $56 °$ 方向的点B处，巡航船和渔船与观测站P的距离分别为45海里、60海里．现渔船发生紧急情况无法移动，巡航船以30海里/小时的速度前去救助，至少需要的时间是（）

A、 $1.5$ 小时 B、2小时 C、 $2.5$ 小时 D、4小时

查看试题解析
7. 数学课上进行小组合作式学习，老师让小组成员的2号同学写出5个常错的式子，4号同学进行判断，则判断正确的个数是（　　）
（1） ${(- a^{3})}^{2} = {(- a^{2})}^{3}$ （×）
（2） $a^{3} - a^{2} ＝ a$ （×）
（3） $a^{6} \div a^{2} ＝ a^{3}$ （×）
（4） $3 a^{2} - (- a^{2}) ＝ 2 a^{2}$ （√）
（5） $a^{4} ・ a^{2} ＝ a^{8}$ （×）

A、5个 B、4个 C、3个 D、2个

查看试题解析
8. 如图，将一个无盖正方体盒子展开成平面图形的过程中，需要剪开的棱的条数是（）

A、2条 B、3条 C、4条 D、5条

查看试题解析
9. 定理：三角形的内角和是180°．
已知： $∠ C E D 、 ∠ C 、 ∠ D$ 是 $△ C E D$ 的三个内角．

求证： $∠ C + ∠ D + ∠ C E D ＝ 180 °$ ．

有如下四个说法：①*表示内错角相等，两直线平行；②@表示 $∠ B E C$ ；③上述证明得到的结论，只有在锐角三角形中才适用；④上述证明得到的结论，适用于任何三角形．其中正确的是（　　）

证明：如图，过点E作直线 $A B$ ，

使得 $A B ∥ C D$ ，

∴ $∠ 2 ＝ ∠ D$ （*），

$∠ 1 + ∠ @ ＝ 180 °$ ，

∴ $∠ C + ∠ D + ∠ C E D ＝ 180 °$ ．

A、①② B、②③ C、②④ D、①③

查看试题解析
10. 甲、乙两名队员参加射击训练（各射击10次），将训练成绩分别制成下列两个统计图（如图1、图2），下列说法正确的是（）

A、甲、乙的平均数相同 B、乙的成绩更稳定 C、甲、乙的中位数相同 D、甲和乙的众数相同

查看试题解析
11. 以下是代数式 $(\frac{3}{x - 1} - x - 1) \div \frac{x^{2} - 4 x + 4}{x - 1}$ 排乱的化简步骤：
① $= \frac{(2 + x) (2 - x)}{x - 1} \cdot \frac{x - 1}{{(x - 2)}^{2}}$ ；
② $= \frac{2 + x}{2 - x}$ ；
③ $= [\frac{3}{x - 1} - \frac{(x + 1) (x - 1)}{x - 1}] \cdot \frac{x - 1}{{(x - 2)}^{2}}$ ；
④ $= \frac{4 - x^{2}}{x - 1} \cdot \frac{x - 1}{{(x - 2)}^{2}}$ ．
则正确化简步骤的顺序是（）

A、①→③→④→② B、③→①→④→② C、③→④→①→② D、①→④→③→②

查看试题解析
12. 要得知某一池塘两端A，B的距离，发现其无法直接测量，两同学提供了如下间接测量方案．
方案Ⅰ：如图1，先过点B作 $B F ⊥ A B$ ，再在 $B F$ 上取C，D两点，使 $B C = C D$ ，接着过点D作 $B D$ 的垂线 $D E$ ，交 $A C$ 的延长线于点E，则测量 $D E$ 的长即可；
方案Ⅱ：如图2，过点B作 $B D ⊥ A B$ ，再由点D观测，用测角仪在 $A B$ 的延长线上取一点C，使 $∠ B D C = ∠ B D A$ ，则测量 $B C$ 的长即可．
对于方案Ⅰ、Ⅱ，说法正确的是（）

A、只有方案Ⅰ可行 B、只有方案Ⅱ可行 C、方案Ⅰ和Ⅱ都可行 D、方案Ⅰ和Ⅱ都不可行

查看试题解析
13. 我国古代数学著作《九章算术》记载：“今有甲乙二人，持钱不知其数．甲得乙半而钱五十，乙得甲太半而钱亦五十，问甲、乙持钱各几何？”意思是：今有甲、乙二人，不知道其钱包里有多少钱，若把乙钱数的一半给甲，则甲的钱数为 $50$ ，若把甲钱数的三分之二给乙，则乙的钱数也为 $50$ ，问甲、乙各有多少钱？若设甲持钱x，则下列说法错误的是（　　）

A、设乙持钱为y，依题意 ${\begin{array}{l} x + \frac{1}{2} y = 50 \\ y + \frac{2}{3} x = 50 \end{array}$ B、依题意 $(50 - x) + \frac{2}{3} x = 50$ C、乙的钱数为 $25$ D、甲、乙钱数的和为 $62.5$

查看试题解析
14. 如图，将直尺、含 $60 °$ 的直角三角尺和量角器按如图摆放， $60 °$ 角的顶点A在直尺上读数为4，量角器与直尺的接触点B在直尺上的读数为7，量角器与直角三角尺的接触点为点C，则该量角器的直径是（）．

A、3 B、 $3 \sqrt{3}$ C、6 D、 $6 \sqrt{3}$

查看试题解析
15. 如图，点M，N，P，Q，T均为坐标系中2×2的正方形网格的顶点（网格的横线都与x轴平行，纵线都与y轴平行，每个小正方形的边长为1），点N的坐标为 $(2 ， 2)$ ，在曲线l： $y = \frac{k}{x} (x > 0)$ 中的常数k的值从1逐渐增大到9的过程中，关于曲线l依次经过的格点的顺序，下列说法正确的是（）

A、点M→点P→同时经过点N，Q→点T B、点M→点N→同时经过点P，Q→点T C、点M→同时经过点P，Q→点N→点T D、点P→点M→同时经过点N，Q→点T

查看试题解析
16. 题目：“如图，用10个全等的正五边形依次排列可以围成环状．若改为正n边形也能围成环状，除了 $n = 5$ 外，请求出其他所有n的可能的值．”对于其答案，甲答： $n = 6$ ，乙答： $n = 8$ ，则正确的是（）

A、只有甲答的对 B、只有乙答的对 C、甲、乙答案合在一起才完整 D、甲、乙答案合在一起也不完整

查看试题解析

二、填空题

17. 计算： $\sqrt{200} - \sqrt{8} =$ ．

查看试题解析
18. 如图，已知在 $△ A B C$ 中， $A B = 4$ ， $B C = A C = 6$ ，点P是 $A B$ 的中点，过点P的直线与 $A C$ 交于点Q，依据尺规作图痕迹解决下列问题．

(1)、 $P Q$ 与 $B C$ 是否平行？（填“是”或“否”）；

(2)、 $△ A P Q$ 的周长为．

查看试题解析
19. 把1，3，5，7，9…这一组数按如下规律排列放在表格1中，任意选定如图所示方框中的4个数，进行交叉相乘再相减的运算，即 $b c - a d$ ．例如： $3 \times 11 - 1 \times 13 = 20$ ．

(1)、 $9 \times 17 - 7 \times 19 =$ ；

(2)、 $b c - a d =$ ；

(3)、如表2，把1，3，5，7，9…这一组数重新排放在有n列的表格中，则 $b c - a d =$ ．（用含n的式子表示）

查看试题解析

三、解答题

20. 如图，将数轴上 $- 6$ 与6两点间的线段六等分，这五个等分点所对应的数依次为 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ ， $a_{5}$ ．

(1)、 $a_{4} =$ ；

(2)、计算： $a_{1} \cdot a_{4} - a_{3} - a_{2} \div a_{5}$ ．

查看试题解析
21. 如图，公园里有两块边长分别为a，b的正方形区域A、B，其中阴影部分M为雕塑区，面积为m，其他部分种植花草．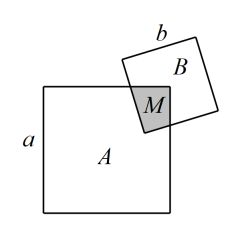

(1)、用含a，b，m的代数式表示种植花草的面积；

(2)、若正方形A的一个顶点恰为正方形B的中心，a比b大20，M的面积是A的 $\frac{1}{9}$ ，求a的值．

查看试题解析
22.

(1)、概念理解
嘉嘉和淇淇学习了随机事件的概率，老师留的作业中有一道判断题：①自然现象中，“太阳从东方升起”是必然事件；②成语“水中捞月”所描述的事件是随机事件；③若抽奖活动的中奖概率为 $\frac{1}{50}$ ，则抽奖50次必中奖1次．

真命题的序号是；

(2)、知识应用
嘉嘉和淇淇做化学实验，紫色石蕊试剂是一种常用的酸碱指示剂，通常情况下石蕊试剂遇酸溶液变红，遇碱溶液变蓝，遇中性溶液不变色．现有4瓶缺失标签的无色液体：蒸馏水、白醋溶液、食用碱溶液、柠檬水溶液，其中白醋溶液、柠檬水溶液是酸性，食用碱溶液是碱性，蒸馏水是中性，两人各取了4个烧杯，分别倒入这4种不同的无色液体．

①嘉嘉将石蕊试剂滴入任意一个烧杯，呈现蓝色的概率是；

②淇淇随机取了两个烧杯，滴入石蕊试剂，用画树状图法或列表法求一杯变红、一杯变蓝的概率．

查看试题解析
23. 网上购物快捷、简便，受到人们的广泛喜爱．小明家装修要用某种环保装饰材料，两个商家的原价相同．购物节优惠促销，甲店打9折，乙店不超过3件不打折，实际付费金额 $y_{甲}$ （元）， $y_{乙}$ （元）和x（件）（x为非负整数）的关系如图所示，小明家需要这种装饰材料6件，发现两家的付费金额恰好相同．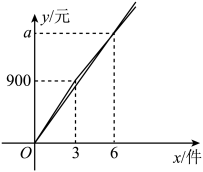

(1)、写出 $y_{甲}$ （元）与x（件）的函数关系式，并求出a的值；

(2)、写出 $y_{乙}$ （元）和x（件）的函数关系式，并写出乙店实际的优惠方案；

(3)、小宇家也需要这种装饰材料，按照上述的优惠方案，已知甲店比乙店付费金额高60元，求小宇家购买的件数．

查看试题解析
24. 图1是一个虎口式夹子的俯视示意图，点O是夹子转轴，点O左边是两段相等的夹弧 $\overset{⌢}{O A}$ 与 $\overset{⌢}{O B}$ （点A与点B重合），右边是长度相等的两部分夹柄， $O E ⊥ C E$ 于点E， $O F ⊥ D F$ 于点F， $O E = O F = 1.4 c m$ ， $C E = D F = 4.8 c m$ ．其中 $O A = O B = 4 c m$ ， $C D = 5 c m$ ．

(1)、求 $O C$ 的长及图1中 $∠ C O D$ 的大小；

(2)、按图2方式用手指按夹柄，夹子两边绕点O转动．当点C，D重合时，两段弧 $\overset{⌢}{O A}$ 与 $\overset{⌢}{O B}$ 恰好在同一圆上，求此时优弧 $\overset{⌢}{A O B}$ 的长．（结果保留π）

查看试题解析
25. 如图，抛物线 $L$ ： $y = a (x - 1) (x - 3)$ 与 $x$ 轴交于 $A$ 、 $B$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C$ 且 $O B = O C$ ，点 $P (m ， n)$ 为抛物线 $L$ 的对称轴右侧图象上的一点（不含顶点）．

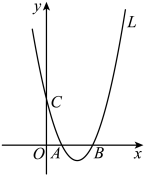(1)、 $a$ 的值为，抛物线的顶点坐标为；

(2)、设抛物线 $L$ 在点 $C$ 和点 $P$ 之间的部分（含点 $C$ 和点 $P$ ）的最高点与最低点的纵坐标之差为 $h$ ，求 $h$ 关于 $m$ 的函数表达式，并写出自变量 $m$ 的取值范围；

(3)、若点 $P (m ， n)$ 的坐标满足 $m + n = 13$ 时，连接 $C P$ ，将直线 $C P$ 与抛物线 $L$ 围成的封闭图形记为 $G$ ．
①求点 $P$ 的坐标；
②直接写出封闭图形 $G$ 的边界上的整点（横、纵坐标都是整数）的个数．

查看试题解析
26. 如图1，等边三角形纸片 $A B C$ 中， $A B = 12$ ，点D在边 $B C$ 上（不与点B、C重合）， $C D = 4$ ，点E在边 $A C$ 上，将 $△ C D E$ 沿 $D E$ 折叠得到 $△ C^{^{'}} D E$ （其中点 $C^{'}$ 是点C的对应点）．

(1)、当点 $C^{'}$ 落在 $A C$ 上时，依题意补全图2，并指出 $C^{'} D$ 与 $A B$ 的位置关系；

(2)、如图3，当点 $C^{'}$ 落到 $∠ A C B$ 的平分线上时，判断四边形 $C D C^{'} E$ 的形状并说明理由；

(3)、当点 $C^{'}$ 到 $A B$ 的距离最小时，求 $C E$ 的长；

(4)、当A， $C^{'}$ ， D三点共线时，直接写出 $∠ A E C^{'}$ 的余弦值．

查看试题解析