深圳市2023年数学六年级下学期期末教学质量检测模拟卷（五）
试卷更新日期：2023-06-21 类型：期末考试
一、单选题
-
1. 一架飞机从某机场向南偏东40°方向飞行了3200千米，返回时飞机要向（ ）。A、南偏东 40°方向飞行 3200 千米 B、西偏北 40°方向飞行 3200 千米 C、南偏西 40°方向飞行 3200 千米 D、北偏西 40°方向飞行 3200 千米2. 某班有学生50人，事假一人，病假一人，则该班的出勤率为（ ）。A、48% B、98% C、96% D、4%3. 用四根木条制作一个长方形框架，双手将它的两个对角慢慢向两边拉动，在这个变化过程中，平行四边形的面积和高（ ）
A、成正比例 B、成反比例 C、不成比例 D、无法判断4. 学校体育活动室有象棋、跳棋共20副，恰好可以供64人同时进行活动，象棋每2人下一副，跳棋每4人下一副。象棋有（ ）副。A、9 B、12 C、15 D、85. 6.1和6.2两班要进行5局乒乓球比赛，前4局的比赛结果如统计表所示。预测第5局的比赛结果，下面说法中正确的是（ ）。比赛局次
1
2
3
4
5
比分（6.1/6.2）
11：8
11：9
11：7
11：9
A、6.1班一定胜 B、6.2班一定胜 C、6.2班不可能胜 D、6.2班有可能胜6. 停车场对小汽车的收费标准是：半小时内（含半小时）免费；半小时以上，每小时收费5元，不足1小时按1小时算。双休日张老师在该停车场付了15元停车费，那么她的停车时间段可能是（ ）。A、8：15-12：00 B、12：30- 14：30 C、11：25-14：45 D、9：55-12：257. 如图所示，长方形被分成甲、乙两个区域，绕轴旋转一周后，甲，乙分别转成的图形的体积相比（ ）。
A、甲大 B、乙大 C、一样大 D、无法确定8. 两杯牛奶，甲杯喝了 ， 乙杯喝了后，两杯剩下的牛奶一样多，原来甲，乙两杯牛奶的比（ ）。A、25：16 B、16：25 C、15：24 D、8：59. 在解决如图4个问题时都运用了（ ）。①用数对确定电影院每一位观众的座位
②求两个数相差多少
③画正比例图像时描点的过程
④锯木头时，锯的段数和次数之间的关系
A、对应思想 B、假设思想 C、逆推策略 D、转化策略10. 一辆汽车从甲地开往乙地，如果车速提高20%，可以比原定的时间提前半小时到达；如果车速降低20%，将会比原定的时间推迟（ ）分钟到达。A、20 B、30 C、45 D、50二、填空题
-
11. +50米表示在起点的东边50米处。如果小军从起点向东走280米后再向西走350米，那么小军这时的位置可以表示为 。12. x和y是两个相关联的量，如果5x=9y，那么x和y成比例；如果y=15÷x，那么x和y成比例。13. 如图所示，把底面半径2厘米、高10厘米的圆柱切成若干等分，拼成一个近似的长方体。这个长方体的底面积是平方厘米，表面积是平方厘米，体积是立方厘米。表面积增加平方厘米
14. 六年级一班有男生20人，女生25人参加了体育活动，男生人数是女生人数的%，男生人数比女生人数少%。15. 把线段比例尺
改写成数值比例尺是 ， 在这幅地图上量得A、B两地之间的距离为3.2cm，A、B两地之间的实际距离是km。 16. 一套运动装打八折销售，比原价便宜了 %，如果这套运动服现在售价200元，则原价是 元。17. 出租车在一定里程内按起步价收费，超出规定里程部分的收费与超出的里程成正比例关系。某出租车公司规定起步里程为3千米，小华乘坐6千米，付费17.5元；小东乘坐14千米，付费37.5元。该出租车公司的起步价是元。18. 甲、乙、丙、丁、戊五位同学参加一次节日活动，很幸运的是，他们都得到了一件精美的礼物，事情是这样的：墙上挂着两串礼物（如图），每次只能从其中一串的最下端取一件，直到礼物取完为止．甲第一个取得礼物，然后，乙、丙、丁、戊依次取得第 件到第 件礼物，当然取法各种各样，那么共有种不同的取法．事后他们打开这些礼物仔细比较，发现礼物 最精美，那么取得礼物 可能性最大的是 ， 可能性最小的是
19. 把一个长14分米、宽12分米、高10分米的长方体木块削成一个最大的圆柱，这个圆柱的体积是立方分米，削去部分的体积是立方分米。20. 如图，4个相同的直角三角形围成了一个正方形，已知a：b=1：2，阴影部分的面积占大正方形面积的 。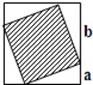
21. 园林绿化队要栽一批树苗，第一天栽了总数的二成五，第二天栽了210棵，这时剩下的与已栽的棵数比是3：2。这批树苗一共有棵。22. 运动员在一个长400米的环形跑道上赛跑，每条跑道宽1.25米，如果要跑400米，每一道的起跑线要比前一道提前米；如果要跑200米，每一道的起跑线要比前一道提前米。三、作图题
-
23. 学校正西方向500米是少年宫，少年宫正北方向300米是动物园，动物园东偏北30度距离400米处是医院。先确定比例尺，再画出上述地点的平面图。
(1)、你选用恰当的比例尺是。(2)、在下边画出上述地点的平面图。24. 在如图的方格图中作图。（每个方格面积表示1平方厘米）
(1)、以虚线为对称轴，画出图形①的另一半，使它成为轴对称图形；(2)、图②中，在B点的北偏西45°方向有一点C，并且和A、B点组成一个面积6cm2的三角形，请确定C点，并画出这个三角形；(3)、将三角形③绕点D顺时针旋转90°，标上④；(4)、在适当的空位上，画出将三角形③按2：1放大后的图形，标上⑤。四、计算题
-
25. 直接写得数。
①1.2÷2.4＝ ② ③9.34＋6.6＝ ④ 0.24×500＝
⑤ ⑥7÷＝ ⑦×2÷×2＝ ⑧
26. 计算下面各题，能简算的要简算(1)、3×15-1.25×15(2)、17+3+2+6.1(3)、 ÷[（+）×](4)、（15-14×）×27. 解方程(1)、 x=4(2)、 x+0.2x=0.16(3)、7（x－1.2）=9.1(4)、 ∶ =28.如图的直角三角形中的空白部分是正方形，正方形的一个顶点将这个直角三角形的斜边分成二部分，求阴影部分的面积．（单位：厘米）
五、解答题
-
29. 受疫情的影响，某商场为了回笼资金，所有商品打七八折出售，已知该商场内一台冰箱打折后的价格比原价便宜了176元，这台冰箱打折后的价格是多少元？30. 某车间为了能高质量准时完成一批齿轮订单，对车间工人提前进行了加工齿轮效率的测试，经过统计测算，平均每个工人加工齿轮效率情况如图：
(1)、根据图象判断，加工齿轮的个数和天数成比例．(2)、加工小齿轮的效率比大齿轮高百分之几？(3)、已知这个车间有工人85人，1个大齿轮和3个小齿轮配为一套，为了使大小齿轮能成套出厂，如果你是车间主任，怎样安排这85名工人最合理？31. 在一个直径是2dm的圆柱形容器中，放入一个底面半径是3cm的圆锥形铁块，全部漫没在水中，这时水面上升0.3cm。圆锥形铁块的高是多少厘米？
