河北省石家庄市九地市2023年中考三模数学试题
试卷更新日期:2023-06-21 类型:中考模拟
一、单选题
-
1. 计算 , 则?=( )A、1 B、5 C、6 D、92. 在中,是的中线.看到图形,甲、乙、丙、丁四名同学给出四个不同的结论,其中正确的是( )
甲:
乙:
丙:
丁:
 A、甲 B、乙 C、丙 D、丁3. 计算的结果是( )A、0 B、 C、6 D、94. 若 , 则的值为( )A、 B、 C、 D、5. 芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一.它作为食品和药物,得到广泛的使用.经测算,一粒芝麻的质量约为 kg,将100粒芝麻的质量用科学记数法表示约为( )A、 kg B、 kg C、 kg D、 kg6. 如图是由若干个棱长为1的小正方体搭成的一个几何体的三视图,则这个几何体的体积是( )
A、甲 B、乙 C、丙 D、丁3. 计算的结果是( )A、0 B、 C、6 D、94. 若 , 则的值为( )A、 B、 C、 D、5. 芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一.它作为食品和药物,得到广泛的使用.经测算,一粒芝麻的质量约为 kg,将100粒芝麻的质量用科学记数法表示约为( )A、 kg B、 kg C、 kg D、 kg6. 如图是由若干个棱长为1的小正方体搭成的一个几何体的三视图,则这个几何体的体积是( ) A、4 B、5 C、6 D、77. 如图,正六边形和正五边形的边重合,的延长线与交于点 , 则的度数是( )
A、4 B、5 C、6 D、77. 如图,正六边形和正五边形的边重合,的延长线与交于点 , 则的度数是( )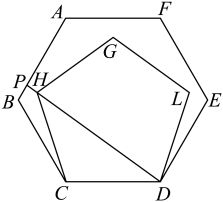 A、 B、 C、 D、8. 若为正整数,则下列运算结果不是负数( )A、 B、 C、 D、9. 如图,证明矩形的对角线相等.已知:四边形 是矩形.求证: .以下是排乱的证明过程:①∴ , ;②∵ ;③∵四边形 是矩形;④∴ ;⑤∴ .
A、 B、 C、 D、8. 若为正整数,则下列运算结果不是负数( )A、 B、 C、 D、9. 如图,证明矩形的对角线相等.已知:四边形 是矩形.求证: .以下是排乱的证明过程:①∴ , ;②∵ ;③∵四边形 是矩形;④∴ ;⑤∴ .
甲的证明顺序是:③①②⑤④
乙的证明顺序是:②③①⑤④
则下列说法正确的是( )
A、甲和乙都对 B、甲和乙都不对 C、甲对乙不对 D、乙对甲不对10. 张华学习了“数轴上的点与实数是一一对应的关系”后,课下便尝试在数轴上找一个表示无理数的点.首先画一条数轴,原点为 , 点表示的数是2,然后过点作 , 使 , 连接 , 以为圆心,长为半径作弧,交数轴负半轴于点 , 则点所表示的数介于( ) A、和之间 B、和之间 C、和之间 D、和之间11. 一大门栏杆的平面示意图如图所示,垂直地面于点 , 平行于地面 , 若 , 则的度数是( )
A、和之间 B、和之间 C、和之间 D、和之间11. 一大门栏杆的平面示意图如图所示,垂直地面于点 , 平行于地面 , 若 , 则的度数是( ) A、110° B、120° C、130° D、135°12. 某校举办的知识竞赛,共道题,规定答对一道题加x分,答错一道题(不答按错)扣分,小明答错了2道题,他得到的分数是( )A、 B、 C、 D、13. 我市某一周内每天的最高气温如下表所示,则这组数据的中位数和众数分别是( )
A、110° B、120° C、130° D、135°12. 某校举办的知识竞赛,共道题,规定答对一道题加x分,答错一道题(不答按错)扣分,小明答错了2道题,他得到的分数是( )A、 B、 C、 D、13. 我市某一周内每天的最高气温如下表所示,则这组数据的中位数和众数分别是( )最高气温()
25
26
27
30
天数
1
1
2
3
A、26.5和28 B、27和30 C、1.5和3 D、2和314. 红星电池厂2022年1~5月份的电池产量如图所示.设从2月份到4月份,该厂电池产量的平均月增长率为x,根据题意可得方程( ) A、 B、 C、 D、15. 如图,平行于y轴的直线分别交 与 的图象(部分)于点A、B,点C是y轴上的动点,则 的面积为( )
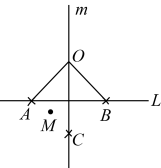
A、 B、 C、 D、15. 如图,平行于y轴的直线分别交 与 的图象(部分)于点A、B,点C是y轴上的动点,则 的面积为( ) A、 B、 C、 D、16. 对于直线L和直线L外的一点O,按下列步骤完成了尺规作图:(1)在直线L的另一侧取点M;(2)以O为圆心,为半径作弧与L交于A,B两点;(3)分别以A,B为圆心,大于为半径作弧,两弧交于点C;(4)过点O和C作直线m.问题:“在直线m上任取一点P(点P不在L上),连接 , , 过点A作直线n与直线垂直,设是 , 直线n与所夹的锐角是 , 求x与y的数量关系.”下面是三个同学的答案,甲: , 乙: , 丙: .
A、 B、 C、 D、16. 对于直线L和直线L外的一点O,按下列步骤完成了尺规作图:(1)在直线L的另一侧取点M;(2)以O为圆心,为半径作弧与L交于A,B两点;(3)分别以A,B为圆心,大于为半径作弧,两弧交于点C;(4)过点O和C作直线m.问题:“在直线m上任取一点P(点P不在L上),连接 , , 过点A作直线n与直线垂直,设是 , 直线n与所夹的锐角是 , 求x与y的数量关系.”下面是三个同学的答案,甲: , 乙: , 丙: .对于三人的答案,下列结论正确的是( )
 A、只有甲的答案正确 B、甲和乙的答案合在一起才正确 C、甲和丙的答案合在一起才正确 D、甲乙丙的答案合在一起才正确
A、只有甲的答案正确 B、甲和乙的答案合在一起才正确 C、甲和丙的答案合在一起才正确 D、甲乙丙的答案合在一起才正确二、填空题
-
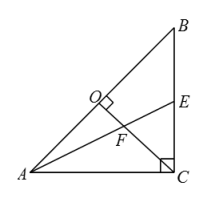
17. 分解因式: =18. 如图,在等腰直角三角形中, , , 于点 , 中线与相交于点 , 则(1)、的值为;(2)、 .
 19. 如图,在中, , , , D是边上一点,线段绕点D顺时针旋转得到 , 连接 , 若F是的中点.
19. 如图,在中, , , , D是边上一点,线段绕点D顺时针旋转得到 , 连接 , 若F是的中点. (1)、与的位置关系是;(2)、当点F在上时,;(3)、的最小值为 .
(1)、与的位置关系是;(2)、当点F在上时,;(3)、的最小值为 .三、解答题
-
20. 下面是5个未化简的有理数: , , , ,(1)、依次写出这五个数的化简结果,并计算它们的平方和;(2)、求这五个数的平均数;(3)、在这5个数中,最大的数是m,最小的数是n.试判别方程根的情况.21. 某乒乓球俱乐部有名男队员和名女队员可参加对外比赛,其中有名男队员和名女队员使用左手打球.现计划用这名队员组成混合双打组合.(以下简称混双组合:就是由一名男队员和一名女队员组成)(1)、可以有多少种不同的混双组合?如果从这些组合中任选个参加比赛,那么选中的组合中正好有一名左手队员和一名右手队员的概率是多少?(2)、实际运作中,通过各种组合之间的比赛,最终确定了个组合,其中有一个组合正好是男号与女号组成的(我们称为“一号组合”).如果这三个组合通过抓阉(jiu)方式决定哪一组由张岩教练指导,直接写出“一号组合”选中张岩教练的概率是多少?22. 发现:当两个不同的正整数同为偶数或奇数时,这两个数之和与这两个数之差的平方差一定能被4整除,且这两个数的积可以表示为两个正整数的平方差.
验证:如,能被4整除,请把3与1的积写成两个正整数的平方差;
探究:设“发现”中两个正整数分别为m,n,请论证“发现”中的结论正确.
23. 如图,直线与坐标轴分别交于点A,C,直线与直线关于y轴对称. (1)、求直线的解析式.(2)、若点在的内部,求m的取值范围.(3)、若过点O的直线L将分成的两部分的面积比为 , 直接写出L的解析式.24. 如图,在中, , 把绕点A顺时针旋转,使落到延长线上的处,得到 , 点B的对应点为D,点C的对应点为E,旋转过程中得到两条弧 , , 与交于点F,连接 .
(1)、求直线的解析式.(2)、若点在的内部,求m的取值范围.(3)、若过点O的直线L将分成的两部分的面积比为 , 直接写出L的解析式.24. 如图,在中, , 把绕点A顺时针旋转,使落到延长线上的处,得到 , 点B的对应点为D,点C的对应点为E,旋转过程中得到两条弧 , , 与交于点F,连接 . (1)、求的度数;(2)、若 , 求阴影部分的面积;(3)、若 , 弧BD与线段只有一个公共点D,直接写出线段的取值范围.25. 如图,排球运动场的场地长18m,球网高度2.24m,球网在场地中央,距离球场左、右边界均为9m.一名球员在场地左侧边界练习发球,排球的飞行路线可以看作是对称轴垂直于水平面的抛物线的一部分.
(1)、求的度数;(2)、若 , 求阴影部分的面积;(3)、若 , 弧BD与线段只有一个公共点D,直接写出线段的取值范围.25. 如图,排球运动场的场地长18m,球网高度2.24m,球网在场地中央,距离球场左、右边界均为9m.一名球员在场地左侧边界练习发球,排球的飞行路线可以看作是对称轴垂直于水平面的抛物线的一部分.
在球运行时,将球与场地左边界的水平距离记为x(米),与地面的高度记为y(米),经多次测试后,得到如下数据:
x(米)
0
1
2
4
6
7
8
y(米)
2
2.15
2.28
2.44
2.5
2.49
2.44
(1)、在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接; (2)、击球点的高度为米,排球飞行过程中可达到的最大高度为米;(3)、求出y与x的函数解析式;(4)、判断排球能否过球网,并说明理由.26. 如图,中, , , , 点P从点C出发,沿的方向运动,点Q从点C出发,沿射线的方向运动,过点Q且与垂直的直线也随之运动.点P的速度是每秒4个单位,点Q的速度是每秒3个单位.点P与点Q同时出发,当点P运动到点B时同时停止.连接 , 设运动时间为t,
(2)、击球点的高度为米,排球飞行过程中可达到的最大高度为米;(3)、求出y与x的函数解析式;(4)、判断排球能否过球网,并说明理由.26. 如图,中, , , , 点P从点C出发,沿的方向运动,点Q从点C出发,沿射线的方向运动,过点Q且与垂直的直线也随之运动.点P的速度是每秒4个单位,点Q的速度是每秒3个单位.点P与点Q同时出发,当点P运动到点B时同时停止.连接 , 设运动时间为t,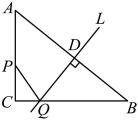 (1)、当点P在上,且不与点C,A重合(即)时,
(1)、当点P在上,且不与点C,A重合(即)时,①求证:;
②当t为何值时与全等.
(2)、直接写出当t为何值时,点P到直线的距离是8.