江西省新余市2023年中考一模数学试题
试卷更新日期:2023-06-21 类型:中考模拟
一、单选题
-
1. 在 , , , 四个实数中,最大的数是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的左视图是()
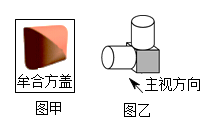 A、
A、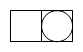
B、
B、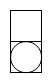
C、
C、
D、
D、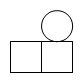
4. 为积极响应国家“双减”政策,鼓励老师积极参加课后服务工作,我市推出“名师公益”大课堂,为学生提供线上线下免费辅导,学生成绩稳中有进,下表是某班小组名同学的测试成绩:
4. 为积极响应国家“双减”政策,鼓励老师积极参加课后服务工作,我市推出“名师公益”大课堂,为学生提供线上线下免费辅导,学生成绩稳中有进,下表是某班小组名同学的测试成绩:学生编号
号
号
号
号
号
号
号
号
成绩单位:分
那么该组同学成绩的中位数和众数分别为( )
A、 , B、 , C、 , D、 ,5. 数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如为实数的数叫做复数,用表示,任何一个复数在平面直角坐标系中都可以用有序数对表示,如:表示为 , 则可表示为( )A、 B、 C、 D、6. 如图,点O为矩形ABCD的对称中心,AD>AB,点E从点B出发(不含点B)沿BC向点C运动,移动到点C停止,延长EO交AD于点F,则四边形BEDF形状的变化依次为( ) A、平行四边形→菱形→正方形→矩形 B、平行四边形→正方形→菱形→矩形 C、平行四边形→菱形→平行四边形→矩形 D、平行四边形→正方形→平行四边形一矩形
A、平行四边形→菱形→正方形→矩形 B、平行四边形→正方形→菱形→矩形 C、平行四边形→菱形→平行四边形→矩形 D、平行四边形→正方形→平行四边形一矩形二、填空题
-
7. 使根式 有意义的x的取值范围是 .8. 十四届全国人大一次会议于年月日时在北京人民大会堂举行,月日时举行闭幕会在百度搜索框输入“十四届全国人大一次会议闭幕”,“百度一下”,综合热度榜显示:“热度”,数据“”用科学记数法表示为 .9. 已知一元二次方程的两个根为 , , 则的值是 .10. 如图,有一个半径为的圆形时钟,其中每个刻度间的弧长均相等,过点和点的位置作一条线段,则钟面中阴影部分的面积为 结果保留 .
 11. 如图所示,是一个运算程序示意图.若第一次输入k的值为125,则第2023次输出的结果是 .
11. 如图所示,是一个运算程序示意图.若第一次输入k的值为125,则第2023次输出的结果是 . 12. 在中, , , , 、分别是边、上的动点将沿直线翻折,使点的对应点恰好落在边上若是等腰三角形,则的长是 .
12. 在中, , , , 、分别是边、上的动点将沿直线翻折,使点的对应点恰好落在边上若是等腰三角形,则的长是 .三、解答题
-
13.(1)、计算: .(2)、如图,在平行四边形中,点 , 分别在边 , 上,且四边形为正方形求证: .
 14. 先化简,再求值: , 其中 .15. 某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.(1)、按约定,“小李同学在该天早餐得到两个油饼”是事件;(可能,必然,不可能)(2)、请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.16. 如图,在边长为的正方形网格中有一段圆弧 , 弧经过格点A、B、C,请仅用无刻度的直尺分别按下列要求画图保留作图痕迹 .
14. 先化简,再求值: , 其中 .15. 某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.(1)、按约定,“小李同学在该天早餐得到两个油饼”是事件;(可能,必然,不可能)(2)、请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.16. 如图,在边长为的正方形网格中有一段圆弧 , 弧经过格点A、B、C,请仅用无刻度的直尺分别按下列要求画图保留作图痕迹 . (1)、在图中,画出弧所在圆的圆心;(2)、在图中,画出弧所在的圆的一条切线,使这条切线经过格点 .17. 为弘扬学生“为人民服务”的精神,月份我区共青团委举办了“弘扬雷锋精神争做美德少年”主题演讲比赛比赛前购买了 , 两种装饰品对比赛场地进行了美化已知用元购买种装饰品与用元购买种装饰品的数量相等,且每个种装饰品的价格比种多元.(1)、A,B两种装饰品的单价各为多少元?(2)、计划购买 , 两种装饰品共个,其中种装饰品的数量不低于种装饰品的 , 且不超过种装饰品数量的 , 请求出共有几种购买方案?18. 习近平总书记在党的二十大报告中指出:“必须坚持科技是第一生产力、人才是第一资源、创新是第一动力”科技兴则民族兴,人才强则国家强为了培养同学们的科技与创新意识,我校科技月组织学生参加“好奇心”科普节的以“好奇点亮未米,理想融入科学”为主题的科技知识答题活动校园小记者调查了本校部分同学,并统计他们的答题得分单位:分情况,然后利用所得数据绘制成如下不完整的统计图表.
(1)、在图中,画出弧所在圆的圆心;(2)、在图中,画出弧所在的圆的一条切线,使这条切线经过格点 .17. 为弘扬学生“为人民服务”的精神,月份我区共青团委举办了“弘扬雷锋精神争做美德少年”主题演讲比赛比赛前购买了 , 两种装饰品对比赛场地进行了美化已知用元购买种装饰品与用元购买种装饰品的数量相等,且每个种装饰品的价格比种多元.(1)、A,B两种装饰品的单价各为多少元?(2)、计划购买 , 两种装饰品共个,其中种装饰品的数量不低于种装饰品的 , 且不超过种装饰品数量的 , 请求出共有几种购买方案?18. 习近平总书记在党的二十大报告中指出:“必须坚持科技是第一生产力、人才是第一资源、创新是第一动力”科技兴则民族兴,人才强则国家强为了培养同学们的科技与创新意识,我校科技月组织学生参加“好奇心”科普节的以“好奇点亮未米,理想融入科学”为主题的科技知识答题活动校园小记者调查了本校部分同学,并统计他们的答题得分单位:分情况,然后利用所得数据绘制成如下不完整的统计图表.答题得分频数分布表
组别
答题得分分
人数
 根据图表,解答下列问题:(1)、校园小记者“调查了本校部分同学”采取的调查方式是: 调查请选填“全面”、“随机抽样”;(2)、这次被调查的同学共有 人, , ;(3)、求扇形统计图中扇形的圆心角的度数;(4)、若该校有名学生,请估计全校有多少学生答题得分不少于分?19. 小李使用握力器如实物图所示锻炼手部肌肉如图,点是弹簧的上端点,调节处的螺旋调节器,弹簧的下端点可在上的一段凹槽内移动,从而调节握力器的握力大小小李开始锻炼时将弹簧的下端点调到点处,此时弹簧的弹力是 , , 经过一段时间的锻炼后,小李想增加锻炼强度,将弹簧下端点调至处,此时弹簧的弹力是 , , 已知点到的距离是 .
根据图表,解答下列问题:(1)、校园小记者“调查了本校部分同学”采取的调查方式是: 调查请选填“全面”、“随机抽样”;(2)、这次被调查的同学共有 人, , ;(3)、求扇形统计图中扇形的圆心角的度数;(4)、若该校有名学生,请估计全校有多少学生答题得分不少于分?19. 小李使用握力器如实物图所示锻炼手部肌肉如图,点是弹簧的上端点,调节处的螺旋调节器,弹簧的下端点可在上的一段凹槽内移动,从而调节握力器的握力大小小李开始锻炼时将弹簧的下端点调到点处,此时弹簧的弹力是 , , 经过一段时间的锻炼后,小李想增加锻炼强度,将弹簧下端点调至处,此时弹簧的弹力是 , , 已知点到的距离是 . (1)、求的长结果保留一位小数(2)、在弹性限度内,弹簧的弹力变化量与弹簧长度的变化量成正比,即其中为弹簧的弹力的变化量,为弹簧的劲度系数,单位为 , 为弹簧长度的变化量求该弹簧的劲度系数 . 参考数据: , ,20. 如图,点、是一次函数与反比例函数图象的交点,点在轴上运动,请结合图象解决下列问题:
(1)、求的长结果保留一位小数(2)、在弹性限度内,弹簧的弹力变化量与弹簧长度的变化量成正比,即其中为弹簧的弹力的变化量,为弹簧的劲度系数,单位为 , 为弹簧长度的变化量求该弹簧的劲度系数 . 参考数据: , ,20. 如图,点、是一次函数与反比例函数图象的交点,点在轴上运动,请结合图象解决下列问题: (1)、求点、的坐标及的面积;(2)、根据图象直接写出当取什么值时,?(3)、点在轴上运动的过程中,
(1)、求点、的坐标及的面积;(2)、根据图象直接写出当取什么值时,?(3)、点在轴上运动的过程中,①直接写出的最小值: .
②的面积是否发生变化,如果变化,请说明理由;如果不变化,请求出的面积.
21. 是的外接圆, , 延长至点. (1)、如图 , 若 , 且B为弧的中点,求证:是的切线;(2)、如图 , 若是的切线,且 , , 求圆的半径及弦的长.22. 在中, , , , 点 , 分别是 , 线段上的点,且满足 , 连接 , 将绕着点逆时针旋转,记旋转角为 .
(1)、如图 , 若 , 且B为弧的中点,求证:是的切线;(2)、如图 , 若是的切线,且 , , 求圆的半径及弦的长.22. 在中, , , , 点 , 分别是 , 线段上的点,且满足 , 连接 , 将绕着点逆时针旋转,记旋转角为 . (1)、①当 , 时 ;
(1)、①当 , 时 ;②当时, .
(2)、如图 , 当时,过点作于点 , 过作于点 , 求出的值;(3)、当时,若为的中点,求在旋转过程中,线段长的最大值和最小值.23. 定义:在平面直角坐标系中,抛物线与轴的交点坐标为 , 那么我们把经过点且平行于轴的直线称为这条抛物线的极限分割线.(1)、 【特例感知】抛物线的极限分割线与这条抛物线的交点坐标为 .
(2)、 【深入探究】经过点和的抛物线与轴交于点 , 它的极限分割线与该抛物线另一个交点为 , 请用含的代数式表示点的坐标.
(3)、 【拓展运用】在(2)的条件下,设抛物线的顶点为 , 直线垂直平分 , 垂足为 , 交该抛物线的对称轴于点 .
①当时,求点的坐标.
②若直线与直线关于极限分割线对称,是否存在使点到直线的距离与点到直线的距离相等的的值?若存在,直接写出的值;若不存在,请说明理由.