山东省潍坊市2023年中考三模数学试题
试卷更新日期:2023-06-21 类型:中考模拟
一、单选题
-
1. 下列计算结果正确的是( )A、 B、 C、 D、2. 星载原子钟是卫星导航系统的“心脏”,对系统定位和授时精度具有决定性作用.“北斗”三号卫星导航系统装载国产高精度星载原子钟,保证“北斗”优于20纳秒的授时精度. 1纳秒秒,那么20纳秒用科学记数法表示应为( )A、秒 B、秒 C、秒 D、秒3. 如图1是由6个相同的小正方块组成的几何体,移动其中一个小正方块,变成图2所示的几何体( )
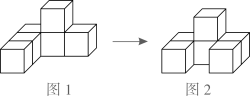 A、主视图改变,俯视图改变 B、主视图不变,俯视图改变 C、主视图不变,俯视图不变 D、主视图改变,俯视图不变4. 把一块等腰直角三角板和一把直尺按如图所示的位置构成,若∠1=25°,则∠2的度数为( )
A、主视图改变,俯视图改变 B、主视图不变,俯视图改变 C、主视图不变,俯视图不变 D、主视图改变,俯视图不变4. 把一块等腰直角三角板和一把直尺按如图所示的位置构成,若∠1=25°,则∠2的度数为( ) A、15° B、20° C、25° D、30°5. 如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流与电阻成反比例函数的图象,该图象经过点.根据图象可知,下列说法正确的是( )
A、15° B、20° C、25° D、30°5. 如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流与电阻成反比例函数的图象,该图象经过点.根据图象可知,下列说法正确的是( ) A、当时, B、I与R的函数关系式是 C、当时, D、当时,I的取值范围是6. 某函数的图象如图所示,当时,在该函数图象上可找到个不同的点 , , ……, , 使得 , 则的取值不可能为( )
A、当时, B、I与R的函数关系式是 C、当时, D、当时,I的取值范围是6. 某函数的图象如图所示,当时,在该函数图象上可找到个不同的点 , , ……, , 使得 , 则的取值不可能为( )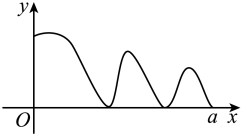 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、多选题
-
7. 实数a在数轴上的对应点的位置如图所示,若实数b满足 , 则b的值可以是( )
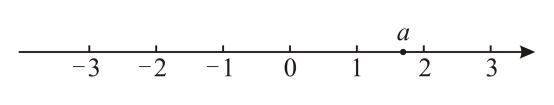 A、2 B、 C、 D、1
A、2 B、 C、 D、1三、单选题
-
8. 疾控中心每学期都对我校学生进行健康体检,小亮将领航班所有学生测量体温的结果制成如下统计图表.下列说法正确的是( )
体温
人数/人
4
8
8
10
m
2
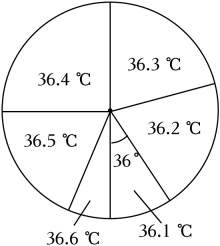 A、这个班有40名学生 B、 C、这些体温的众数是8 D、这些体温的中位数是36.359. 如图,抛物线的对称轴是直线 , 则下列结论正确的是( )
A、这个班有40名学生 B、 C、这些体温的众数是8 D、这些体温的中位数是36.359. 如图,抛物线的对称轴是直线 , 则下列结论正确的是( )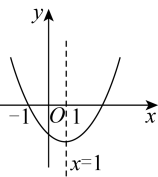 A、 B、 C、 D、
A、 B、 C、 D、四、多选题
-
10. 如图,在正方形纸片中,对角线 , 交于点 , 折叠正方形纸片 , 使落在上,点恰好与上的点重合,展开后,折痕分别交 , 于点 , , 连接 , 下列结论正确的是( ).
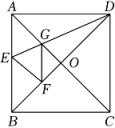 A、 B、 C、 D、四边形是菱形
A、 B、 C、 D、四边形是菱形五、填空题
-
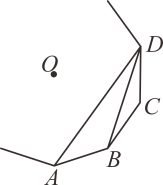
11. 分解因式: .12. 疫情期间居民为了减少外出时间,大家更愿意使用APP在线上买菜,某买菜APP今年一月份新注册用户为200万,三月份新注册用户为338万,则二、三两个月新注册用户每月平均增长率是.13. 如图, 、 、 、 为一个正多边形的顶点, 为正多边形的中心,若 ,则这个正多边形的边数为.
 14. 如图,在中, , 延长至 , 使得 , 点为动点,且 , 连接 , 则的最小值为 .
14. 如图,在中, , 延长至 , 使得 , 点为动点,且 , 连接 , 则的最小值为 .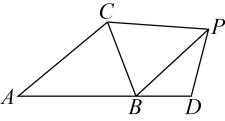
六、解答题
-
15.(1)、计算:;(2)、解不等式组:16. 如图,小明练习册上的一个等腰三角形被墨迹污染了,只有它的底边和还保留着.
 (1)、小明要在练习册上画出原来的等腰 , 用到的基本作图可以是 (填写正确答案的序号);
(1)、小明要在练习册上画出原来的等腰 , 用到的基本作图可以是 (填写正确答案的序号);①作一条线段等于已知线段;②作一个角等于已知角;③作已知角的平分线;④作已知线段的垂直平分线;⑤过一点作已知直线的垂线;
(2)、为边上的中线,若的一个外角为 , 求的度数.17. 为了解市民对全市创卫工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.请结合图中信息,解决下列问题: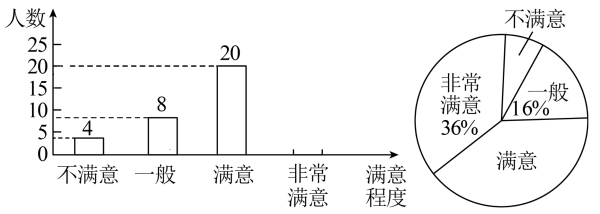 (1)、求此次调查中接受调查的人数,并补全条形统计图.(2)、若本市人口300万人,估算该市对市创卫工作表示满意和非常满意的人数.(3)、兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自同区的概率.18. 如图,光从空气斜射入水中,入射光线射到水池的水面B点后折射光线射到池底点D处,入射角 , 折射角;入射光线射到水池的水面C点后折射光线射到池底点E处,入射角 , 折射角 . , 、为法线.入射光线、和折射光线、及法线、都在同一平面内,点A到直线的距离为6米.
(1)、求此次调查中接受调查的人数,并补全条形统计图.(2)、若本市人口300万人,估算该市对市创卫工作表示满意和非常满意的人数.(3)、兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自同区的概率.18. 如图,光从空气斜射入水中,入射光线射到水池的水面B点后折射光线射到池底点D处,入射角 , 折射角;入射光线射到水池的水面C点后折射光线射到池底点E处,入射角 , 折射角 . , 、为法线.入射光线、和折射光线、及法线、都在同一平面内,点A到直线的距离为6米.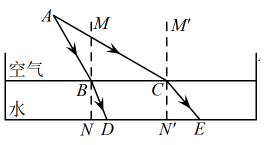 (1)、求的长;(结果保留根号)(2)、如果米,求水池的深.(参考数据:取1.41,取1.73,取0.37,取0.93,取0.4,取0.65,取0.76,取0.85)19. 在初中阶段的函数学习中,我们经历了“确定函数的表达式,利用函数图象研究其性质,运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.学习了一次函数之后,现在来解决下面的问题:
(1)、求的长;(结果保留根号)(2)、如果米,求水池的深.(参考数据:取1.41,取1.73,取0.37,取0.93,取0.4,取0.65,取0.76,取0.85)19. 在初中阶段的函数学习中,我们经历了“确定函数的表达式,利用函数图象研究其性质,运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.学习了一次函数之后,现在来解决下面的问题:在中,下表是y与x的几组对应值.
…
0
1
2
3
…
…
7
3
1
1
3
…
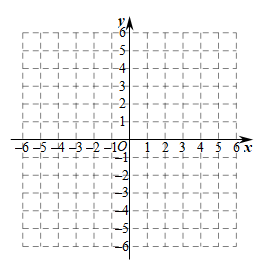 (1)、 , ;(2)、平面直角坐标系中,画出函数的图象;(3)、根据图象,判断下列关于该函数性质的说法是否正确,正确的打√,错误的打×.
(1)、 , ;(2)、平面直角坐标系中,画出函数的图象;(3)、根据图象,判断下列关于该函数性质的说法是否正确,正确的打√,错误的打×.①该函数图象是轴对称图形,对称轴为直线 . ( )
②当时,y随x的增大而增大,当时,y随x的增大而减小.( )
③该函数在自变量的取值范围内有最小值,当时有最小值 . ( )
(4)、若方程组有且只有一个公共解,则t的取值范围是 .20. 振华公司对其办公楼大厅一块6×6米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修,中心区域是正方形 , 用材料乙装修).两种材料的成本如下:材料
甲
乙
单价(元/米)
800
600
设矩形的较短边的长为x米,装修材料的总费用为y元.
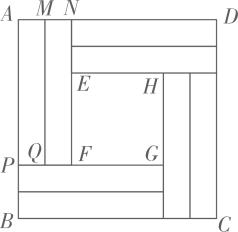 (1)、求y与x之间的关系式;(2)、当中心区域的边长EF不小于2米时,预备材料的购买资金28000元够用吗?请说明理由.21. 【定义】从一个已知图形的外一点引两条射线分别经过该已知图形的两点,则这两条射线所成的最大角称为该点对已知图形的视角,如图①,是点P对线段的视角.
(1)、求y与x之间的关系式;(2)、当中心区域的边长EF不小于2米时,预备材料的购买资金28000元够用吗?请说明理由.21. 【定义】从一个已知图形的外一点引两条射线分别经过该已知图形的两点,则这两条射线所成的最大角称为该点对已知图形的视角,如图①,是点P对线段的视角.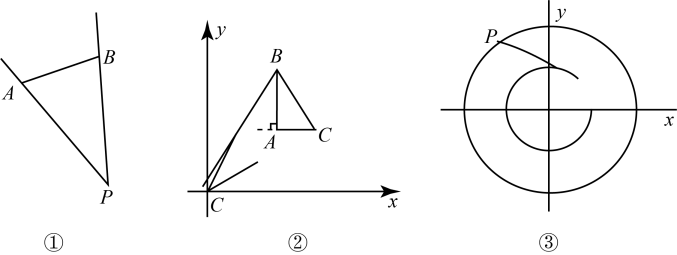 (1)、【应用】
(1)、【应用】
如图②,在直角坐标系中,已知点 , , , 则原点O对三角形的视角为;(2)、如图③,在直角坐标系中,以原点O,半径为2画圆 , 以原点O,半径为4画圆 , 证明:圆上任意一点P对圆的视角是定值;(3)、【拓展应用】
很多摄影爱好者喜欢在天桥上对城市的标志性建筑拍照,如图④.现在有一条笔直的天桥,标志性建筑外延呈正方形,摄影师想在天桥上找到对建筑视角为的位置拍摄.现以建筑的中心为原点建立如图⑤的坐标系,此时天桥所在的直线的表达式为 , 正方形建筑的边长为4,请直接写出直线上满足条件的位置坐标.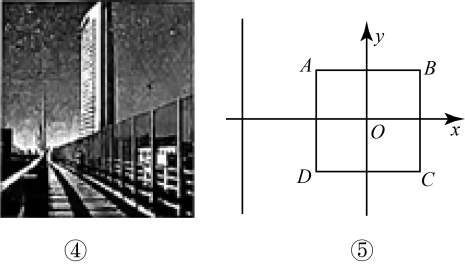 22. 如图1,将一个等腰直角三角尺的顶点C放置在直线l上, , , 过点A作于点D,过点B作于点E.
22. 如图1,将一个等腰直角三角尺的顶点C放置在直线l上, , , 过点A作于点D,过点B作于点E.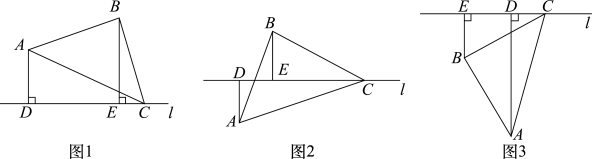 (1)、 观察发现:
(1)、 观察发现:如图1,当A,B两点均在直线l的上方时
①猜测线段与的数量关系并说理由;
②直接写出线段与的数量关系;
(2)、 操作证明:将等腰直角三角尺绕着点C逆时针旋转至图2位置时,线段与又有怎样的数量关系,请写出你的猜想,并写出证明过程;
(3)、 拓广探索:将等腰直角三角尺绕着点C继续旋转至图3位置时,与交于点H,若 , , 请直接写出的长度.
-
-