江西省吉安市2023年中考三模数学试题

试卷更新日期：2023-06-21 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列为负数的是（　　）

A、 $| - 3 |$ B、 $- {(- 1)}^{2024}$ C、 ${(- 2)}^{0}$ D、 ${(- 2)}^{- 2}$

查看试题解析
2. 2022北京冬奥会开幕式的地屏为观众呈现了一场精彩的视觉盛宴．它是由46504个面积为 $2500 c m^{2}$ 的单元箱体组成的，是目前世界上最大规模的 $L E D$ 舞台，能够呈现裸眼3D效果，则该地屏的总面积用科学记数法可表示为（　　）

A、 $4.6504 \times 1 0^{4}$ cm² B、 $1.1626 \times 1 0^{8}$ cm² C、 $1.1626 \times 1 0^{9}$ cm² D、 $2.5 \times 1 0^{3}$ cm²

查看试题解析
3. 从图1的正方体上截去一个三棱锥后，得到如图2所示的几何体，则这个几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 求 $| \frac{1}{2} x - 1 | + | \frac{1}{3} x - 2 | + | \frac{1}{4} x - 3 |$ 的最小值（　　）

A、12 B、6 C、 $\frac{7}{2}$ D、3

查看试题解析
5. 一款简易电子秤的工作原理：一个装有踏板（踏板质量忽略不计）的可变电阻 $R_{2}$ ， $R_{2}$ 与踏板人的质量m之间的函数关系式为 $R_{2} = - 2 m + 240 (0 \leq m \leq 120)$ ，其图象如图1所示；图2的电路中，电源电压恒为12伏，定值电阻 $R_{1}$ 的阻值为60欧，接通开关，人站上踏板，电流表显示的读数为I安，该读数可以换算为人的质量m，电流表量程为0~0.2安（温馨提示：导体两端的电压U，导体的电阻R，通过导体的电流I，满足关系式 $I = \frac{U}{R}$ ），则下面结论错误的为（）

A、用含I的代数式表示 $m$ 为 $m = 150 - \frac{6}{I}$ B、电子体重秤可称的最大质量为120千克 C、当 $m = 115$ 时，若电源电压U为12（伏），则定值电阻 $R_{1}$ 最小为70（欧） D、当 $m = 115$ 时，若定值电阻 $R_{1}$ 为40（欧），则电源电压U最大为10（伏）

查看试题解析
6. 用10根小棒组成如图1所示的图案，请平移3根小棒变成如图2所示的图案，平移的方式有（　　）

A、1种 B、2种 C、3种 D、4种

查看试题解析

二、填空题

7. 分解因式： $x^{4} + 2 x^{3} + 3 x^{2} + 2 x + 1$ = ．

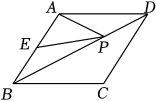
查看试题解析
8. 一组2，2x，y，12中，唯一的众数是12，平均数是10，这数据的中位数是．

查看试题解析
9. 如图，在菱形 $A B C D$ 中， $∠ A B C = 60 °$ ，点 $E$ 为边 $A B$ 的中点，点 $P$ 在对角线 $B D$ 上运动，且 $P E + P A = 12$ ，则 $A B$ 长的最大值为．

查看试题解析
10. 如果方程 $(x - 1) (x^{2} - 2 x + \frac{k}{4}) = 0$ 的三根可以作为一个三角形的三边之长，那么实数 $k$ 的取值范围是．

查看试题解析
11. 对于坐标平面内的点，先将该点向右平移1个单位，再向上平移2个单位，这种点的运动称为点的斜平移，如点 $P (2 ， 3)$ 经1次斜平移后的点的坐标为 $(3 ， 5)$ ．已知点 $A$ 的坐标为 $(1 ， 0)$ ．如图，点 $M$ 是直线 $l$ 上的一点，点 $A$ 关于点 $M$ 的对称点为点 $B$ ，点 $B$ 关于直线 $l$ 的对称点为点 $C$ ．若点 $B$ 由点 $A$ 经 $n$ 次斜平移后得到，且点 $C$ 的坐标为 $(7 ， 6)$ ，则点 $B$ 的坐标为．

查看试题解析
12. 如图，在 $R t Δ A B C$ 中， $∠ B A C = 60 °$ ， $B C = \sqrt{3}$ ， $D$ 是 $B C$ 边上一动点，过点 $D$ 作 $D E ⊥ A B$ 于点 $E$ ．连接 $A D$ ， $Δ A D E^{'}$ 与 $Δ A D E$ 关于 $A D$ 所在的直线对称，且 $A E^{'}$ 所在的直线与直线 $B C$ 相交于点 $F$ ，直线 $B E^{'}$ 与直线 $A C$ 相交于点 $H$ ．若点 $E^{'}$ 到 $R t Δ A B C$ 的斜边和一条直角边的距离恰好相等，则 $C H$ 的长为．

查看试题解析

三、解答题

13.

(1)、计算： $| - \sqrt{2} | - (- 1)^{2024} - (- 2)^{- 1} + (\frac{π}{\sqrt{2} - 1})^{0} - 2 s i n 45 °$ ；

(2)、数学实践活动中，将一张平行四边形纸片 $A B C D$ 进行折叠（如图所示），折痕为 $A E$ ，点 $E$ 在 $B C$ 边上，点 $B$ 落在点 $F$ 处．若点 $E$ 是 $B C$ 边的中点，且 $A E = A B = 10$ ， $B C = 14$ ，求 $C F$ 的长．

查看试题解析
14. 先化简 $(\frac{a}{a^{2} - 3 a} - \frac{2 a}{a^{2} - 9}) \div \frac{a - 2}{a^{2} + 6 a + 9}$ ，然后从不等式组 ${\begin{array}{l} 2 a + 3 > a - 1 ， \\ a + 8 ⩾ 4 a - 1 \end{array}$ 的解集中选取一个你认为合适的整数作为a的值代入求值．

查看试题解析
15. 2022年12月18日卡塔尔世界杯闭幕，以下是吉祥物 $l a^{'} e e b$ ，足球AL RIHLA和大力神杯．现有形状大小完全相同的3张卡片，背面分别印有上述图案，用编号A，B，C来表示．现将这3张卡片背面朝上，洗匀放好．

(1)、从中任意抽取一个张卡片，恰好是“大力神杯”的概率为；

(2)、先从3张卡片中随机抽取一张，记下图案后放回洗匀，再从中随机抽取一张卡片，请用“画树状图”或“列表”的方法求出抽得的2张卡片图案不相同的概率．

查看试题解析
16. 如图，在单位长度为1的 $2 \times 4$ 的网格中，优弧 $A E F$ 上的三点A、E、F均为格点，连接格点 $P D 、 P E ， P E$ 交优弧 $A E F$ 于点C．请完成如下解答任务：

(1)、使用无刻度直尺作 $A E F$ 所在圆的圆心O（简要说明理由）；

(2)、直接写出 $∠ P D B + ∠ P E B$ 的度数为；

(3)、在第（1）、（2）的基础上，求 $A G$ 的长．

查看试题解析
17. 如图，在四边形 $A B C D$ 中， $A B ∥ D C$ ，对角线 $A C$ ， $B D$ 交于点 $O$ ， $A O = C O$ ，且 $A C$ 平分 $∠ B A D$ ，过点 $C$ 作 $C E ⊥ A B$ 交 $A B$ 的延长线于点 $E$ .

(1)、求证：四边形 $A B C D$ 是菱形；

(2)、若 $A B = \sqrt{5}$ ， $B D = 2$ ，求 $△ A C E$ 的面积.

查看试题解析

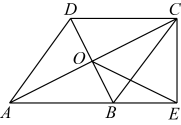18. 在全国中小学生安全教育日来临之际，某校为了加强学生对于各类安全常识了解程度，在八、九年级学生（各有 500 人）中，开展了安全常识知识竞答活动，满分100分．然后随机各抽取20名同学的成绩进行了收集、整理与分析，过程如下：

【收集数据】

八年级：

61	80	86	83	95	100	90	95	75	92
75	80	100	87	97	78	68	84	99	95

九年级：

82	83	91	100	96	79	90	63	90	91
80	86	97	90	85	81	69	90	79	98

【整理数据】

成绩x（单位：分）	61≤x≤70	71≤x≤80	81≤x≤90	91≤x≤100
八年级	2	5	5	8
九年级	2	a	9	6

【分析数据】

年级	统计量
年级	平均数	众数	中位数	方差
八年级	86	95	b	115.9
九年级	86	90	88	83.9

请根据以上信息，回答以下问题：

(1)、填空∶a=；b= ．

(2)、若九年级准备对知识竞答达到95 分的同学给予奖励，那么大约有名学生将会获得奖励．

(3)、结合以上数据，你认为哪个年级的总体成绩更好，请说出你的理由．

查看试题解析

19. 设函数 $y_{1} = \frac{k_{1}}{x}$ ，函数 $y_{2} = k_{2} x + b$ （ $k_{1}$ ， $k_{2}$ ， b是常数， $k_{1} \neq 0$ ， $k_{2} \neq 0$ ）．

(1)、如图①，若函数 $y_{1}$ 和函数 $y_{2}$ 的图象交于点 $A (1 ， m)$ ， $B (3 ， 1)$ ，
①求 $y_{1}$ ， $y_{2}$ 的函数表达式；

②直接写出当 $y_{1} > y_{2}$ 时，自变量x的取值范围；

(2)、如图②，若点 $C (1 ， n)$ 在函数 $y_{1}$ 的图象上，点C先向下平移2个单位长度，再向右平移1个单位长度，得点D，点D恰好落在函数 $y_{1}$ 的图象上，点P在y轴上，求 $△ P C D$ 周长的最小值．

查看试题解析
20. 小明家住在某小区一楼，购房时开发商赠送了一个露天活动场所，现小明在活动场所正对的墙上安装了一个遮阳棚 $B C$ ，经测量，安装遮阳棚的那面墙 $A B$ 高 $3 m$ ，安装的遮阳棚展开后可以使正午时刻房前能有 $2 m$ 宽的阴影处 $(A D)$ 以供纳凉．已知正午时刻太阳光与水平地面的夹角为 $63.4 °$ ，安装好的遮阳篷 $B C$ 与水平面的夹角为 $10 °$ ，如下右图为侧面示意图．

（参考数据： $s i n 10 ° \approx 0.17$ ， $c o s 10 ° \approx 0.98$ ， $t a n 10 ° \approx 0.18$ ， $s i n 63.4 ° \approx 0.89$ ， $c o s 63.4 ° \approx 0.45$ ， $t a n 63.4 ° \approx 2.00$ ）

(1)、据研究，当一个人从遮阳棚进出时，如果遮阳棚外端（即图中点C）到地面的距离小于 $2.3 m$ 时，则人进出时总会觉得没有安全感，就会不自觉的低下头或者用手护着头，请你通过计算，判断此遮阳棚是否使得人进出时具有安全感？

(2)、请计算此遮阳棚延展后的长度（即 $B C$ 的长度）．（结果精确到 $0.1 m$ ）

查看试题解析
21. 如图， $P A$ 是圆O的切线，切点为A， $A C$ 是圆O的直径，连接 $O P$ 交圆O于E．过A点作 $A B ⊥ P O$ 于点D，交圆O于B，连接 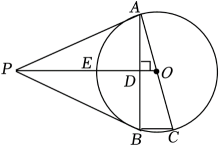$B C ， P B$ ．

(1)、求证： $P O ∥ B C$ ；

(2)、求证： $P B$ 是圆O的切线；

(3)、若 $c o s ∠ P A B = \frac{\sqrt{10}}{10} ， B C = 1$ ，求 $P O$ 的长．

查看试题解析
22. 如图①，灌溉车沿着平行于绿化带底部边线l的方向行驶，为绿化带浇水．喷水口H离地竖直高度 $O H = 1.5$ 米．如图②，可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象；把绿化带横截面抽象为矩形 $D E F G$ ，其水平宽度 $D E = 2$ 米，竖直高度 $E F = 1$ 米．下边缘抛物线可以看作由上边缘抛物线向左平移得到，上边缘抛物线最高点A离喷水口的水平距离为2米，高出喷水口 $0.5$ 米，灌溉车到l的距离 $O D$ 为d米．

(1)、求上边缘抛物线的函数表达式，并求喷出水的最大射程 $O C$ ；

(2)、求下边缘抛物线与x轴的正半轴交点B的坐标；

(3)、要使灌溉车行驶时喷出的水能浇灌到整个绿化带（即矩形 $D E F C$ 位于上边缘抛物线和下边缘抛物线所夹区域内），求d的取值范围．

查看试题解析
23. 问题提出
在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，点D是 $A B$ 的中点，连接 $C D$ ， $△ A D C$ 绕着点A逆时针旋转得到 $△ A M N$ ，连接 $C M ， B N$ ，点G，H分别为 $C M ， B N$ 的中点，连接 $G H$ ，试探究 $G H$ 与 $M C$ 之间有怎样的数量关系和位置关系？

问题解决

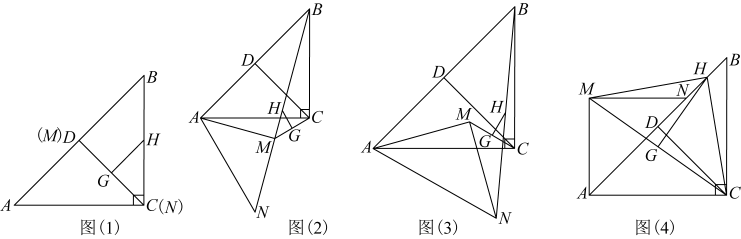(1)、先将问题特殊化：如图（1），当旋转角为0°，即处于起始位置时， $G H$ 与 $M C$ 的数量关系是，位置关系是．

(2)、继续研究特殊情形：如图（2），当点M在线段 $B N$ 上时，（1）中的结论是否成立？若成立，证明结论；若不成立，请说明理由．

(3)、由此归纳一般结论：如图（3），在旋转过程中， $G H$ 与 $M C$ 之间的数量关系是，位置关系是．

(4)、拓展应用
如图（4），当将 $△ A D C$ 绕点A逆时针旋转 $45 °$ 时，连接 $H C ， H M ， △ M C H$ 的面积为 $\frac{3}{8}$ ，应用上述探究的结论，求 $A C$ 的长．

查看试题解析