新疆克拉玛依白碱滩区2023年中考二模数学试题

试卷更新日期：2023-06-21 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 2$ 的绝对值是（　　）

A、2 B、 $- 2$ C、 $\pm 2$ D、 $- \frac{1}{2}$

查看试题解析
2. 如图是某几何体的三视图，该几何体是（）

A、三棱柱 B、长方体 C、圆锥 D、球

查看试题解析
3. 下列计算正确的是（）

A、 $a b^{2} \div a b = b$ B、 $(a - b)^{2} = a^{2} - b^{2}$ C、 $2 m^{4} + 3 m^{4} = 5 m^{8}$ D、 $(- 2 a)^{3} = - 6 a^{3}$

查看试题解析
4. 如图，直线 $a ∥ b$ ，一个三角板的直角顶点在直线a上，两直角边均与直线b相交， $∠ 1 = 40 °$ ，则 $∠ 2 =$ （）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $65 °$

查看试题解析
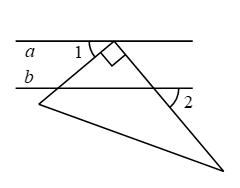5. 已知关于x的方程 $x^{2} + m x + 3 = 0$ 的一个根为 $x = 1$ ，则实数m的值为（　　）

A、4 B、 $- 4$ C、3 D、 $- 3$

查看试题解析
6. 若点 $A (a ， - 1)$ 与点 $B (2 ， b)$ 关于y轴对称，则 $a - b$ 的值是（）

A、 $- 1$ B、 $- 3$ C、1 D、2

查看试题解析
7. 关于二次函数 $y = {(x - 1)}^{2} + 5$ ，下列说法正确的是（）

A、函数图象的开口向下 B、函数图象的顶点坐标是 $(- 1 ， 5)$ C、该函数有最大值，是大值是5 D、当 $x > 1$ 时，y随x的增大而增大

查看试题解析
8. 某地开展建设绿色家园活动，活动期间，计划每天种植相同数量的树木，该活动开始后、实际每天比原计划每天多植树50棵，实际植树400棵所需时间与原计划植树300棵所需时间相同．设实际每天植树x棵．则下列方程正确的是（）

A、 $\frac{400}{x - 50} = \frac{300}{x}$ B、 $\frac{300}{x - 50} = \frac{400}{x}$ C、 $\frac{400}{x + 50} = \frac{300}{x}$ D、 $\frac{300}{x + 50} = \frac{400}{x}$

查看试题解析
9. 我们知道，一元二次方程x²=﹣1没有实数根，即不存在一个实数的平方等于﹣1．若我们规定一个新数“i”，使其满足i²=﹣1（即方程x²=﹣1有一个根为i）．并且进一步规定：一切实数可以与新数进行四则运算，且原有运算律和运算法则仍然成立，于是有i¹=i，i²=﹣1，i³=i²•i=（﹣1）•i=﹣i，i⁴=（i²）²=（﹣1）²=1，从而对于任意正整数n，我们可以得到i⁴ⁿ⁺¹=i⁴ⁿ•i=（i⁴）ⁿ•i=i，同理可得i⁴ⁿ⁺²=﹣1，i⁴ⁿ⁺³=﹣i，i⁴ⁿ=1．那么i+i²+i³+i⁴+…+i²⁰¹²+i²⁰¹³的值为【】

A、0 B、1 C、﹣1 D、i

查看试题解析

二、填空题

10. 二次根式 $\sqrt{x + 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
11. 在平面直角坐标系 $x O y$ 中，若点 $A (2 ， y_{1}) ， B (5 ， y_{2})$ 在反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上，则 $y_{1}$ $y_{2}$ （填“>”“=”或“<”）

查看试题解析
12. 将标有“中”“华”“崛”“起”的四个小球装在一个不透明的口袋中（每个小球上仅标一个汉字），这些小球除所标汉字不同外，其余均相同．从中随机摸出两个球，则摸到的球上的汉字可以组成“中华”的概率是．

查看试题解析
13. 将一个底面直径为6cm，母线长为10cm的圆锥沿一条母线剪开，所得的侧面展开图的面积为cm² ．

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 4$ ， $t a n B = \frac{4}{3}$ ，点B为圆心， $B C$ 长为半径画弧，与 $A B$ 交于点D，再分别以A、D为圆心，大于 $\frac{1}{2} A D$ 的长为半径画弧，两弧交于点M、N，作直线 $M N$ ，分别交 $A C$ 、 $A B$ 于点E、F，则 $B C$ 的长度为， $A E$ 的长度为．

查看试题解析
15. 如图是抛物线 $y_{1} = a x^{2} + b x + c (a \neq 0)$ 图象的一部分，抛物线的顶点坐标为 $A (1 ， - 3)$ ，与x轴的一个交点为 $B (4 ， 0)$ ，点A和点B均在直线 $y_{2} = m x + n (m \neq 0)$ 上．① $2 a + b = 0$ ；② $a b c < 0$ ；③抛物线与x轴的另一个交点为 $(- 4 ， 0)$ ；④方程 $a x^{2} + b x + c = - 3$ 有两个不相等的实数根；⑤不等式 $m x + n > a x^{2} + b x + c$ 的解集为 $1 < x < 4$ ．上述五个结论中，其中正确的结论是（填写序号即可）．

查看试题解析

三、解答题

16. 计算： $| - \sqrt{3} | - (π - 2)^{0} + (\frac{1}{3})^{- 1} - 4 t a n 45 °$ ．

查看试题解析
17. 先化简，再求值：（ $\frac{x}{x^{2} + x}$ -1）÷ $\frac{x^{2} - 1}{x^{2} + 2 x + 1}$ ，其中x=2．

查看试题解析
18. 如图，在平行四边形ABCD中，点E、F在对角线BD上，且BE＝DF．求证：

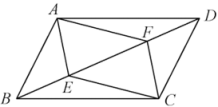(1)、△ABE≌△CDF；

(2)、四边形AECF是平行四边形．

查看试题解析

19. 国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》指出，要加强中小学生作业、睡眠、手机、读物、体质管理.某校数学社团成员采用随机抽样的方法，抽取了八年级部分学生，对他们一周内平均每天的睡眠时间

t

（单位：

h

）进行了调查，将数据整理后得到下列不完整的统计图表：

组别	睡眠时间分组	频数	频率
$A$	$t < 6$	4	0.08
$B$	$6 \leq t < 7$	8	0.16
$C$	$7 \leq t < 8$	10	$a$
$D$	$8 \leq t < 9$	21	0.42
$E$	$t \geq 9$	$b$	0.14

请根据图表信息回答下列问题：

(1)、频数分布表中，

a =

，

b =

；

(2)、扇形统计图中，

C

组所在扇形的圆心角的度数是

°

；

(3)、请估算该校600名八年级学生中睡眠不足7小时的人数；

(4)、研究表明，初中生每天睡眠时长低于7小时，会严重影响学习效率.请你根据以上调查统计结果，向学校提出一条合理化的建议.

查看试题解析

20. 为落实“垃圾分类回收，科学处理”的政策，某花园小区购买A、B两种型号的垃圾分类回收箱20只进行垃圾分类投放，共支付费用4320元．A、B型号价格信息如表：
型号
价格
A型
200元/只
B型
240元/只

(1)、请问小区购买A型和B型垃圾回收箱各多少只？

(2)、因受到居民欢迎，准备再次购进A、B两种型号的垃圾分类回收箱共40只，其中A类的数量不大于 B 类的数量的2倍．求购买多少只A 类回收箱支出的费用最少，最少费用是多少元？

查看试题解析
21. 某班同学在一次综合实践课上，测量校园内一棵树的高度．如图，测量仪在A处测得树顶D的仰角为45°，C处测得树顶D的仰角为37°（点A，B，C在一条水平直线上），已知测量仪高度AE＝CF＝1.6米，AC＝28米，求树BD的高度（结果保留小数点后一位．参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）．

查看试题解析
22. 如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC，AB于点E，F．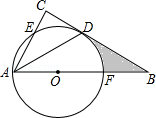

(1)、试判断直线BC与⊙O的位置关系，并说明理由；

(2)、若BD=2 $\sqrt{3}$ ，BF=2，求阴影部分的面积（结果保留π）．

查看试题解析
23. 如图，抛物线与x轴交于A、B两点，与y轴交于点C，且 $O A = 2$ ， $O B = 4$ ， $O C = 8$ ，抛物线的对称轴与直线BC交于点M，与x轴交于点N．

(1)、求抛物线的解析式；

(2)、若点P是对称轴上的一个动点，是否存在以P、C、M为顶点的三角形与 $△ M N B$ 相似？若存在，求出点P的坐标，若不存在，请说明理由．

(3)、点Q是抛物线上位于x轴上方的一点，点R在x轴上，是否存在以点Q为直角顶点的等腰 $R t △ C Q R$ ？若存在，求出点Q的坐标，若不存在，请说明理由．

查看试题解析

型号	价格
A型	200元/只
B型	240元/只