山西省太原市2023年中考二模数学试题
试卷更新日期:2023-06-21 类型:中考模拟
一、单选题
-
1. 在 , 1, , 0四个数中,绝对值最小的数是( )A、0 B、1 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 不等式组的解集是( )A、 B、 C、 D、4. 北京时间5月11日5时16分,天舟六号货运飞船成功对接于中国空间站天和核心舱后向端口.已知中国空间站在宇宙中的飞行速度为公里/秒,那么它飞行120分钟的路程为( )
 A、公里 B、公里 C、公里 D、公里5. 用6个大小相同的小立方体组成如图所示的几何体,该几何体主视图,俯视图,左视图的面积分别记作 , , , 则 , , 的大小关系是( )
A、公里 B、公里 C、公里 D、公里5. 用6个大小相同的小立方体组成如图所示的几何体,该几何体主视图,俯视图,左视图的面积分别记作 , , , 则 , , 的大小关系是( ) A、 B、 C、 D、6. 利用课后服务时间,同学们在操场上进行实地测量.如图,在处测得建筑物在南偏西的方向上,在处测得建筑物在南偏西的方向上.在建筑物处测得A,B两处的视角的度数为( )
A、 B、 C、 D、6. 利用课后服务时间,同学们在操场上进行实地测量.如图,在处测得建筑物在南偏西的方向上,在处测得建筑物在南偏西的方向上.在建筑物处测得A,B两处的视角的度数为( ) A、 B、 C、 D、7. 如图,正五边形内接于 , 点F是上的动点,则的度数为( )
A、 B、 C、 D、7. 如图,正五边形内接于 , 点F是上的动点,则的度数为( )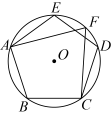 A、60° B、72° C、144° D、随着点的变化而变化8. 甲、乙、丙、丁四名同学围坐在一起商讨问题.如图是丙的座位,另外三人随机坐到①、②、③的任一个座位上.则甲和丁相邻的概率是( )
A、60° B、72° C、144° D、随着点的变化而变化8. 甲、乙、丙、丁四名同学围坐在一起商讨问题.如图是丙的座位,另外三人随机坐到①、②、③的任一个座位上.则甲和丁相邻的概率是( )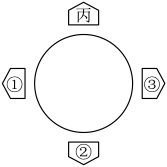 A、 B、 C、 D、9. 如图,在平面直角坐标系中,矩形的顶点A和C分别落在y轴与x轴的正半轴上, , . 若直线把矩形面积两等分,则b的值等于( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,矩形的顶点A和C分别落在y轴与x轴的正半轴上, , . 若直线把矩形面积两等分,则b的值等于( )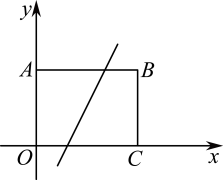 A、5 B、2 C、 D、10. 如图,在中, , , , 点为边上一点,点在的延长线上, . 若四边形是平行四边形,连接 , , 则图中阴影部分的面积为( )
A、5 B、2 C、 D、10. 如图,在中, , , , 点为边上一点,点在的延长线上, . 若四边形是平行四边形,连接 , , 则图中阴影部分的面积为( )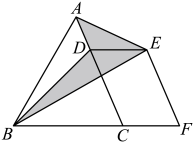 A、24 B、12 C、8 D、6
A、24 B、12 C、8 D、6二、填空题
-
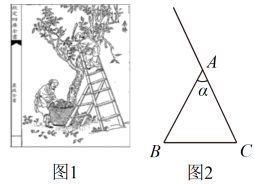
11. 化简 的结果是.12. 如图1是《农政全书》中记载有用于采桑的桑梯,图2是示意图.已知米,与的张角为 , 为固定张角大小的绳索.为保证作业安全,的取值范围大于等于且小于 , 则的取值范围是 .
 13. 在小明同学的笔记本中记录了求算术平方根近似值的一种方法,如 . 用他记录的这种方法,求得的近似值为 .14. 现有颗外观和大小都完全相同的小球,已知颗球的质量相等,另外一颗球的质量略大一些.小颖想用一架托盘天平称出这颗质量较大的球.她思考后发现最少称次就一定能找出这颗球,则的值等于 .
13. 在小明同学的笔记本中记录了求算术平方根近似值的一种方法,如 . 用他记录的这种方法,求得的近似值为 .14. 现有颗外观和大小都完全相同的小球,已知颗球的质量相等,另外一颗球的质量略大一些.小颖想用一架托盘天平称出这颗质量较大的球.她思考后发现最少称次就一定能找出这颗球,则的值等于 . 15. 如图,在中, , , 平分交于点D,点E在上, , 点F为的中点.若 , 则的长为 .
15. 如图,在中, , , 平分交于点D,点E在上, , 点F为的中点.若 , 则的长为 .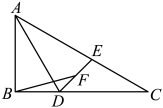
三、解答题
-
16.(1)、计算:;(2)、解方程: .17. 如图,在凹四边形中, , , , 求的度数.
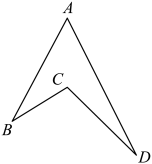
下面是学习小组的同学们交流时得到的解决问题的三种方法:
方法一:作射线AC;
方法二:延长BC交AD于点E;
方法三:连接BD.
请选择上述一种方法,求的度数.
18. 据携程发布的《年“五一”出游数据报告》,太原和济南、苏州、天津等凭借超强周边吸引力,上榜“五一”全国最强周边旅游“吸金力”前十名.为了解“五一”期间我市旅游的消费情况,从甲、乙两个旅游景点的游客中各随机抽取了人,获得了这些游客当天消费额(单位:元)的数据,并对数据进行整理、描述和分析.下面给出部分信息:a.甲旅游景点游客消费额的数据的频数分布直方图如下:
数据分成6组: , , , , , .
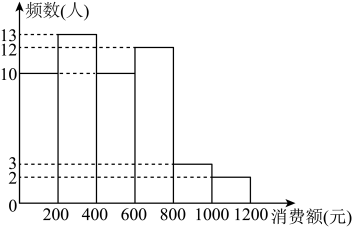
b.甲旅游景点游客消费额的数据在这一组的是:
c.甲、乙两个旅游景点游客消费额的数据的平均数、中位数如下:
消费额(元)
旅游景点
平均数
中位数
甲旅游景点
390
m
乙旅游景点
410
…
根据以上信息,回答下列问题:
(1)、表中m的值为 .(2)、一名被调查的游客当天的消费额为元,在他所去的旅游景点,他的消费额超过了一半以上的被调查的游客,那么他是哪个旅游景点的游客?请说明理由;(3)、若乙旅游景点当天的游客人数为人,估计乙旅游景点这天游客的消费总额.19. 如图1是一辆高空作业升降车在某次工作时的实景图,图2是它的示意图.已知点A,B,C,D,E,F,G在同一平面内,四边形为矩形,点B,C在地面l上, , 是可以伸缩的起重臂,转动点E到l的距离为2米.当米,米, , 时,求操作平台G到l的距离.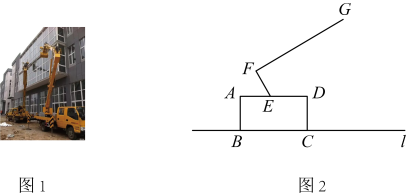 20. 太原的五月是月季的狂欢,滨河路上月季花扮靓道路两侧,形成了“绿染龙城,花满并州”的景观效果.市林业局将如图所示的一块长80米,宽40米的矩形空地分成五块小矩形区域,建成月季花种植基地.一块正方形区域为育苗区,一块矩形区域为存储区,其它区域分别种植风花月季,藤本月季和树桩月季.已知存储区的一边与育苗区的宽相等,另一边长为20米,风花月季、藤本月季和树桩月季每年每平方米的产值分别为200元、300元和400元.
20. 太原的五月是月季的狂欢,滨河路上月季花扮靓道路两侧,形成了“绿染龙城,花满并州”的景观效果.市林业局将如图所示的一块长80米,宽40米的矩形空地分成五块小矩形区域,建成月季花种植基地.一块正方形区域为育苗区,一块矩形区域为存储区,其它区域分别种植风花月季,藤本月季和树桩月季.已知存储区的一边与育苗区的宽相等,另一边长为20米,风花月季、藤本月季和树桩月季每年每平方米的产值分别为200元、300元和400元.
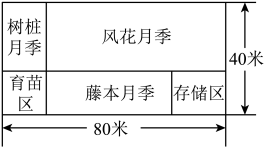 (1)、如果风花月季与藤本月季每年的产值相等,求育苗区的边长;(2)、如果风花月季种植面积与育苗区面积的差不超过2120平方米,求这三种月季花每年总产值的最大值.21. 阅读与思考
(1)、如果风花月季与藤本月季每年的产值相等,求育苗区的边长;(2)、如果风花月季种植面积与育苗区面积的差不超过2120平方米,求这三种月季花每年总产值的最大值.21. 阅读与思考下面是小宇同学的一篇日记,请仔细阅读并完成相应的任务.
在物理活动课上,我们“博学”小组的同学,参加了一次“探究电功率P与电阻R之间的函数关系”的活动.

第一步,实验测量.根据物理知识,改变电阻R的大小,通过测量电路中的电流,计算电功率P.
第二步,整理数据.
…
3
6
9
12
15
…
…
3
1.5
1
0.75
0.7
…
第三步,描点连线.以R的数值为横坐标,对应P的数值为纵坐标在平面直角坐标系中描出以表中数值为坐标的各点,并用光滑的曲线顺次连接这些点.
在数据分析时,我发现一个数据有错误,重新测量计算后,证明了我的猜想正确,并修改了表中这个数据.实验结束后,大家都有很多收获,每人都撰写了日记.
任务:
 (1)、表格中错误的数据是 , P与R的函数表达式为;(2)、在平面直角坐标系中,画出P与R的函数图象;(3)、结合图象,直接写出P大于6W时R的取值范围.22. 综合与实践
(1)、表格中错误的数据是 , P与R的函数表达式为;(2)、在平面直角坐标系中,画出P与R的函数图象;(3)、结合图象,直接写出P大于6W时R的取值范围.22. 综合与实践问题情境
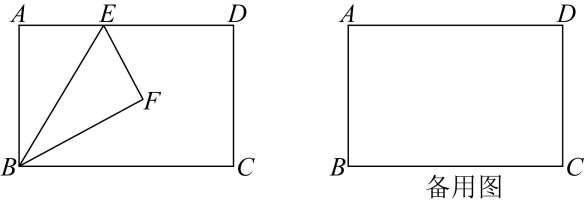
在矩形纸片中,点是边上一动点,连接 , 将沿折叠得到 , 并展开铺平.
 (1)、 实践操作
(1)、 实践操作在图中,过点作 , 垂足为点 , 交于点(要求:尺规作图,保留痕迹,不写作法);
(2)、 猜想证明在(1)所作的图形中连接 , 猜想并证明与之间的关系;
(3)、 问题解决已知 , , 沿所在直线折叠矩形纸片,折痕交矩形纸片的边于点 . 当时,求的长.
23. 综合与探究如图,抛物线与x轴交于和两点,与y轴交于点C,连接AC,BC.
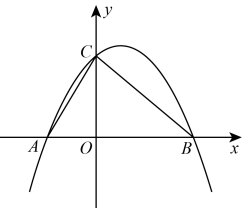
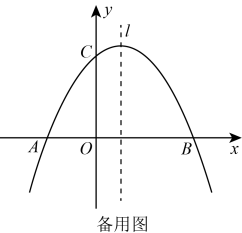 (1)、求抛物线的函数表达式;(2)、设点D在第一象限,且 , 求点D的坐标;(3)、点A绕抛物线的对称轴上一点P顺时针旋转90°恰好与点C重合,将沿x轴平移得到 , 点A,C,P的对应点分别为点 , , . 在抛物线上是否存在点E,使得以 , , , E为顶点的四边形是平行四边形?若存在,直接写出点E的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、设点D在第一象限,且 , 求点D的坐标;(3)、点A绕抛物线的对称轴上一点P顺时针旋转90°恰好与点C重合,将沿x轴平移得到 , 点A,C,P的对应点分别为点 , , . 在抛物线上是否存在点E,使得以 , , , E为顶点的四边形是平行四边形?若存在,直接写出点E的坐标;若不存在,请说明理由.