山西省吕梁市孝义市2023年中考三模数学试题
试卷更新日期:2023-06-21 类型:中考模拟
一、单选题
-
1. 的相反数是 ( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 近日,某校组织“自然资源文化创意大赛”,旨在宣传“新时代、美自然、好生活”,大赛分为“平面类”、“视觉类”、“实物类”三个竞赛单元,各单元按成绩由高到低,分别设立金奖5名、银奖10名、铜奖15名、优秀奖30名.甲同学参加了“视觉类”竞赛,并且竞赛成绩进入了前30名,该同学想知道自己能否至少获得银奖,需比较自己的成绩与前30名同学成绩的( )A、平均数 B、众数 C、中位数 D、方差4. 如图是一个正方体的展开图,在原正方体中,与“祝”字所在面相对的面上的汉字是( )
 A、考 B、试 C、成 D、功5. 某商店经销一种品牌的空气炸锅,其中某一型号的空气炸锅的进价为每台元,商店将进价提高30%后作为零售价销售,一段时间后,商店又按零售价的8折销售,这时该型号空气炸锅的零售价为( )A、元 B、元 C、元 D、元6. 如图,在中,点是的中点,对角线 , 相交于点 , 连接 , 若的周长是10,则的周长为( )
A、考 B、试 C、成 D、功5. 某商店经销一种品牌的空气炸锅,其中某一型号的空气炸锅的进价为每台元,商店将进价提高30%后作为零售价销售,一段时间后,商店又按零售价的8折销售,这时该型号空气炸锅的零售价为( )A、元 B、元 C、元 D、元6. 如图,在中,点是的中点,对角线 , 相交于点 , 连接 , 若的周长是10,则的周长为( ) A、3 B、5 C、6 D、77. 如图,在矩形纸片中, , , 点是上一点,点是上一点,将矩形沿折叠,使点的对应点正好落在的中点处,则的长为( )
A、3 B、5 C、6 D、77. 如图,在矩形纸片中, , , 点是上一点,点是上一点,将矩形沿折叠,使点的对应点正好落在的中点处,则的长为( )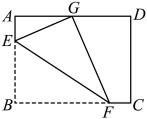 A、 B、 C、2 D、38. 如图,在平面直角坐标系中,点为坐标原点,菱形的顶点正好在反比例函数的图象上,点的坐标为 , 则的值为( )
A、 B、 C、2 D、38. 如图,在平面直角坐标系中,点为坐标原点,菱形的顶点正好在反比例函数的图象上,点的坐标为 , 则的值为( )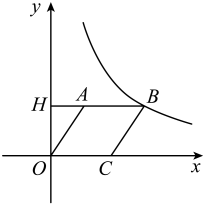 A、12 B、16 C、24 D、329. 如图,为半圆的直径,垂直平分半径 , 垂直平分半径 , 若 , 则图中阴影部分的面积等于( )
A、12 B、16 C、24 D、329. 如图,为半圆的直径,垂直平分半径 , 垂直平分半径 , 若 , 则图中阴影部分的面积等于( ) A、 B、 C、 D、10. 如图,矩形内接于 , 过点作的切线分别与的延长线交于点 , 与的延长线交于点 . 若 , , 则的长度为( )
A、 B、 C、 D、10. 如图,矩形内接于 , 过点作的切线分别与的延长线交于点 , 与的延长线交于点 . 若 , , 则的长度为( ) A、 B、 C、5 D、
A、 B、 C、5 D、二、填空题
-
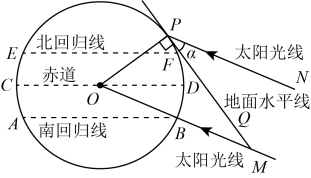
11. 化简的结果是 .12. 不等式组的解集是 .13. 现有两个不透明的盒子,其中一个装有标号分别为1,2的两张卡片,另一个装有标号分别为1,2,3的三张卡片,卡片除标号外其他均相同.若从两个盒子中各随机抽取一张卡片,则两张卡片标号恰好都是奇数的概率是 .14. 如图所示是地球截面图,其中 , 分别表示南回归线和北回归线,表示赤道,点表示太原市的位置.现已知地球南回归线的纬度是南纬 , 太原市的纬度是北纬 , 而冬至正午时,太阳光直射南回归线(光线的延长线经过地心),则太原市冬至正午时,太阳光线与地面水平线的夹角的度数是 .
 15. 如图,在正方形中,为的中点,将绕点顺时针方向旋转得到 , 分别连接 , , 且与交于点 , 若 , 则的长度为 .
15. 如图,在正方形中,为的中点,将绕点顺时针方向旋转得到 , 分别连接 , , 且与交于点 , 若 , 则的长度为 .
三、解答题
-
16.(1)、(2)、解方程:17. 已知:如图,点 , 在线段上, , , . 求证: .
 18. “谷子冬播夏收”是近年来农业种植的新技术之一,该技术打破了以往谷子在晚春进行播种的传统,在冬天或者早春进行播种,播种时铺上全生物降解渗水地膜(如左图),能最大限度地保证土壤中的水分不被蒸发,达到“秋雨冬储春夏用”的效果.2022年某农科所种植谷子50亩进行新旧技术对比试验,共收获谷子22000千克,经过对比发现,采用“冬播夏收”技术种植的谷子,平均亩产量比采用传统技术种植的谷子多25%.现已知传统技术种植的谷子平均每亩产量为400千克.
18. “谷子冬播夏收”是近年来农业种植的新技术之一,该技术打破了以往谷子在晚春进行播种的传统,在冬天或者早春进行播种,播种时铺上全生物降解渗水地膜(如左图),能最大限度地保证土壤中的水分不被蒸发,达到“秋雨冬储春夏用”的效果.2022年某农科所种植谷子50亩进行新旧技术对比试验,共收获谷子22000千克,经过对比发现,采用“冬播夏收”技术种植的谷子,平均亩产量比采用传统技术种植的谷子多25%.现已知传统技术种植的谷子平均每亩产量为400千克. (1)、求该农科所采用“传统技术”和“冬播夏收”技术各种植谷子多少亩?(2)、该农科所将收获的谷子加工成小米后,一部分采用“线上直播带货”的方式进行销售,销售价格为8元/千克,其余部分在实体店进行售卖,售卖价格为10元/千克.已知每1千克谷子能加工成0.8千克的小米,则该农科所要想销售完这批小米后,销售额不低于156000元,求该农科所最多将多少千克的小米以“线上直播带货”的方式进行销售?19. 2023年5月18日-21日,第七届世界智能大会在天津市举行,本届大会的主题是“智行天下,能动未来”.大会举办期间,某初中计划组织全校学生参观本届大会智能科技展的5个主题展区,主题分别是“人工智能”、“5G+工业互联网”、“智能交通”、“智慧生活”、“数字健康”,为了解同学们的参展意向、学校随机抽取了七年级的部分学生进行了问卷调查(调查问卷如下图所示),所有问卷全部收回,并将调查结果绘制成如下所示的统计图(均不完整).
(1)、求该农科所采用“传统技术”和“冬播夏收”技术各种植谷子多少亩?(2)、该农科所将收获的谷子加工成小米后,一部分采用“线上直播带货”的方式进行销售,销售价格为8元/千克,其余部分在实体店进行售卖,售卖价格为10元/千克.已知每1千克谷子能加工成0.8千克的小米,则该农科所要想销售完这批小米后,销售额不低于156000元,求该农科所最多将多少千克的小米以“线上直播带货”的方式进行销售?19. 2023年5月18日-21日,第七届世界智能大会在天津市举行,本届大会的主题是“智行天下,能动未来”.大会举办期间,某初中计划组织全校学生参观本届大会智能科技展的5个主题展区,主题分别是“人工智能”、“5G+工业互联网”、“智能交通”、“智慧生活”、“数字健康”,为了解同学们的参展意向、学校随机抽取了七年级的部分学生进行了问卷调查(调查问卷如下图所示),所有问卷全部收回,并将调查结果绘制成如下所示的统计图(均不完整).

“第七届世界智能大会”智能科技展
参观意向调查问卷
请在下列选项中选择您有参观意向的选项,在其后“[ ]”内打“√”(只能选择其中的一项),非常感谢您的合作.
A.人工智能[ ]
B.5G+工业互联网[ ]
C.智能交通[ ]
D.智慧生活[ ]
E数字健康[ ]
请根据上面的信息,解答下列问题:
(1)、本次调查所抽取的学生人数有人,所调查的学生中选择“C.智能交通”的学生人数占调查总人数的%.(2)、请把条形统计图补充完整.(3)、已知该初中总人数为1200人,小明根据调查结果,估计全校参观意向为“人工智能”的学生人数约为:人.你认为小明估计的结果是否合理?请说明理由.20. 山西博物院是我省综合性博物馆之一,其主馆造型如斗似鼎,四翼舒展,诠释了“如鸟斯革,如翚斯飞”的审美取向.某校“综合实践”小组在项目化学习中,对主馆进行了实地测量,图2是测量示意图.他们在地面上的点测得主馆顶部的仰角为 , 在台阶顶部处测得主馆顶部的仰角为 , 经过对每个台阶的高度与宽度进行测量,确定台阶顶部到地面的高度为12米,台阶底部与顶部之间的水平距离为30米.现已知台阶顶部平台与地面平行.请根据以上数据,求出主馆顶部到地面的垂直高度是多少米?(参考数据: , , )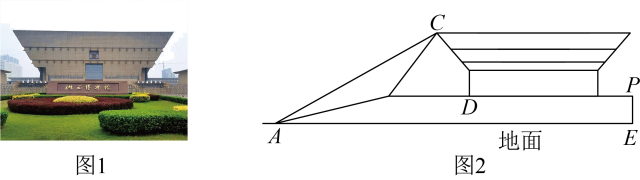 21. 阅读与思考:下面是小宇同学写的一篇数学小论文,请你认真阅读并完成相应学习任务:
21. 阅读与思考:下面是小宇同学写的一篇数学小论文,请你认真阅读并完成相应学习任务:怎样作直角三角形的内接正方形
如果一个正方形的四个顶点都在直角三角形的三条边上,我们把这样的正方形叫做该直角三角形的内接正方形.那么,怎样作出一个直角三角形的内接正方形呢?我们可以用如下方法:
如图1,在中, , 作的角平分线,交斜边于点;然后过点 , 分别作 , 的垂线,垂足分别为 , , 则 . (依据1)
容易证明四边形是正方形.

用上面方法所作出的正方形,有一个顶点恰好是直角三角形的直角顶点.
如图2,如果的内接正方形的一边恰好在斜边上,我就可用如下方法,
第一步:过直角顶点作 , 垂足为;
第二步,延长到 , 使得 , 连接;
第三步:作的平分线,交于点;
第四步:过点分别作 , 的垂线,垂足分别为 , , 交于点 , 的延长线交交于;
第五步:分别过点 , 作的垂线,垂足分别为 , .
则四边形就是的内接正方形,并且恰好在该直角三角形的斜边上.
理由如下:易证四边形是正方形, .
∵ , ∴ , . (依据2)
∴;
学习任务:
(1)、材料中画横线部分的依据分别是:依据1:;依据2: .
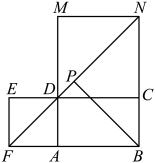
(2)、请完成图2说理过程的剩余部分.(3)、分析图2的作图过程,不难看出是将图2转化成图1去完成的,即先做图形 , 再将正方形转化为正方形 , 转化的过程可以看作是一种图形变换,这种图形变换是____.(填出字母代号即可).A、旋转 B、平移 C、轴对称22. 综合与实践问题情境:数学课上,老师提出如下问题:如图,四边形是矩形,分别以 , 为边,在矩形外侧作正方形和(点 , , 在同一直线上,点 , , 在同一直线上).连接 , 取的中点 , 连接 .
求证: , .
解决问题:
(1)、请你解答老师提出的问题.(2)、受到老师所提问题的启发,“兴趣小组”又提出了一个新问题:如图,若四边形是平行四边形 , 其余条件保持不变,则老师所提问题的结论是否保持不变?请你说明理由. (3)、“智慧小组”所提的问题是:如图,四边形是菱形,分别以 , 为边,在菱形外侧作正方形和 . 连接并延长,交于点 . 若 , , 求的长.请你思考该问题,并直接写出结果.
(3)、“智慧小组”所提的问题是:如图,四边形是菱形,分别以 , 为边,在菱形外侧作正方形和 . 连接并延长,交于点 . 若 , , 求的长.请你思考该问题,并直接写出结果.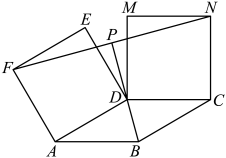 23. 综合与探究:
23. 综合与探究:如图,已知抛物线与x轴交于A,B两点(点A在点B的左边),与y轴交于点C.直线BC与抛物线的对称轴交于点E.将直线BC沿射线CO方向向下平移n个单位,平移后的直线与直线AC交于点F,与抛物线的对称轴交于点D.
 (1)、求出点A,B,C的坐标,并直接写出直线AC,BC的解析式;(2)、当是以BC为斜边的直角三角形时,求出n的值;(3)、直线BC上是否存在一点P,使以点D,E,F,P为顶点的四边形是菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.
(1)、求出点A,B,C的坐标,并直接写出直线AC,BC的解析式;(2)、当是以BC为斜边的直角三角形时,求出n的值;(3)、直线BC上是否存在一点P,使以点D,E,F,P为顶点的四边形是菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.