天津市南开区2023年中考三模数学试题
试卷更新日期:2023-06-21 类型:中考模拟
一、单选题
-
1. 计算:5+(-7)=( )A、2 B、-2 C、12 D、-122. 的值等于( )A、 B、1 C、 D、3. 将4370000用科学记数法表示为( )A、 B、 C、 D、4. 下列四个甲骨文中是轴对称图形是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图是由7块相同的小正方体组成的立体图形,它的主视图是( )
5. 如图是由7块相同的小正方体组成的立体图形,它的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 估计 的值在( )A、 和 之间 B、 和 之间 C、 和 之间 D、 和 之间7. 化简的结果为( )A、1 B、 C、2 D、8. 若点在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、9. 方程的根是 , , 则的值为( )A、22 B、 C、 D、2610. 如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,则点C的坐标( )
6. 估计 的值在( )A、 和 之间 B、 和 之间 C、 和 之间 D、 和 之间7. 化简的结果为( )A、1 B、 C、2 D、8. 若点在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、9. 方程的根是 , , 则的值为( )A、22 B、 C、 D、2610. 如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,则点C的坐标( )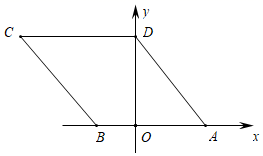 A、(﹣3,4) B、(﹣2,3) C、(﹣5,4) D、(5,4)11. 如图,将直角沿斜边的方向平移到的位置,交于点G, , , 的面积为4,下列结论错误的是( )
A、(﹣3,4) B、(﹣2,3) C、(﹣5,4) D、(5,4)11. 如图,将直角沿斜边的方向平移到的位置,交于点G, , , 的面积为4,下列结论错误的是( ) A、 B、平移的距离是4 C、 D、四边形的面积为1612. 如图,函数的图象过点和 . 有下列结论:①;②;③关于x的方程必有两个不等的实数根;其中正确结论有( )
A、 B、平移的距离是4 C、 D、四边形的面积为1612. 如图,函数的图象过点和 . 有下列结论:①;②;③关于x的方程必有两个不等的实数根;其中正确结论有( ) A、0个 B、1个 C、2个 D、3个
A、0个 B、1个 C、2个 D、3个二、填空题
-
13. 计算: .14. 计算: .15. 在一个不透明的布袋中装有18个白球和9个黑球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,摸到白球的概率是 .16. 请选择一个你喜欢的数值m,使相应的一次函数的值随着x值的增大而减小,m的值可以是 .17. 如图,中, , , 点D,E分别在边 , 上,且 , 连接 , 点M是的中点,点N是BC的中点,线段MN的长为 .
 18. 已知B,C是平面直角坐标系中与x轴平行且距离x轴1个单位长度的直线上的两个动点(点B在点C左侧),且 , 若有点和点 , 则当的值最小时,点B的坐标为 .
18. 已知B,C是平面直角坐标系中与x轴平行且距离x轴1个单位长度的直线上的两个动点(点B在点C左侧),且 , 若有点和点 , 则当的值最小时,点B的坐标为 .三、解答题
-
19. 解不等式组
请按下列步骤完成解答:
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来; (4)、原不等式组的解集为 .20. 在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位;),绘制出统计图①和图②.请根据相关信息,解答下列问题:
(4)、原不等式组的解集为 .20. 在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位;),绘制出统计图①和图②.请根据相关信息,解答下列问题: (1)、本次参加男子跳高初赛的运动员人数为;图①中a的值为;(2)、求统计的这组初赛成绩数据的平均数、众数和中位数;21. 内接于 , 直线与相切于点D,与相交于点E, .
(1)、本次参加男子跳高初赛的运动员人数为;图①中a的值为;(2)、求统计的这组初赛成绩数据的平均数、众数和中位数;21. 内接于 , 直线与相切于点D,与相交于点E, . (1)、如图1,若 , 求的大小;(2)、如图2,若是的直径, , , 连接 , 求的长.22. 如图,在一次联合反潜演习中,军舰A测得潜艇C的俯角为31°;位于军舰A正上方500m的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出潜艇C离开海平面的下潜深度(结果保留整数)
(1)、如图1,若 , 求的大小;(2)、如图2,若是的直径, , , 连接 , 求的长.22. 如图,在一次联合反潜演习中,军舰A测得潜艇C的俯角为31°;位于军舰A正上方500m的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出潜艇C离开海平面的下潜深度(结果保留整数)( , , , , , , )
 23. 一天,一辆汽车从甲地出发前往乙地送货,途经服务区进行了短暂休息,到达乙地卸货后返回甲地.汽车返回时,仅用0.8小时便到达服务区,但并未停留,汽车距离甲地的路程s(千米)与行驶时间t(小时)之间的关系如下图的折线OABCDE所示:
23. 一天,一辆汽车从甲地出发前往乙地送货,途经服务区进行了短暂休息,到达乙地卸货后返回甲地.汽车返回时,仅用0.8小时便到达服务区,但并未停留,汽车距离甲地的路程s(千米)与行驶时间t(小时)之间的关系如下图的折线OABCDE所示:
根据图象信息,解答下列问题:
(1)、填表:行驶时间t(小时)
l
2
3.5
4.5
汽车距离甲地的路程s(千米)
120
200
(2)、填空:①整个过程中,汽车共行驶了千米,
②到达乙地后卸货所用的时长为小时;
③汽车从服务区到乙地的速度为千米/小时;
④汽车从乙地回到甲地的速度为千米/小时;
⑤a的值为;
(3)、当时,请直接写出s关于t的函数解析式.