天津市和平区2023年中考三模数学试题
试卷更新日期:2023-06-21 类型:中考模拟
一、单选题
-
1. 计算(-3)-9的结果等于( )A、6 B、-6 C、12 D、-122. 的值等于( )A、 B、 C、1 D、23. “全民行动,共同节约”,我国14亿人口如果都响应国家号召每人每年节约1度电,一年可节 约1 400 000 000度电,这个数用科学记数法表示,正确的是( )A、1.40×108 B、1.4×109 C、0.14×1010 D、1.4×10104. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图的是( )A、
 B、
B、 C、
C、 D、
D、 5. 下图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
5. 下图是一个由5个相同的正方体组成的立体图形,它的主视图是( )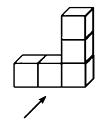 A、
A、 B、
B、 C、
C、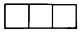 D、
D、 6. 估计的值在( )A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间7. 化简 的结果是( )A、 +1 B、 C、 D、8. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、9. 《孙子算经》中有一道题: “今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余尺;将绳子对折再量木条,木条剩余尺,问木条长多少尺?”如果设木条长尺,绳子长尺,可列方程组为( )A、 B、 C、 D、10. 如图,矩形的顶点 , , 顶点C在x轴的正半轴上.作如下操作:①对折矩形 , 使得与重合,得到折痕 , 把纸片展平;②再一次折叠纸片,使点A落在上,并使折痕经过点O,得折痕 , 同时,得到了线段 . 则点N的坐标是( )
6. 估计的值在( )A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间7. 化简 的结果是( )A、 +1 B、 C、 D、8. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、9. 《孙子算经》中有一道题: “今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余尺;将绳子对折再量木条,木条剩余尺,问木条长多少尺?”如果设木条长尺,绳子长尺,可列方程组为( )A、 B、 C、 D、10. 如图,矩形的顶点 , , 顶点C在x轴的正半轴上.作如下操作:①对折矩形 , 使得与重合,得到折痕 , 把纸片展平;②再一次折叠纸片,使点A落在上,并使折痕经过点O,得折痕 , 同时,得到了线段 . 则点N的坐标是( ) A、 B、 C、 D、11. 如图,将沿射线的方向平移,得到 , 再将绕点逆时针旋转一定角度后,得到 , 点的对应点为 , 点的对应点为点 , 则下列结论不一定正确的是( )
A、 B、 C、 D、11. 如图,将沿射线的方向平移,得到 , 再将绕点逆时针旋转一定角度后,得到 , 点的对应点为 , 点的对应点为点 , 则下列结论不一定正确的是( )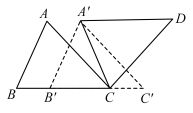 A、 B、 C、 D、平分12. 抛物线( , 为常数且)的对称轴为 , 过点和点 . 有下列结论:①;②对任意实数 , 都有;③若 , 则 . 其中,正确结论的个数是( )A、0 B、1 C、2 D、3
A、 B、 C、 D、平分12. 抛物线( , 为常数且)的对称轴为 , 过点和点 . 有下列结论:①;②对任意实数 , 都有;③若 , 则 . 其中,正确结论的个数是( )A、0 B、1 C、2 D、3二、填空题
-
13. 计算的结果等于 .14. 计算 的结果等于 .15. 不透明袋子中装有8个球,其中有5个红球、2个白球和1个黑球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是白球的概率是 .16. 若一次函数的图象经过点(1,3),且y随着x的增大而增大,则一次函数的解析式为(写出一个即可).17. 如图,在中, , , 点D是中点,E是边上一点,且 , 则的长等于 .
 18. 如图,在每个小正方形的边长为1的网格中,圆上的点在格点上,点在格点上,圆心在线段上,圆与网格线相交于点 , 过点作圆的切线与网格线交于点 .
18. 如图,在每个小正方形的边长为1的网格中,圆上的点在格点上,点在格点上,圆心在线段上,圆与网格线相交于点 , 过点作圆的切线与网格线交于点 . (1)、;(2)、过点作圆的切线,切点为(点不与点重合).请用无刻度的直尺,在如图所示的网格中,画出点 , 并简要说明点的位置是如何找到的(不要求证明) .
(1)、;(2)、过点作圆的切线,切点为(点不与点重合).请用无刻度的直尺,在如图所示的网格中,画出点 , 并简要说明点的位置是如何找到的(不要求证明) .三、解答题
-
19. 解不等式组
请结合题意填空,完成本题的解答.
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来: (4)、原不等式组的解集为 .20. 九年级研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计同学们一个月阅读课外书的数量.根据调查结果,绘制出如下的统计图①和图②.
(4)、原不等式组的解集为 .20. 九年级研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计同学们一个月阅读课外书的数量.根据调查结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)、本次抽取参与问卷的学生人数为 , 图①中m的值为;(2)、求统计的这组一个月阅读课外书数量数据的平均数、众数和中位数;(3)、全校共有学生1400名,根据样本数据,估计该校学生一个月阅读2本课外书的人数约为多少?21. 已知中, , 与相交于点D,过点D作的切线,交于点E. (1)、如图①,线段为的直径,若 , 求的大小;(2)、如图②,过圆心O,线段与相切于点F,若 , 且 , 求圆的半径和的长.22. 如图,某校数学兴趣小组要测量建筑物的高度,测角仪的高度为米.他们在点C测得楼顶A的仰角为 , 前行米到达F点,这时在点E处测得楼顶A的仰角为 , 求建筑物的高度(结果保留整数).参考数据: .
(1)、如图①,线段为的直径,若 , 求的大小;(2)、如图②,过圆心O,线段与相切于点F,若 , 且 , 求圆的半径和的长.22. 如图,某校数学兴趣小组要测量建筑物的高度,测角仪的高度为米.他们在点C测得楼顶A的仰角为 , 前行米到达F点,这时在点E处测得楼顶A的仰角为 , 求建筑物的高度(结果保留整数).参考数据: . 23. 在“看图说故事”活动中,某学习小组根据《龟兔赛跑》的故事绘制了函数图象.
23. 在“看图说故事”活动中,某学习小组根据《龟兔赛跑》的故事绘制了函数图象.
乌龟和兔子在笔直的公路上比赛,它们从同一地点同时出发后匀速向终点前进,兔子很快把乌龟远远甩在后头,骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是兔子加快速度追赶,最后还是输给了乌龟.图中的线段和折线分别表示乌龟和兔子的路程ym和时间x之间的对应关系.
请根据相关信息,解答下列问题:
(1)、填表:比赛时间
5
10
35
52
60
兔子所走的路程
200
550
(2)、填空:①赛跑中,兔子共睡了;
②乌龟追上兔子所用的时间为;
③兔子到达终点比乌龟晚了;
④在比赛过程中,龟和兔最多相距m.
(3)、当时,请直接写出兔子在赛跑过程y和x的函数解析式.24. 在平面直角坐标系中,O为原点,是直角三角形, , , 点 , 射线上有一个动点C,线段上有一个动点D,沿直线折叠 , 点B对应点为 , 轴. (1)、如图①,若点落x轴上,求点C的坐标;(2)、设 .
(1)、如图①,若点落x轴上,求点C的坐标;(2)、设 .①如图②,折叠后的与重叠部分为四边形,和分别与x轴交于P,Q两点,试用含t的式子表示的长,并直接写出t的取值范围;
②若与重叠部分的面积S,当时,求S的取值范围.(直接写出结果即可)
25. 已知抛物线( , 是常数)的顶点为P,与x轴相交于点A和点B,与y轴相交于点C.(1)、若 , A点坐标为 , 对称轴为直线 ,①求点P的坐标:
②将直线BC沿y轴向下平移个单位长度,并且与抛物线总有公共点,求n的取值范围;
(2)、若 , A点坐标为 , 对称轴为直线 , 在平面内有一个动点Q,当m为何值时,的最小值是?