山东省烟台市莱阳市2023年中考二模数学试题
试卷更新日期:2023-06-21 类型:中考模拟
一、单选题
-
1. 下列说法正确的是( )A、2的倒数是 B、3的相反数是 C、绝对值最小的数是1 D、0的相反数是02. 2023年2月24日,“逐梦寰宇问苍穹——中国载人航天工程三十年成就展”在中国国家博物馆开幕,系统展示了载人航天事业取得的跨越式发展和历史性成就.下列航天图标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 孙悟空是中国明代小说家吴承恩的著作《西游记》中的角色之一,它会七十二变、筋斗云,一个筋斗能翻十万八千里(1里).将十万八千里用科学记数法可表示为( )A、 B、 C、 D、5. 体育课上,体育老师随机抽取了某班10名男生的引体向上成绩,将这组数据整理后制成如下统计表,则关于这组数据下列说法正确的是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 孙悟空是中国明代小说家吴承恩的著作《西游记》中的角色之一,它会七十二变、筋斗云,一个筋斗能翻十万八千里(1里).将十万八千里用科学记数法可表示为( )A、 B、 C、 D、5. 体育课上,体育老师随机抽取了某班10名男生的引体向上成绩,将这组数据整理后制成如下统计表,则关于这组数据下列说法正确的是( )成绩/个
9
8
6
5
人数
2
3
3
2
A、方差是2.2 B、中位数是8 C、众数是8 D、平均数是86. 如图,一块直角三角板的斜边与量角器的直径重合,点D对应的刻度值为 , 则的度数为( ) A、 B、 C、 D、7. 甲、乙两种物质的溶解度y()与温度t()之间的对应关系如图所示,下列说法:①甲、乙两种物质的溶解度都随着温度的升高而增大;②当温度升高至时,甲的溶解度比乙的溶解度小;③当温度为时,甲、乙的溶解度都小于;④当温度为时,甲、乙的溶解度相同.其中正确结论的序号是( )
A、 B、 C、 D、7. 甲、乙两种物质的溶解度y()与温度t()之间的对应关系如图所示,下列说法:①甲、乙两种物质的溶解度都随着温度的升高而增大;②当温度升高至时,甲的溶解度比乙的溶解度小;③当温度为时,甲、乙的溶解度都小于;④当温度为时,甲、乙的溶解度相同.其中正确结论的序号是( ) A、①② B、①③ C、①③④ D、②④8. 如图所示的运算程序中,甲输入的x为 , 乙输入的x为 , 丙输入的x为 . 若 , 则输出结果相同的是( )
A、①② B、①③ C、①③④ D、②④8. 如图所示的运算程序中,甲输入的x为 , 乙输入的x为 , 丙输入的x为 . 若 , 则输出结果相同的是( )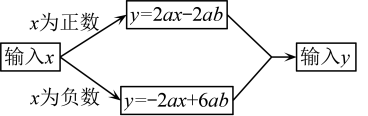 A、甲和乙 B、甲和丙 C、乙和丙 D、三人均不相同9. 自然界中存在许多斐波那契螺旋线图案.斐波那契螺旋线,也称“黄金螺旋线”,是根据斐波那契数1,1,2,3,5,8,13,……画出米的螺旋曲线.在平面直角坐标系中,依次以这组数为半径作的圆弧 , 得到一组螺旋线,连接 , 得到一组螺旋折线,如图所示.已知点的坐标分别为 , 则点的坐标为( )
A、甲和乙 B、甲和丙 C、乙和丙 D、三人均不相同9. 自然界中存在许多斐波那契螺旋线图案.斐波那契螺旋线,也称“黄金螺旋线”,是根据斐波那契数1,1,2,3,5,8,13,……画出米的螺旋曲线.在平面直角坐标系中,依次以这组数为半径作的圆弧 , 得到一组螺旋线,连接 , 得到一组螺旋折线,如图所示.已知点的坐标分别为 , 则点的坐标为( ) A、 B、 C、 D、10. 已知二次函数的部分图象如图所示,图象过点 , 对称轴为直线 , 下列结论:①;②;③;④若点在该函数图象上,则;⑤若方程的两根为和 , 且 , 则 . 其中正确的结论有( )
A、 B、 C、 D、10. 已知二次函数的部分图象如图所示,图象过点 , 对称轴为直线 , 下列结论:①;②;③;④若点在该函数图象上,则;⑤若方程的两根为和 , 且 , 则 . 其中正确的结论有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 枫叶一般呈掌状五裂型,裂片具有少数突出的齿.小明将一个枫叶标本放在平面直角坐标系中如图,表示叶片“顶”A,B两点的坐标分别为 , 则叶柄“底部”点C的坐标为 .
 12. 在螳螂的示意图中, , 是等腰三角形, , 则的度数是 .
12. 在螳螂的示意图中, , 是等腰三角形, , 则的度数是 .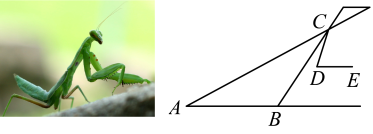 13. 图①是艺术家埃舍尔的作品,他将数学与绘画完美结合,在平面上创造出立体效果.图②是一个菱形,将图②截去一个边长为原来一半的菱形得到图③,用图③镶嵌得到图④,将图④着色后,再次镶嵌便得到图①,则图④中的度数是 .
13. 图①是艺术家埃舍尔的作品,他将数学与绘画完美结合,在平面上创造出立体效果.图②是一个菱形,将图②截去一个边长为原来一半的菱形得到图③,用图③镶嵌得到图④,将图④着色后,再次镶嵌便得到图①,则图④中的度数是 .


 14. 幻方历史悠久,传说最早出现在夏禹时代的“洛书”当中,根据幻方的相等关系设计出来一个“幻圆”,即大圆.小圆.横线.竖线上的四个数字加起来的和均相等.如图给出了部分数字,则幻圆中的值为 .
14. 幻方历史悠久,传说最早出现在夏禹时代的“洛书”当中,根据幻方的相等关系设计出来一个“幻圆”,即大圆.小圆.横线.竖线上的四个数字加起来的和均相等.如图给出了部分数字,则幻圆中的值为 . 15. 七巧板是古代中国劳动人民的发明,是一种古老的中国传统智力游戏,其历史至少可以追溯到公元前一世纪.小明将一个边长为4的正方形制作成一副如图1所示的七巧板,取出其中的六块,拼成了一个(如图2),则的对角线AC的长度为 .
15. 七巧板是古代中国劳动人民的发明,是一种古老的中国传统智力游戏,其历史至少可以追溯到公元前一世纪.小明将一个边长为4的正方形制作成一副如图1所示的七巧板,取出其中的六块,拼成了一个(如图2),则的对角线AC的长度为 .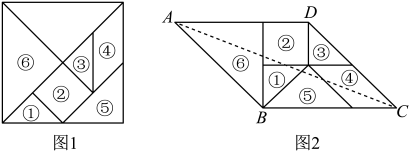 16. 如图1,在中, , 动点从点出发,以每秒1个单位的速度沿线段运动到点停止,同时动点从点出发,以每秒4个单位的速度沿折线运动到点停止.图2是点运动时,的面积与运动时间函数关系的图象,则的值是 .
16. 如图1,在中, , 动点从点出发,以每秒1个单位的速度沿线段运动到点停止,同时动点从点出发,以每秒4个单位的速度沿折线运动到点停止.图2是点运动时,的面积与运动时间函数关系的图象,则的值是 .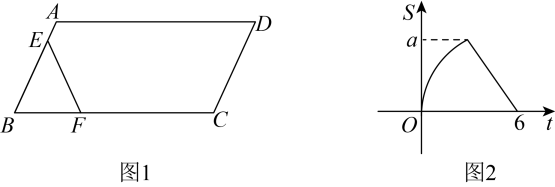
三、解答题
-
17. 计算:(1)、(2)、18. 如图,在中,点D、E分别是边的中点,点F在线段上, , 求的长度.
 19. 春暖花开正是郊游踏青的好时节.为开阔学生视野,一班的家委会准备利用周末组织该班学生参加郊游活动,计划在某商家采购A、B两种水果各600元,其中A种水果比B种水果多买20千克,该商家B种水果的单价是A种水果单价的1.5倍.(1)、求A、B两种水果的单价分别是多少元?(2)、经过家委会和商家协商,商家决定给该班购买的A、B两种水果进行优惠,将A、B两种水果都打8折,因此,家长将调整购买计划,购买A、B两种水果共150千克,但购买的总费用不能超过1500元,则至少购买A种水果多少千克?20. 某校九年级体育期末检测自选项目有篮球、跳绳、立定跳远,每个学生任选一项为自选考试项目.(1)、求学生甲与乙至少有一人自选篮球的概率;(2)、除自选项目以外,长跑为必考项目,校内体育活动表现是必查项目,学生甲与乙的期末体育各项成绩(百分制)的统计图表如图所示:
19. 春暖花开正是郊游踏青的好时节.为开阔学生视野,一班的家委会准备利用周末组织该班学生参加郊游活动,计划在某商家采购A、B两种水果各600元,其中A种水果比B种水果多买20千克,该商家B种水果的单价是A种水果单价的1.5倍.(1)、求A、B两种水果的单价分别是多少元?(2)、经过家委会和商家协商,商家决定给该班购买的A、B两种水果进行优惠,将A、B两种水果都打8折,因此,家长将调整购买计划,购买A、B两种水果共150千克,但购买的总费用不能超过1500元,则至少购买A种水果多少千克?20. 某校九年级体育期末检测自选项目有篮球、跳绳、立定跳远,每个学生任选一项为自选考试项目.(1)、求学生甲与乙至少有一人自选篮球的概率;(2)、除自选项目以外,长跑为必考项目,校内体育活动表现是必查项目,学生甲与乙的期末体育各项成绩(百分制)的统计图表如图所示:
考生
自选项目
长跑
校内体育活动
甲
95
100
95
乙
100
95
95
①补全条形统计图;
②如果期末体育考试成绩按照扇形统计图(图2)各项所占之比计算(百分制),请通过计算说明甲、乙两人谁的期末体育成绩高.
 21. 图1是一盏可调节台灯,图2为其平面示意图,固定底座与水平面垂直,为固定支撑杆,为可绕着点旋转的调节杆,若 , , , , , 求台灯灯体到水平面的距离.(结果精确到 , 参考数据: , , , , , )
21. 图1是一盏可调节台灯,图2为其平面示意图,固定底座与水平面垂直,为固定支撑杆,为可绕着点旋转的调节杆,若 , , , , , 求台灯灯体到水平面的距离.(结果精确到 , 参考数据: , , , , , ) 22. 如图,在 中, ,以斜边 上的中线 为直径作 ,与 交于点M,与 的另一个交点为E,过M作 ,垂足为N.
22. 如图,在 中, ,以斜边 上的中线 为直径作 ,与 交于点M,与 的另一个交点为E,过M作 ,垂足为N.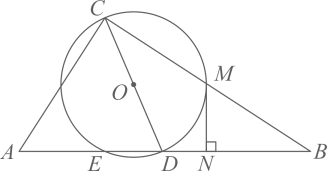 (1)、求证: 是 的切线;(2)、若 的直径为5, ,求 的长.23. 已知 , , 点C为射线上一动点(不与点B重合),关于的轴对称图形为 .
(1)、求证: 是 的切线;(2)、若 的直径为5, ,求 的长.23. 已知 , , 点C为射线上一动点(不与点B重合),关于的轴对称图形为 . (1)、如图1,当点D在射线上时,求证:四边形是菱形;(2)、如图2,当点D在射线 , 之间时,若点G为射线上一点,点C为的中点,连接交于点M, .
(1)、如图1,当点D在射线上时,求证:四边形是菱形;(2)、如图2,当点D在射线 , 之间时,若点G为射线上一点,点C为的中点,连接交于点M, .①求证:为直角三角形;
②求的长.
24. 如图,在平面直角坐标系中,抛物线(b、c为常数)的顶点坐标为 , 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,点C与点D关于x轴对称,连接 , 作直线 .
 (1)、求点A和点B的坐标;(2)、求证:;(3)、点P在抛物线上,点Q在直线上,当以点C、D、P、Q为顶点的四边形为平行四边形时,直接写出点Q的坐标.
(1)、求点A和点B的坐标;(2)、求证:;(3)、点P在抛物线上,点Q在直线上,当以点C、D、P、Q为顶点的四边形为平行四边形时,直接写出点Q的坐标.