河北省张家口市、保定市、石家庄市2023年中考六模数学试题
试卷更新日期:2023-06-21 类型:中考模拟
一、单选题
-
1. 下列整式中,是二次单项式的是( )A、 B、 C、 D、2. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( )
 A、 B、1 C、 D、23. 下列各式中,化简后能与合并的是( ).A、 B、 C、 D、4. 如图,现有一把直尺和一块三角尺,其中 , , AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到 , 点对应直尺的刻度为0,则四边形的面积是( )
A、 B、1 C、 D、23. 下列各式中,化简后能与合并的是( ).A、 B、 C、 D、4. 如图,现有一把直尺和一块三角尺,其中 , , AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到 , 点对应直尺的刻度为0,则四边形的面积是( )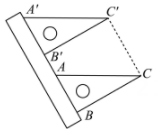 A、96 B、 C、192 D、5. 下面算式与的值相等的是( )A、 B、 C、 D、6. 如图,圆柱的底面直径为AB,高为AC.一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A、96 B、 C、192 D、5. 下面算式与的值相等的是( )A、 B、 C、 D、6. 如图,圆柱的底面直径为AB,高为AC.一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )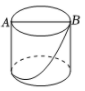 A、
A、 B、
B、 C、
C、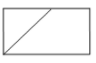 D、
D、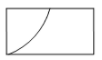 7. 解方程 ,以下去括号正确的是( )A、 B、 C、 D、8. 如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5分),则所打分数的众数为( )
7. 解方程 ,以下去括号正确的是( )A、 B、 C、 D、8. 如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5分),则所打分数的众数为( ) A、5分 B、4分 C、3分 D、45%9. 不能被下列数整除的是( )A、 B、 C、 D、10. 如图,内接于⊙ , 连接 , 则( )
A、5分 B、4分 C、3分 D、45%9. 不能被下列数整除的是( )A、 B、 C、 D、10. 如图,内接于⊙ , 连接 , 则( )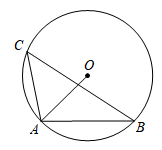 A、 B、 C、 D、11. 若分式 的运算结果为 ,则在 中添加的运算符号为( )A、+ B、- C、+或÷ D、-或×12. 如图,在正方形网格中,与位似,则下列说法正确的是( )
A、 B、 C、 D、11. 若分式 的运算结果为 ,则在 中添加的运算符号为( )A、+ B、- C、+或÷ D、-或×12. 如图,在正方形网格中,与位似,则下列说法正确的是( ) A、位似中心是点 B、位似中心是点 C、位似比为 D、位似比为13. 如图,在平面直角坐标系中有 , , , 四个点,其中恰有三点在反比例函数的图象上.根据图中四点的位置,判断这四个点中不在函数的图象上的点是( )
A、位似中心是点 B、位似中心是点 C、位似比为 D、位似比为13. 如图,在平面直角坐标系中有 , , , 四个点,其中恰有三点在反比例函数的图象上.根据图中四点的位置,判断这四个点中不在函数的图象上的点是( )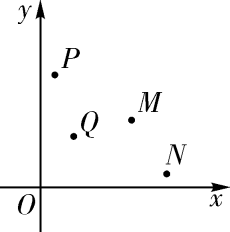 A、点 B、点 C、点 D、点14. 如图1,在边长为2的正六边形ABCDEF中,M是BC的中点,连接EM交AD于N点,若 , 则表示实数a的点落在数轴上(如图2)标有四段中的( )
A、点 B、点 C、点 D、点14. 如图1,在边长为2的正六边形ABCDEF中,M是BC的中点,连接EM交AD于N点,若 , 则表示实数a的点落在数轴上(如图2)标有四段中的( )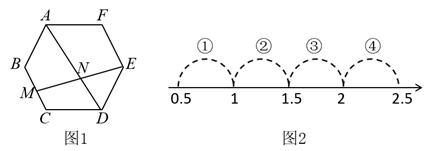 A、段① B、段② C、段③ D、段④15. 如图,中, , 点为各内角平分线的交点,过点作的垂线,垂足为 , 若 , , 则的长为( )
A、段① B、段② C、段③ D、段④15. 如图,中, , 点为各内角平分线的交点,过点作的垂线,垂足为 , 若 , , 则的长为( )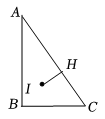 A、 B、 C、 D、16. 在证明勾股定理时,甲、乙两位同学分别设计了如下方案:
A、 B、 C、 D、16. 在证明勾股定理时,甲、乙两位同学分别设计了如下方案:甲
乙
如图,用四个全等的直角三角形拼成,其中四边形ABDE和四边形CFCH均是正方形,通过用两种方法表示正方形ABDE的面积来进行证明.
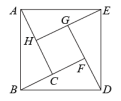
如图是两个全等的直角三角板ABC和直角三角板DEF,顶点F在BC边上,顶点C,D重合,通过用两种方法表示四边形ACBE的面积来进行证明.

对于甲、乙分别设计的两种方案,下列判断正确的是( )
A、甲、乙均对 B、甲对、乙不对 C、甲不对,乙对 D、甲、乙均不对二、填空题
-
17. 如图,直线 , , , 则 .
 18. 如图①,点 , , 是数轴上从左到右排列的三个点,分别对应的数为 , , . 某同学将刻度尺如图②放置,便刻度尺上的数字对齐数轴上的点 , 发现点对齐刻度尺处,点对齐刻度尺处.
18. 如图①,点 , , 是数轴上从左到右排列的三个点,分别对应的数为 , , . 某同学将刻度尺如图②放置,便刻度尺上的数字对齐数轴上的点 , 发现点对齐刻度尺处,点对齐刻度尺处. (1)、在图①的数轴上,个单位长;(2)、求数轴上点所对应的数为 .19. 如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高时,水柱落点距O点;喷头高时,水柱落点距O点 . 那么喷头高m时,水柱落点距O点 .
(1)、在图①的数轴上,个单位长;(2)、求数轴上点所对应的数为 .19. 如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高时,水柱落点距O点;喷头高时,水柱落点距O点 . 那么喷头高m时,水柱落点距O点 .
三、解答题
-
20. 已知一个三角形的第一条边长为 , 第二条边长为(1)、求第三条边长的取值范围;(用含 , 的式子表示)(2)、若 , 满足 , 第三条边长为整数,求这个三角形周长的最大值21. 数学活动课上,张老师引导同学进行如下探究:
如图①,将长为的铅笔斜靠在垂直于水平桌面的直尺的边沿上,一端固定在桌面上,图②是示意图.
如图③,将铅笔绕端点顺时针旋转,与交于点 , 当旋转至水平位置时,铅笔的中点与点重合.
设 , 点到的距离 .
数学思考: (1)、当 , 求点到的距离;(2)、则分别求出和的长(用含的代数式表示);(3)、求出与的函数关系式,并求出自变量的取值范围22. 已知关于x的一元二次方程 有实数根.(1)、求m的值;(2)、先作 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式.23. 一个不透明的袋中装有4个球,分别标有1、2、3、4四个号码,这些球除号码外都相同.甲同学每次从袋中搅匀后任意摸出一个球后再放回,并计划摸取球10次,现已摸取了8次,取出的结果如表所列:
(1)、当 , 求点到的距离;(2)、则分别求出和的长(用含的代数式表示);(3)、求出与的函数关系式,并求出自变量的取值范围22. 已知关于x的一元二次方程 有实数根.(1)、求m的值;(2)、先作 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式.23. 一个不透明的袋中装有4个球,分别标有1、2、3、4四个号码,这些球除号码外都相同.甲同学每次从袋中搅匀后任意摸出一个球后再放回,并计划摸取球10次,现已摸取了8次,取出的结果如表所列:次数
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
第9次
第10次
号码
2
2
4
4
2
1
4
1
若每次取球时,且取出的号码即为得分,请回答下列问题:
(1)、乙同学说:“甲同学前8次摸球都没有得3分,因此第9次摸球一定得3分.”请分析乙的说法是否正确,说明理由.(2)、请求出第1次至第8次得分的平均数.(3)、甲同学依计划继续从袋中再取球2次,这两次取球得分之和为a,若发生“这10次得分的平均数不小于2.2,且不大于2.4”的情况,①a的取值范围是:;
②请通过列表法或树状图计算发生这种情况的概率.
24. 随着 技术的发展,人们对各类 产品的使用充满期待.某公司计划在某地区销售第一款 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第 ( 为正整数)个销售周期每台的销售价格为 元, 与 之间满足如图所示的一次函数关系.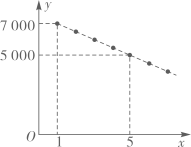 (1)、求 与 之间的关系式;(2)、设该产品在第 个销售周期的销售数量为 (万台), 与 的关系可用 来描述。根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?25. 为弘扬民族传统体育文化,某校将传统游戏“滚铁环”列入了校运动会的比赛项目.滚铁环器材由铁环和推杆组成.小明对滚铁环的启动阶段进行了研究,如图,滚铁环时,铁环⊙O与水平地面相切于点C,推杆AB与铅垂线AD的夹角为∠BAD,点O,A,B,C,D在同一平面内.当推杆AB与铁环⊙O相切于点B时,手上的力量通过切点B传递到铁环上,会有较好的启动效果.
(1)、求 与 之间的关系式;(2)、设该产品在第 个销售周期的销售数量为 (万台), 与 的关系可用 来描述。根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?25. 为弘扬民族传统体育文化,某校将传统游戏“滚铁环”列入了校运动会的比赛项目.滚铁环器材由铁环和推杆组成.小明对滚铁环的启动阶段进行了研究,如图,滚铁环时,铁环⊙O与水平地面相切于点C,推杆AB与铅垂线AD的夹角为∠BAD,点O,A,B,C,D在同一平面内.当推杆AB与铁环⊙O相切于点B时,手上的力量通过切点B传递到铁环上,会有较好的启动效果.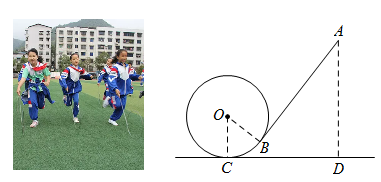 (1)、求证:∠BOC+∠BAD=90°.(2)、实践中发现,切点B只有在铁环上一定区域内时,才能保证铁环平稳启动.图中点B是该区域内最低位置,此时点A距地面的距离AD最小,测得 . 已知铁环⊙O的半径为25cm,推杆AB的长为75cm,求此时AD的长.26. 已知一次函数 的图象与反比例函数 的图象交于点 ,与 轴交于点 ,若 ,且 .
(1)、求证:∠BOC+∠BAD=90°.(2)、实践中发现,切点B只有在铁环上一定区域内时,才能保证铁环平稳启动.图中点B是该区域内最低位置,此时点A距地面的距离AD最小,测得 . 已知铁环⊙O的半径为25cm,推杆AB的长为75cm,求此时AD的长.26. 已知一次函数 的图象与反比例函数 的图象交于点 ,与 轴交于点 ,若 ,且 . (1)、求反比例函数与一次函数的表达式;(2)、若点 为x轴上一点, 是等腰三角形,求点 的坐标.
(1)、求反比例函数与一次函数的表达式;(2)、若点 为x轴上一点, 是等腰三角形,求点 的坐标.