2022-2023学年沪科版数学八年级下册第20章数据的初步分析基础过关单元卷

试卷更新日期：2023-06-20 类型：单元试卷

进入出卷网下载

一、单选题（每题4分，共40分）

1. 将40个数据，分为4组，其中第1、2组的频数分别是6、9，第3组的频率是0.3，则第4组的频率是（）

A、0.25 B、0.35 C、0.4 D、0.325

查看试题解析
2. 对频数分布直方图的下列认识，错误的是（）

A、每小组条形图的横宽等于这组的组距 B、每小组条形图的纵高等于这组的频数 C、每小组条形图的面积等于这组的频率 D、所有小组条形图的个数等于数据分组整理的组数

查看试题解析
3. 某学习小组9名学生参加“生活中的数学知识竞赛”，他们的得分情况如下表

人数（人）

1

3

4

1

分数（分）

80

85

90

95

那么这9名学生所得分数的众数和中位数分别是（）

A、90，90 B、90，85 C、90，87.5 D、85，85

查看试题解析
4. 如图是某班全体学生参加体能测试成绩的频数分布直方图（统计中采用“上限不在内”的原则，如成绩为45分统计在45≤x＜50小组，而不在40≤x＜45小组），根据图形提供的信息，下列说法中错误的是（）

A、该班学生人数为45人 B、分数在45≤x＜50小组的学生人数占全班人数的20% C、小组40≤x＜45的组中值为42.5 D、该班学生体能测试成绩的中位数落在50≤x＜55这一组

查看试题解析
5. 下列说法正确的是（）

A、九年级某班的英语测试平均成绩是98.5分，说明每个同学的得分都是98.5分 B、数据4，4，5，5，0的中位数和众数都是5 C、要了解一批日光灯的使用寿命，应采用全面调查 D、若甲、乙两组数据中各有20个数据，两组数据的平均数相等，方差 $S_{甲}^{2}$ =1.25， $S_{乙}^{2}$ =0.96，则说明乙组数数据比甲组数据稳定

查看试题解析
6. 在八年级数学运算比赛中，A班荣获团体总分第一名．A班参赛选手比赛成绩的方差计算公式为：S²= $\frac{1}{6}$ [(x₁-38)²+(x₂-38)²+……+(x₆-38)²]，下列说法错误的是（）

A、A班一共派出了6名选手 B、A班参赛选手的平均成绩为38分 C、A班选手比赛成绩的中位数为38 D、A班选手比赛成绩的团体总分为228分

查看试题解析
7. 为弘扬中华传统文化，某乡镇举行了一场“诗词背诵”比赛，赛后整理所有参赛选手的成绩 $x$ （单位：分）如表，则m为（）
分数 $x /$ 分
人数 $/$ 名
百分比
$60 \leq x < 70$
30
15%
$70 \leq x < 80$
m
45%
$80 \leq x < 90$
60
n
$90 \leq x < 100$
20
10%

A、45 B、90 C、40 D、50

查看试题解析
8. 某校抽取九年级两个班共80名同学进行体育模拟测试，将测试成绩绘制成如下统计图（满分60分，成绩为整数），若成绩超过45分为合格，则该两个班体育模拟测试成绩合格率为（）

A、72% B、75% C、80% D、85%

查看试题解析
9. 初三（9）班拍合照时，最后一排10位同学的身高（单位：cm）分别为x₁ ， x₂ ， …x₁₀ ，当他们站到一排高度相等的桌子上，头顶离地高度（单位：cm）分别为y₁ ， y₂ ， …y₁₀.对比两组数据，下列统计量中不发生变化的是（）.

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
10. 某组数据的方差计算公式为 $S^{2} = \frac{2 {(2 - \bar{x})}^{2} + 3 {(3 - \bar{x})}^{2} + 2 {(5 - \bar{x})}^{2}}{n}$ ，由公式提供的信息如下：①样本容量为3；②样本中位数为3；③样本众数为3；④样本平均数为 $\frac{10}{3}$ ；其说法正确的有（）

A、①②④ B、②④ C、②③ D、③④

查看试题解析

二、填空题（每空5分，共25分）

11. 某校对1000名学生的身高进行了测量，身高在 $1.58 \sim 1.60$ （单位：m）这一小组的频率为0.26，则该组的人数为．

查看试题解析
12. 一组数据的最大值与最小值差为14，组距为3时，可分为组．

查看试题解析
13. 对某班最近一次数学测试成绩 $($ 得分取整数 $)$ 进行统计分析，将所有成绩由低到高分成五组，并绘制成如图所示的频数分布直方图，根据直方图提供的信息，在这次测试中，成绩为A等 $(80$ 分以上，不含80分 $)$ 的百分率为 $% ． ($ 精确到 $1 %)$

查看试题解析
14. 在样本容量为200的频数直方图中，共有3个小长方形，若第一个长方形对应的频率为10%，若中间一个小长方形的高与其余两个小长方形高的和之比是2：3，则中间一组的频率为.

查看试题解析
15. 数据 $x_{1} ， x_{2} ， x_{3} ， x_{4}$ 的平均数是4，方差是3，则数据 $x_{1} + 1 ， x_{2} + 1 ， x_{3} + 1 ， x_{4} + 1$ 的平均数和方差分别是，．

查看试题解析

三、解答题（共7题，共85分）

16. 为了解某中学八年级250名学生的数学成绩，从中抽取了50名学生的数学成绩进行分析，得到下表：
分数
60分以下
60.5～70.5分
70.5分～80.5分
80.5分～90.5分
90.5分～100.5分
合计
频数
3
6
b
17
15
50
频率
a
0.12
0.18
0.34
0.3
1

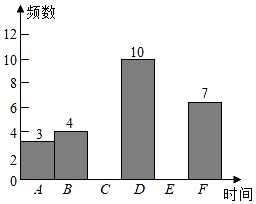
(1)、在这次抽样分析的过程中，样本是；

(2)、表中的数据a= ， b=；

(3)、估计该校八年级这次考试的数学平均成绩约为分；

(4)、在这次考试中该校八年级数学成绩在90.5～100.5范围内的人数为人．

查看试题解析
17. 某学校为了解共青团员志愿服务情况，调查小组根据平台数据进行了抽样问卷调查，过程如下：

(1)、从九年级随机抽取40名共青团员，将其志愿服务时间按如下方式分组：A：0～5小时；B：5～10小时；C：10～15小时；D：15～20小时；E：20～25小时；F：25～30小时．（注：每组含最小值，不含最大值）得到这40名志愿者服务时间如下：BDEACEDBFCDDDBECDEEFAFFADCDBDFCFDECEEECE
并将上述数据整理在频数分布表中，请你补充其中的数据．

志愿服务时间

A

B

C

D

E

F

频数

3

4

10

9

7

(2)、根据上面的频数分布表，小明绘制了频数分布直方图，请将空缺的部分补充完整；

(3)、分析数据：
①观察以上图表，写出一个结论；

②校团委计划组织志愿服务时间不足10小时的团员参加义务劳动，根据上述信息估计九年级200名团员中参加此次义务劳动的人数约为 ▲ 人．

查看试题解析
18. 初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初二学生的参与情况，绘制成如图所示的频数分布直方图和扇形统计图（均不完整），请根据图中所给信息解答下列问题：

(1)、在这次评价中，一共抽查了名学生；

(2)、在扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数为度；

(3)、请将频数分布直方图补充完整；

(4)、如果全市有6000名初二学生，那么在试卷评讲课中，“独立思考”的初二学生约有多少人？

查看试题解析
19. 某县八年级有3000名学生参加“爱我中华知识竞赛”活动．为了了解本次知识竞赛的成绩分布情况，从中随机抽取了部分学生的得分进行统计．请你根据不完整的表格，解答下列问题：
（1）补全频数分布表；
（2）随机抽取的样本容量为多少；
（3）若将得分转化为等级，规定50≤x＜60评为“D”，60≤x＜70评为“C”，70≤x＜90评为“B”，90≤x＜100评为“A”．估计这3000名学生中，有多少学生得分等级为A？
成绩 x 分
频数
频率
50≤x＜60
10
　　
60≤x＜70
16
0.08
70≤x＜80
　　
0.2
80≤x＜90
62
0.31
90≤x＜100
72
0.36

查看试题解析
20. 如图，是甲、乙两名射击运动员一次训练中10次射击环数折线统计图，请判断甲、乙两名射击运动员中谁的成绩的方差小，并计算其方差.

查看试题解析
21. 2022年5月30日是第六个全国科技工作者日，主题为“创新争先，自立自强”．为了庆祝第六个全国科技工作者日，学校举办科技知识竞赛活动，竞赛内容分“航天技术”，“生物技术”，“能源技术”，“其它技术领域”四个项目，下表是小亮和小明的各项成绩：（百分制）

航天技术
生物技术
能源技术
其它技术领域
小亮
85
90
95
90
小明
100
90
80
90
若“航天技术”，“生物技术”，“能源技术”，“其它技术领域”四个项目按 $4 ： 3 ： 2 ： 1$ 确定综合成绩，则小亮和小明谁的综合成绩高？请通过计算说明理由．

查看试题解析
22. 在某段公路上，最高限速65km/h.交警部门设置了雷达探测器监测汽车的行驶速度，以下是交警部门某天一段时间内记录的驶过该处的30辆车的行驶速度（单位：km/h）；
55      49      61       47       49         54      49      57      59      58

50      51      48       49       80         58      48      54      70      71

62      45      56       64       78         52      60      55      49      75

请按组距为10进行分组，列出频数分布表，画出频数分布直方图，并分析有几辆车超速.

查看试题解析

分数 $x /$ 分	人数 $/$ 名	百分比
$60 \leq x < 70$	30	15%
$70 \leq x < 80$	m	45%
$80 \leq x < 90$	60	n
$90 \leq x < 100$	20	10%

分数	60分以下	60.5～70.5分	70.5分～80.5分	80.5分～90.5分	90.5分～100.5分	合计
频数	3	6	b	17	15	50
频率	a	0.12	0.18	0.34	0.3	1

成绩 x 分	频数	频率
50≤x＜60	10
60≤x＜70	16	0.08
70≤x＜80		0.2
80≤x＜90	62	0.31
90≤x＜100	72	0.36

	航天技术	生物技术	能源技术	其它技术领域
小亮	85	90	95	90
小明	100	90	80	90

人数（人）	1	3	4	1
分数（分）	80	85	90	95

志愿服务时间	A	B	C	D	E	F
频数	3	4		10	9	7