2022-2023学年沪科版数学八年级下册第19章四边形基础过关单元卷
试卷更新日期:2023-06-20 类型:单元试卷
一、单选题(每题4分,共40分)
-
1. 在平行四边形中, , 则的度数为( )
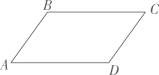 A、 B、 C、 D、2. 如图,四边形的对角线交于点 , 下列不能判定其为平行四边形的是( )
A、 B、 C、 D、2. 如图,四边形的对角线交于点 , 下列不能判定其为平行四边形的是( )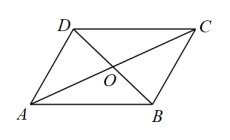 A、 B、 C、 D、3. 如图,在▱中, , 若 , 则的度数是( )
A、 B、 C、 D、3. 如图,在▱中, , 若 , 则的度数是( ) A、 B、 C、 D、4. 如图,点是的对角线上一点,连接 , , 设的面积为 , 的面积为 , 则与的大小关系( )
A、 B、 C、 D、4. 如图,点是的对角线上一点,连接 , , 设的面积为 , 的面积为 , 则与的大小关系( )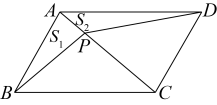 A、 B、 C、 D、无法确定5. 下列命题中,错误的是( )A、两组对边分别相等的四边形是平行四边形 B、有一个角是直角的平行四边形是矩形 C、对角线互相垂直的四边形是菱形 D、有一组邻边相等的矩形是正方形6. 如图,在平面直角坐标系中,菱形 , O为坐标原点,点C在x轴上,A的坐标为 , 则顶点B的坐标是( )
A、 B、 C、 D、无法确定5. 下列命题中,错误的是( )A、两组对边分别相等的四边形是平行四边形 B、有一个角是直角的平行四边形是矩形 C、对角线互相垂直的四边形是菱形 D、有一组邻边相等的矩形是正方形6. 如图,在平面直角坐标系中,菱形 , O为坐标原点,点C在x轴上,A的坐标为 , 则顶点B的坐标是( )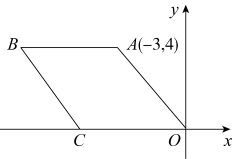 A、 B、 C、 D、7. 用边长相等的两种正多边形地砖铺设地面,要求图形间既无缝隙又不重叠(平面镶嵌),下面选项中的两种正多边形不可以用来平面镶嵌的是( )A、正三角形、正四边形 B、正三角形、正六边形 C、正四边形、正六边形 D、正四边形、正八边形8. 如图,在中,对角线与交于点O, , E为中点,若的周长为32,的周长比的周长多4,则的长为( )
A、 B、 C、 D、7. 用边长相等的两种正多边形地砖铺设地面,要求图形间既无缝隙又不重叠(平面镶嵌),下面选项中的两种正多边形不可以用来平面镶嵌的是( )A、正三角形、正四边形 B、正三角形、正六边形 C、正四边形、正六边形 D、正四边形、正八边形8. 如图,在中,对角线与交于点O, , E为中点,若的周长为32,的周长比的周长多4,则的长为( )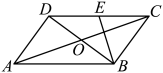 A、3 B、5 C、4 D、9. 如图,四边形中,R、P分别是上的点,E、F分别是的中点,当点P在上从C向D移动而点R不动时,那么下列结论成立的是( )
A、3 B、5 C、4 D、9. 如图,四边形中,R、P分别是上的点,E、F分别是的中点,当点P在上从C向D移动而点R不动时,那么下列结论成立的是( ) A、线段的长逐渐增大 B、线段的长逐渐减小 C、线段的长不变 D、线段的长与点P的位置有关10. 如图,在中, , 且 , , 点D是斜边上的一个动点,过点D分别作于点M,于点N,连接 , 则线段的最小值为( )
A、线段的长逐渐增大 B、线段的长逐渐减小 C、线段的长不变 D、线段的长与点P的位置有关10. 如图,在中, , 且 , , 点D是斜边上的一个动点,过点D分别作于点M,于点N,连接 , 则线段的最小值为( ) A、5 B、3.6 C、2.4 D、4.8
A、5 B、3.6 C、2.4 D、4.8二、填空题(每空5分,共20分)
-
11. 若一个多边形的外角和比这个多边形的内角和小540°,则这个多边形的边数为.12. 如图,在 □ ABCD中,EF∥AD,HN∥AB,则图中的平行四边形共有个。
 13. 如图,在四边形ABCD中,P、Q、M、N分别是AD、BC、BD、AC的中点,当四边形ABCD满足时(填写一个条件),PQ⊥MN.
13. 如图,在四边形ABCD中,P、Q、M、N分别是AD、BC、BD、AC的中点,当四边形ABCD满足时(填写一个条件),PQ⊥MN. 14. 在正方形中, , 点P为对角线上一点,且 , 当点E在边上,时,的长为.
14. 在正方形中, , 点P为对角线上一点,且 , 当点E在边上,时,的长为.三、解答题(共5题,共40分)
-
15. 如图,中,平分 , 平分 , 求证:四边形是平行四边形.
 16. 求图(1)(2)中x的值.
16. 求图(1)(2)中x的值. 17. 如图,在中,过对角线的交点 , 且与边分别相交于点 , , 求四边形的周长.
17. 如图,在中,过对角线的交点 , 且与边分别相交于点 , , 求四边形的周长.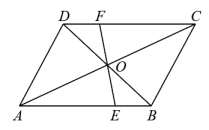 18. 已知:如在△ABC中,AD是∠BAC的平分线,DE∥AC,DF∥AB.
18. 已知:如在△ABC中,AD是∠BAC的平分线,DE∥AC,DF∥AB.求证:四边形AEDF是菱形.
 19. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上, EF⊥AB,OG∥EF.求证:四边形OEFG是矩形
19. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上, EF⊥AB,OG∥EF.求证:四边形OEFG是矩形
四、综合题(共4题,共50分)
-
20. 如图,已知E、F分别是的边、上的点,且 .
 (1)、求证:四边形是平行四边形;(2)、在中,若 , , , 求边上的高 .21. 如图,菱形的对角线相交于点O , 过点A作于点E , 延长到点F , 使 , 连接 .
(1)、求证:四边形是平行四边形;(2)、在中,若 , , , 求边上的高 .21. 如图,菱形的对角线相交于点O , 过点A作于点E , 延长到点F , 使 , 连接 . (1)、求证:四边形AEFD是矩形;(2)、连接 , 若 , . 求的长.22. 如图,在矩形ABCD中,cm,cm,点P从点D出发向点A运动,运动到A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P , Q的速度都是1cm/s.连接PQ , AQ , CP . 设点P , Q运动的时间为ts.
(1)、求证:四边形AEFD是矩形;(2)、连接 , 若 , . 求的长.22. 如图,在矩形ABCD中,cm,cm,点P从点D出发向点A运动,运动到A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P , Q的速度都是1cm/s.连接PQ , AQ , CP . 设点P , Q运动的时间为ts.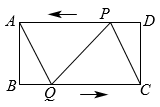 (1)、当t为何值时,四边形ABQP是矩形;(2)、当t为何值时,四边形AQCP是菱形;(3)、分别求出(2)中菱形AQCP的周长和面积.23. 如图:和均为直线AB同侧的等边三角形,点P在内.
(1)、当t为何值时,四边形ABQP是矩形;(2)、当t为何值时,四边形AQCP是菱形;(3)、分别求出(2)中菱形AQCP的周长和面积.23. 如图:和均为直线AB同侧的等边三角形,点P在内. (1)、求证:四边形PEDC为平行四边形;(2)、当点P同时满足条件:①和②时,猜想四边形PEDC是什么特殊的四边形,并说明理由;(3)、若中, , 求四边形PEDC的面积.
(1)、求证:四边形PEDC为平行四边形;(2)、当点P同时满足条件:①和②时,猜想四边形PEDC是什么特殊的四边形,并说明理由;(3)、若中, , 求四边形PEDC的面积.