云南省2023年中考数学试卷
试卷更新日期:2023-06-20 类型:中考真卷
一、单选题
-
1. 中国是最早使用正负数表示具有相反意义的量的国家.若向东走60米记作米,则向西走80米可记作( )A、米 B、0米 C、80米 D、140米2. 云南省矿产资源极为丰富,被誉为“有色金属王国”.锂资源方面,滇中地区被中国科学院地球化学研究所探明拥有氧化锂资源达340000吨.340000用科学记数法可以表示为( )A、 B、 C、 D、3. 如图,直线与直线都相交.若 , 则( )
 A、 B、 C、 D、4. 某班同学用几个几何体组合成一个装饰品美化校园.其中一个几何体的三视图(其中主视图也称正视图,左视图也称侧视图)如图所示,这个几何体是( )
A、 B、 C、 D、4. 某班同学用几个几何体组合成一个装饰品美化校园.其中一个几何体的三视图(其中主视图也称正视图,左视图也称侧视图)如图所示,这个几何体是( ) A、球 B、圆柱 C、长方体 D、圆锥5. 下列计算正确的是( )A、 B、 C、 D、6. 为了解某班学生2023年5月27日参加体育锻炼的情况,从该班学生中随机抽取5名同学进行调查.经统计,他们这天的体育锻炼时间(单位:分钟)分别为65,60,75,60,80.这组数据的众数为( )A、65 B、60 C、75 D、807. 中华文明,源远流长:中华汉字,寓意深广.下列四个选项中,是轴对称图形的为( )A、
A、球 B、圆柱 C、长方体 D、圆锥5. 下列计算正确的是( )A、 B、 C、 D、6. 为了解某班学生2023年5月27日参加体育锻炼的情况,从该班学生中随机抽取5名同学进行调查.经统计,他们这天的体育锻炼时间(单位:分钟)分别为65,60,75,60,80.这组数据的众数为( )A、65 B、60 C、75 D、807. 中华文明,源远流长:中华汉字,寓意深广.下列四个选项中,是轴对称图形的为( )A、 B、
B、 C、
C、 D、
D、 8. 若点是反比例函数图象上一点,则常数的值为( )A、3 B、 C、 D、9. 按一定规律排列的单项式: , 第个单项式是( )A、 B、 C、 D、10. 如图,两点被池塘隔开,三点不共线.设的中点分别为 . 若米,则( )
8. 若点是反比例函数图象上一点,则常数的值为( )A、3 B、 C、 D、9. 按一定规律排列的单项式: , 第个单项式是( )A、 B、 C、 D、10. 如图,两点被池塘隔开,三点不共线.设的中点分别为 . 若米,则( ) A、4米 B、6米 C、8米 D、10米11. 阅读,正如一束阳光.孩子们无论在哪儿,都可以感受到阳光的照耀,都可以通过阅读触及更广阔的世界.某区教育体育局向全区中小学生推出“童心读书会”的分享活动.甲、乙两同学分别从距离活动地点800米和400米的两地同时出发,参加分享活动.甲同学的速度是乙同学的速度的1.2倍,乙同学比甲同学提前4分钟到达活动地点.若设乙同学的速度是米/分,则下列方程正确的是( )A、 B、 C、 D、12. 如图,是的直径,是上一点.若 , 则( )
A、4米 B、6米 C、8米 D、10米11. 阅读,正如一束阳光.孩子们无论在哪儿,都可以感受到阳光的照耀,都可以通过阅读触及更广阔的世界.某区教育体育局向全区中小学生推出“童心读书会”的分享活动.甲、乙两同学分别从距离活动地点800米和400米的两地同时出发,参加分享活动.甲同学的速度是乙同学的速度的1.2倍,乙同学比甲同学提前4分钟到达活动地点.若设乙同学的速度是米/分,则下列方程正确的是( )A、 B、 C、 D、12. 如图,是的直径,是上一点.若 , 则( )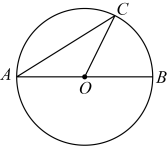 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 函数的自变量的取值范围是 .14. 五边形的内角和是度.15. 分解因式: = .16. 数学活动课上,某同学制作了一顶圆锥形纸帽.若圆锥的底面圆的半径为1分米,母线长为4分米,则该圆锥的高为分米.
三、解答题
-
17. 计算: .18. 如图,是的中点, . 求证: .
 19.
19.调查主题
某公司员工的旅游需求
调查人员
某中学数学兴趣小组
调查方法
抽样调查
背景介绍
某公司计划组织员工前往5个国家全域旅游示范区(以下简称示范区)中的1个自费旅游,这5个示范区为:
A.保山市腾冲市; B.昆明市石林彝族自治县; C.红河哈尼族彝族自治州弥物市; D.大理白族自治州大理市; E.丽江市古城区.
某中学数学兴趣小组针对该公司员工的意向目的地开展抽样调查,并为该公司出具了调查报告(注:每位被抽样调查的员工选择且只选择1个意向前往的示范区).
报告内容


请阅读以上材料,解决下列问题(说明:以上仅展示部分报告内容).
(1)、求本次被抽样调查的员工人数;(2)、该公司总的员工数量为900人,请你估计该公司意向前往保山市腾冲市的员工人数.20. 甲、乙两名同学准备参加种植蔬菜的劳动实践活动,各自随机选择种植辣椒、种植茄子、种植西红柿三种中的一种.记种植辣椒为 , 种植茄子为 , 种植西红柿为 , 假设这两名同学选择种植哪种蔬菜不受任何因素影响,且每一种被选到的可能性相等.记甲同学的选择为 , 乙同学的选择为 .(1)、请用列表法或画树状图法中的一种方法,求所有可能出现的结果总数;(2)、求甲、乙两名同学选择种植同一种蔬菜的概率 .21. 蓝天白云下,青山绿水间,支一顶帐篷,邀亲朋好友,听蝉鸣,闻清风,话家常,好不惬意.某景区为响应文化和旅游部《关于推动露营旅游休闲健康有序发展的指导意见》精神,需要购买两种型号的帐篷.若购买种型号帐篷2顶和种型号帐篷4顶,则需5200元;若购买种型号帐篷3顶和种型号帐篷1顶,则需2800元.(1)、求每顶种型号帐篷和每顶种型号帐篷的价格;(2)、若该景区需要购买两种型号的帐篷共20顶(两种型号的帐篷均需购买),购买种型号帐篷数量不超过购买种型号帐篷数量的 , 为使购买帐篷的总费用最低,应购买种型号帐篷和种型号帐篷各多少顶?购买帐篷的总费用最低为多少元?22. 如图,平行四边形中,分别是的平分线,且分别在边上, . (1)、求证:四边形是菱形;(2)、若 , 的面积等于 , 求平行线与间的距离.23. 如图,是的直径,是上异于的点.外的点在射线上,直线与垂直,垂足为 , 且 . 设的面积为的面积为 .
(1)、求证:四边形是菱形;(2)、若 , 的面积等于 , 求平行线与间的距离.23. 如图,是的直径,是上异于的点.外的点在射线上,直线与垂直,垂足为 , 且 . 设的面积为的面积为 . (1)、判断直线与的位置关系,并证明你的结论;(2)、若 , 求常数的值.24. 数和形是数学研究客观物体的两个方面,数(代数)侧重研究物体数量方面,具有精确性、形(几何)侧重研究物体形的方面,具有直观性.数和形相互联系,可用数来反映空间形式,也可用形来说明数量关系.数形结合就是把两者结合起来考虑问题,充分利用代数、几何各自的优势,数形互化,共同解决问题.
(1)、判断直线与的位置关系,并证明你的结论;(2)、若 , 求常数的值.24. 数和形是数学研究客观物体的两个方面,数(代数)侧重研究物体数量方面,具有精确性、形(几何)侧重研究物体形的方面,具有直观性.数和形相互联系,可用数来反映空间形式,也可用形来说明数量关系.数形结合就是把两者结合起来考虑问题,充分利用代数、几何各自的优势,数形互化,共同解决问题.同学们,请你结合所学的数学解决下列问题.
在平面直角坐标系中,若点的横坐标、纵坐标都为整数,则称这样的点为整点.设函数(实数为常数)的图象为图象 .
(1)、求证:无论取什么实数,图象与轴总有公共点;(2)、是否存在整数 , 使图象与轴的公共点中有整点?若存在,求所有整数的值;若不存在,请说明理由.