四川省宜宾市2023年中考数学试卷

试卷更新日期：2023-06-20 类型：中考真卷

进入出卷网下载

一、单选题

1. 2的相反数是（）

A、2 B、－2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列计算正确的是（　　）

A、 $4 a - 2 a = 2$ B、 $2 a b + 3 b a = 5 a b$ C、 $a + a^{2} = a^{3}$ D、 $5 x^{2} y - 3 x y^{2} = 2 x y$

查看试题解析
3. 下列图案中，既是轴对称图形，又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
4. 为积极践行节能减排的发展理念，宜宾大力推进“电动宜宾”工程，2022年城区已建成充电基础设施接口超过8500个．将8500用科学记数法表示为（　　）

A、 $0.85 \times 1 0^{4}$ B、 $85 \times 1 0^{2}$ C、 $8.5 \times 1 0^{3}$ D、 $8.5 \times 1 0^{4}$

查看试题解析
5. 如图， $A B ∥ C D$ ，且 $∠ A = 40 °$ ， $∠ D = 24 °$ ，则 $∠ E$ 等于（　　）

A、 $40 °$ B、 $32 °$ C、 $24 °$ D、 $16 °$

查看试题解析
6. “今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何”是《孙子算经》卷中著名数学问题．意思是：鸡兔同笼，从上面数，有35个头；从下面数，有94条腿．问鸡兔各有多少只？若设鸡有 $x$ 只，兔有 $y$ 只，则所列方程组正确的是（　　）

A、 ${\begin{array}{l} x + y = 35 \\ 4 x + 2 y = 94 \end{array}$ B、 ${\begin{array}{l} x + y = 35 \\ 2 x + 4 y = 94 \end{array}$ C、 ${\begin{array}{l} x + y = 94 \\ 4 x + 2 y = 35 \end{array}$ D、 ${\begin{array}{l} x + y = 94 \\ 2 x + 4 y = 35 \end{array}$

查看试题解析
7. 如图，已知点 $A 、 B 、 C$ 在 $⊙ O$ 上， $C$ 为 $\overset{⌢}{A B}$ 的中点．若 $∠ B A C = 35 °$ ，则 $∠ A O B$ 等于（　　）

A、 $140 °$ B、 $120 °$ C、 $110 °$ D、 $70 °$

查看试题解析
8. 分式方程 $\frac{x - 2}{x - 3} = \frac{2}{x - 3}$ 的解为（　　）

A、2 B、3 C、4 D、5

查看试题解析
9. 《梦溪笔谈》是我国古代科技著作，其中它记录了计算圆弧长度的“会圆术”．如图， $\overset{⌢}{A B}$ 是以点O为圆心、 $O A$ 为半径的圆弧，N是 $A B$ 的中点， $M N ⊥ A B$ ． “会圆术”给出 $\overset{⌢}{A B}$ 的弧长 $l$ 的近似值计算公式： $l = A B + \frac{M N^{2}}{O A}$ ．当 $O A = 4$ ， $∠ A O B = 60 °$ 时，则 $l$ 的值为（　　）

A、 $11 - 2 \sqrt{3}$ B、 $11 - 4 \sqrt{3}$ C、 $8 - 2 \sqrt{3}$ D、 $8 - 4 \sqrt{3}$

查看试题解析
10. 如图，边长为6的正方形 $A B C D$ 中，M为对角线 $B D$ 上的一点，连接 $A M$ 并延长交 $C D$ 于点P．若 $P M = P C$ ，则 $A M$ 的长为（　　）

A、 $3 (\sqrt{3} - 1)$ B、 $3 (3 \sqrt{3} - 2)$ C、 $6 (\sqrt{3} - 1)$ D、 $6 (3 \sqrt{3} - 2)$

查看试题解析
11. 如图，在平面直角坐标系 $x O y$ 中，点A、B分别在y，x轴上， $B C ⊥ x$ 轴．点M、N分别在线段 $B C$ 、 $A C$ 上， $B M = C M$ ， $N C = 2 A N$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过M、N两点，P为x正半轴上一点，且 $O P ： B P = 1 ： 4$ ， $△ A P N$ 的面积为3，则k的值为（　　）

A、 $\frac{45}{4}$ B、 $\frac{45}{8}$ C、 $\frac{144}{25}$ D、 $\frac{72}{25}$

查看试题解析
12. 如图， $△ A B C$ 和 $△ A D E$ 是以点 $A$ 为直角顶点的等腰直角三角形，把 $△ A D E$ 以 $A$ 为中心顺时针旋转，点 $M$ 为射线 $B D$ 、 $C E$ 的交点．若 $A B = \sqrt{3}$ ， $A D = 1$ ．以下结论：
① $B D = C E$ ；② $B D ⊥ C E$ ；

③当点 $E$ 在 $B A$ 的延长线上时， $M C = \frac{3 - \sqrt{3}}{2}$ ；

④在旋转过程中，当线段 $M B$ 最短时， $△ M B C$ 的面积为 $\frac{1}{2}$ ．

其中正确结论有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 在“庆五四·展风采”的演讲比赛中，7位同学参加决赛，演讲成绩依次为：77，80，79，77，80，79，80．这组数据的中位数是．

查看试题解析
14. 分解因式：x³﹣6x²+9x= .

查看试题解析
15. 若关于x的方程 $x^{2} - 2 (m + 1) x + m + 4 = 0$ 两根的倒数和为1，则m的值为．

查看试题解析
16. 若关于x的不等式组 ${\begin{array}{l} 2 x + 1 > x + a ① \\ \frac{x}{2} + 1 \geq \frac{5}{2} x - 9 ② \end{array}$ 所有整数解的和为 $14$ ，则整数 $a$ 的值为．

查看试题解析
17. 如图， $M$ 是正方形 $A B C D$ 边 $C D$ 的中点， $P$ 是正方形内一点，连接 $B P$ ，线段 $B P$ 以 $B$ 为中心逆时针旋转 $90 °$ 得到线段 $B Q$ ，连接 $M Q$ ．若 $A B = 4$ ， $M P = 1$ ，则 $M Q$ 的最小值为．

查看试题解析
18. 如图，抛物线 $y = a x^{2} + b x + c$ 经过点 $A (- 3 ， 0)$ ，顶点为 $M (- 1 ， m)$ ，且抛物线与 $y$ 轴的交点B在 $(0 ， - 2)$ 和 $(0 ， - 3)$ 之间（不含端点），则下列结论：

①当 $- 3 \leq x \leq 1$ 时， $y \leq 1$ ；

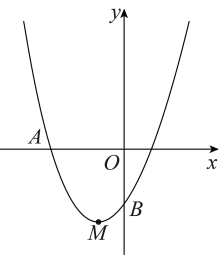
②当 $△ A B M$ 的面积为 $\frac{3 \sqrt{3}}{2}$ 时， $a = \frac{\sqrt{3}}{2}$ ；

③当 $△ A B M$ 为直角三角形时，在 $△ A O B$ 内存在唯一点P，使得 $P A + P O + P B$ 的值最小，最小值的平方为 $18 + 9 \sqrt{3}$ ．

其中正确的结论是．（填写所有正确结论的序号）

查看试题解析

三、解答题

19. 计算

(1)、计算： $2 t a n 45 ° {(- \frac{1}{2})}^{0} + | \sqrt{3} - 1 |$ ．

(2)、化简： $(\frac{1}{x - 2} - \frac{1}{x + 2}) ÷ \frac{x}{x^{2} - 4}$ ．

查看试题解析
20. 已知：如图， $A B ∥ D E$ ， $A B = D E$ ， $A F = D C$ ．求证： $∠ B = ∠ E$ ．

查看试题解析

21. 某校举办“我劳动，我快乐，我光荣”活动．为了解该校九年级学生周末在家的劳动情况，随机调查了九年级1班的所有学生在家劳动时间（单位：小时），并进行了统计和整理绘制如图所示的不完整统计图．根据图表信息回答以下问题：

类别	劳动时间 $x$
A	$0 \leq x < 1$
B	$1 \leq x < 2$
C	$2 \leq x < 3$
D	$3 \leq x < 4$
E	$4 \leq x$

(1)、九年级1班的学生共有人，补全条形统计图；

(2)、若九年级学生共有800人，请估计周末在家劳动时间在3小时及以上的学生人数；

(3)、已知E类学生中恰好有2名女生3名男生，现从中抽取两名学生做劳动交流，请用列表或画树状图的方法，求所抽的两名学生恰好是一男一女的概率．

查看试题解析

22. 渝昆高速铁路的建成，将会显著提升宜宾的交通地位．渝昆高速铁路宜宾临港长江公铁两用大桥（如图 $1$ ），桥面采用国内首创的公铁平层设计．为测量左桥墩底到桥面的距离 $C D$ ，如图 $2$ ．在桥面上点 $A$ 处，测得 $A$ 到左桥墩 $D$ 的距离 $A D = 200$ 米，左桥墩所在塔顶 $B$ 的仰角 $∠ B A D = 45 °$ ，左桥墩底 $C$ 的俯角 $∠ C A D = 15 °$ ，求 $C D$ 的长度．（结果精确到 $1$ 米．参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
23. 如图，在平面直角坐标系 $x O y$ 中，等腰直角三角形 $A B C$ 的直角顶点 $C (3 ， 0)$ ，顶点A、 $B (6 ， m)$ 恰好落在反比例函数 $y = \frac{k}{x}$ 第一象限的图象上．

(1)、分别求反比例函数的表达式和直线 $A B$ 所对应的一次函数的表达式；

(2)、在x轴上是否存在一点P，使 $△ A B P$ 周长的值最小．若存在，求出最小值；若不存在，请说明理由．

查看试题解析
24. 如图，以 $A B$ 为直径的 $⊙ O$ 上有两点 $E$ 、 $F$ ， $\overset{⌢}{B E} = \overset{⌢}{E F}$ ，过点 $E$ 作直线 $C D ⊥ A F$ 交 $A F$ 的延长线于点 $D$ ，交 $A B$ 的延长线于点 $C$ ，过 $C$ 作 $C M$ 平分 $∠ A C D$ 交 $A E$ 于点 $M$ ，交 $B E$ 于点 $N$ ．

(1)、求证： $C D$ 是 $⊙ O$ 的切线；

(2)、求证： $E M = E N$ ；

(3)、如果 $N$ 是 $C M$ 的中点，且 $A B = 9 \sqrt{5}$ ，求 $E N$ 的长．

查看试题解析
25. 如图，抛物线 $y = a x^{2} + b x + c$ 与x轴交于点 $A (- 4 ， 0)$ 、 $B (2 ， 0)$ ，且经过点 $C (- 2 ， 6)$ ．

(1)、求抛物线的表达式；

(2)、在x轴上方的抛物线上任取一点N，射线 $A N$ 、 $B N$ 分别与抛物线的对称轴交于点P、Q，点Q关于x轴的对称点为 $Q^{'}$ ，求 $△ A P Q^{'}$ 的面积；

(3)、点M是y轴上一动点，当 $∠ A M C$ 最大时，求M的坐标．

查看试题解析