四川省遂宁市2023年中考数学试卷

试卷更新日期：2023-06-20 类型：中考真卷

进入出卷网下载

一、单选题

1. 已知算式 $5$ □ $(- 5)$ 的值为 $0$ ，则“□”内应填入的运算符号为（）

A、＋ B、－ C、× D、÷

查看试题解析
2. 下列运算正确的是（）

A、 $(- a)^{2} = - a^{2}$ B、 $3 a^{2} - a^{2} = 3$ C、 $a^{3} \cdot a = a^{4}$ D、 $(a - 1)^{2} = a^{2} - 1$

查看试题解析
3. 纳米是表示微小距离的单位，1纳米 $= 0.000001$ 毫米，而1毫米相当于我们通常使用的刻度尺上的一小格，可想而知1纳米是多么的小．中科院物理所研究员解思深领导的研究组研制出世界上最细的碳纳米管——直径 $0.5$ 纳米． $0.5$ 纳米相当于 $0.0000005$ 毫米，数据 $0.0000005$ 用科学记数法可以表示为（）

A、 $0.5 \times 1 0^{- 6}$ B、 $0.5 \times 1 0^{- 7}$ C、 $5 \times 1 0^{- 6}$ D、 $5 \times 1 0^{- 7}$

查看试题解析
4. 生活中一些常见的物体可以抽象成立体图形，以下立体图形中三视图形状相同的可能是（）

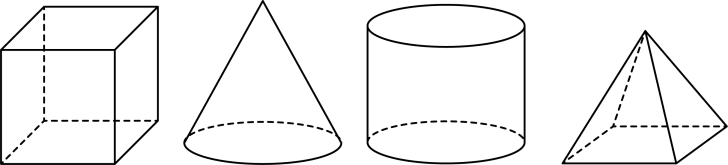A、正方体 B、圆锥 C、圆柱 D、四棱锥

查看试题解析
5. 《九章算术》是我国古代数学的经典书，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等；交易其一，金轻十三两.问金、银一枚各重几何？”意思是甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等.两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计）.问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，则可列方程组为（）

A、 ${\begin{array}{l} 11 x = 9 y \\ (10 y + x) - (8 x + y) = 13 \end{array}$ B、 ${\begin{array}{l} 9 x = 11 y \\ (8 x + y) - (10 y + x) = 13 \end{array}$ C、 ${\begin{array}{l} 9 x = 11 y \\ (10 y + x) - (8 x + y) = 13 \end{array}$ D、 ${\begin{array}{l} 11 x = 9 y \\ (8 x + y) - (10 y + x) = 13 \end{array}$

查看试题解析
6. 在方格图中，以格点为顶点的三角形叫做格点三角形．在如图所示的平面直角坐标系中，格点 $△ A B C 、 △ D E F$ 成位似关系，则位似中心的坐标为（）

A、 $(- 1 ， 0)$ B、 $(0 ， 0)$ C、 $(0 ， 1)$ D、 $(1 ， 0)$

查看试题解析
7. 为增强班级凝聚力，吴老师组织开展了一次主题班会．班会上，他设计了一个如图的飞镖靶盘，靶盘由两个同心圆构成，小圆半径为 $10 c m$ ，大圆半径为 $20 c m$ ，每个扇形的圆心角为60度．如果用飞镖击中靶盘每一处是等可能的，那么小全同学任意投掷飞镖1次（击中边界或没有击中靶盘，则重投1次），投中“免一次作业”的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{8}$ C、 $\frac{1}{10}$ D、 $\frac{1}{12}$

查看试题解析
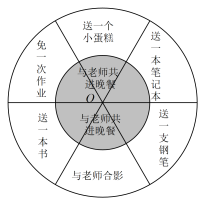8. 若关于x的不等式组 ${\begin{array}{l} 4 (x - 1) > 3 x - 1 \\ 5 x > 3 x + 2 a \end{array}$ 的解集为 $x > 3$ ，则a的取值范围是（）

A、 $a > 3$ B、 $a < 3$ C、 $a \geq 3$ D、 $a \leq 3$

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = 10 ， B C = 6 ， A C = 8$ ，点P为线段 $A B$ 上的动点，以每秒1个单位长度的速度从点A向点B移动，到达点B时停止．过点P作 $P M ⊥ A C$ 于点M、作 $P N ⊥ B C$ 于点N，连接 $M N$ ，线段 $M N$ 的长度y与点P的运动时间t（秒）的函数关系如图所示，则函数图象最低点E的坐标为（）

A、 $(5 ， 5)$ B、 $(6 ， \frac{24}{5})$ C、 $(\frac{32}{5} ， \frac{24}{5})$ D、 $(\frac{32}{5} ， 5)$

查看试题解析
10. 抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，对称轴为直线 $x = - 2$ ．下列说法：① $a b c < 0$ ；② $c - 3 a > 0$ ；③ $4 a^{2} - 2 a b ≥ a t (a t + b)$ （t为全体实数）；④若图象上存在点 $A (x_{1} ， y_{1})$ 和点 $B (x_{2} ， y_{2})$ ，当 $m < x_{1} < x_{2} < m + 3$ 时，满足 $y_{1} = y_{2}$ ，则m的取值范围为 $- 5 < m < - 2$ ．其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若三角形三个内角的比为1：2：3，则这个三角形按角分类是三角形．

查看试题解析
12. 若a、b是一元二次方程 $x^{2} - 3 x + 1 = 0$ 的两个实数根，则代数式 $a + b - a b$ 的值为．

查看试题解析
13. 烷烃是一类由碳、氢元素组成的有机化合物，在生产生活中可作为燃料、润滑剂等原料，也可用于动、植物的养护．通常用碳原子的个数命名为甲烷、乙烷、丙烷、……、癸烷（当碳原子数目超过 $10$ 个时即用汉文数字表示，如十一烷、十二烷……）等，甲烷的化学式为 $C H_{4}$ ，乙烷的化学式为 $C_{2} H_{6}$ ，丙烷的化学式为 $C_{3} H_{8}$ ……，其分子结构模型如图所示，按照此规律，十二烷的化学式为．

查看试题解析
14. 如图， $▱ A B C D$ 中， $B D$ 为对角线，分别以点A、B为圆心，以大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧相交于点M、N，作直线 $M N$ 交 $A D$ 于点E，交 $A B$ 于点F，若 $A D ⊥ B D$ ， $B D = 4$ ， $B C = 8$ ，则 $A E$ 的长为．

查看试题解析
15. 如图，以 $△ A B C$ 的边 $A B$ 、 $A C$ 为腰分别向外作等腰直角 $△ A B E$ 、 $△ A C D$ ，连结 $E D$ 、 $B D$ 、 $E C$ ，过点 $A$ 的直线 $l$ 分别交线段 $D F$ 、 $B C$ 于点 $M$ 、 $N$ ，以下说法：①当 $A B = A C = B C$ 时， $∠ A E D = 30 °$ ；② $E C = B D$ ；③若 $A B = 3$ ， $A C = 4$ ， $B C = 6$ ，则 $D E = 2 \sqrt{3}$ ；④当直线 $l ⊥ B C$ 时，点 $M$ 为线段 $D E$ 的中点．正确的有． (填序号)

查看试题解析

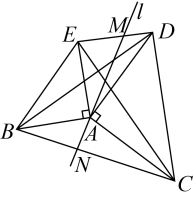
三、解答题

16. 计算： $2 s i n 30 ° - 8 + {(2 - π)}^{0} + {(- 1)}^{2023}$

查看试题解析
17. 先化简，再求值： $\frac{x^{2} - 2 x + 1}{x^{2} - 1} \cdot (1 + \frac{1}{x})$ ，其中 $x = {(\frac{1}{2})}^{- 1}$ ．

查看试题解析
18. 为贯彻落实党的二十大关于深化全民阅读活动的重要部署，教育部印发了《全国青少年学生读书行动实施方案》，于是某中学开展了以“书香润校园，好书伴成长”为主题的系列读书活动．学校为了解学生周末的阅读情况，采用随机抽样的方式获取了若干名学生的周末阅读时间数据，整理后得到下列不完整的图表：
类别
A类
B类
C类
D类
阅读时长t（小时）
$0 \leq t < 1$
$1 \leq t < 2$
$2 \leq t < 3$
$t \geq 3$
频数
8
m
n
4

请根据图表中提供的信息，解答下面的问题：

(1)、此次调查共抽取了名学生， $m =$ ， $n =$ ；

(2)、扇形统计图中，B类所对应的扇形的圆心角是度；

(3)、已知在D类的4名学生中有两名男生和两名女生，若从中随机抽取两人参加阅读分享活动，请用列表或画树状图的方法求出恰好抽到一名男生和一名女生的概率．

查看试题解析
19. 如图，四边形 $A B C D$ 中， $A D ∥ B C$ ，点O为对角线 $B D$ 的中点，过点O的直线l分别与 $A D$ 、 $B C$ 所在的直线相交于点E、F．（点E不与点D重合）

(1)、求证： $△ D O E ≌ △ B O F$ ；

(2)、当直线 $l ⊥ B D$ 时，连接 $B E$ 、 $D F$ ，试判断四边形 $E B F D$ 的形状，并说明理由．

查看试题解析
20. 我们规定：对于任意实数a、b、c、d有 $[a ， b] * [c ， d] = a c - b d$ ，其中等式右边是通常的乘法和减法运算，如： $[3 ， 2] * [5 ， 1] = 3 \times 5 - 2 \times 1 = 13$ ．

(1)、求 $[- 4 ， 3] * [2 ， - 6]$ 的值；

(2)、已知关于x的方程 $[x ， 2 x - 1] * [m x + 1 ， m] = 0$ 有两个实数根，求m的取值范围．

查看试题解析
21. 端午节是我国入选世界非物质文化遗产的传统节日，端午节吃粽子是中华民族的传统习俗．某超市为了满足人们的需求，计划在端午节前购进甲、乙两种粽子进行销售，经了解．每个乙种粽子的进价比每个甲种粽子的进价多2元，用1000元购进甲种粽子的个数与用1200元购进乙种粽子的个数相同．

(1)、甲、乙两种粽子每个的进价分别是多少元？

(2)、该超市计划购进这两种粽子共200个（两种都有），其中甲种粽子的个数不低于乙种粽子个数的2倍，若甲、乙两种粽子的售价分别为12元/个、15元/个，设购进甲种粽子m个，两种粽子全部售完时获得的利润为w元．
①求w与m的函数关系式，并求出m的取值范围；
②超市应如何进货才能获得最大利润，最大利润是多少元？

查看试题解析

22. 某实践探究小组想测得湖边两处的距离，数据勘测组通过勘测，得到了如下记录表：

实践探究活动记录表
活动内容测量湖边A、B两处的距离
成员组长：××× 组员：××××××××××××
测量工具测角仪，皮尺等
测量示意图		说明：因为湖边A、B两处的距离无法直接测量，数据勘测组在湖边找了一处位置C．可测量C处到A、B两处的距离．通过测角仪可测得 $∠ A 、 ∠ B 、 ∠ C$ 的度数．
测量数据	角的度数	$∠ A = 30 °$
		$∠ B = 45 °$
		$∠ C = 105 °$
	边的长度	$B C = 40.0$ 米
		$A C = 56.4$ 米

数据处理组得到上面数据以后做了认真分析．他们发现不需要勘测组的全部数据就可以计算出A、B之间的距离．于是数据处理组写出了以下过程，请补全内容．

(1)、

已知：如图，在 $△ A B C$ 中， $∠ A = 30 ° ， ∠ B = 45 °$ ． ____．（从记录表中再选一个条件填入横线）

求：线段 $A B$ 的长．（为减小结果的误差，若有需要， $\sqrt{2}$ 取 $1.41$ ， $\sqrt{3}$ 取 $1.73$ ， $\sqrt{6}$ 取 $2.45$ 进行计算，最后结果保留整数．）

查看试题解析

23. 如图，一次函数 $y = k_{1} x + b$ 的图像与反比例函数 $y = \frac{k_{2}}{x}$ 的图像交于 $A (- 4 ， 1)$ ， $B (m ， 4)$ 两点．（ $k_{1}$ ， $k_{2}$ ， $b$ 为常数）

(1)、求一次函数和反比例函数的解析式；

(2)、根据图像直接写出不等式 $k_{1} x + b > \frac{k_{2}}{x}$ 的解集；

(3)、 $P$ 为 $y$ 轴上一点，若 $△ P A B$ 的面积为 $3$ ，求 $P$ 点的坐标．

查看试题解析
24. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ， $A B$ 为 $⊙ O$ 的直径， $A D = C D$ ，过点 $D$ 的直线l交 $B A$ 的延长线于点 $M$ ，交 $B C$ 的延长线于点 $N$ ，且 $∠ A D M = ∠ D A C$ ．

(1)、求证： $M N$ 是 $⊙ O$ 的切线；

(2)、求证： $A D^{2} = A B \cdot C N$ ；

(3)、当 $A B = 6$ ， $s i n ∠ D C A = \frac{\sqrt{3}}{3}$ 时，求 $A M$ 的长．

查看试题解析
25. 在平面直角坐标系中， $O$ 为坐标原点，抛物线 $y = \frac{1}{4} x^{2} + b x + c$ 经过点 $O (0$ ， $0)$ ，对称轴过点 $B (2$ ， $0)$ ，直线 $l$ 过点 $C (2 ， - 2)$ ，且垂直于 $y$ 轴．过点 $B$ 的直线 $l_{1}$ 交抛物线于点 $M$ 、 $N$ ，交直线 $l$ 于点 $Q$ ，其中点 $M$ 、Q在抛物线对称轴的左侧．
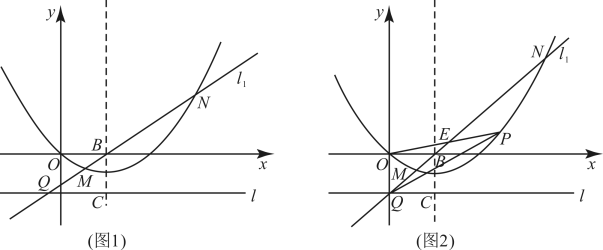(1)求抛物线的解析式；

(1)、如图1，当 $B M ： M Q = 3 ： 5$ 时，求点 $N$ 的坐标；

(2)、如图2，当点 $Q$ 恰好在 $y$ 轴上时， $P$ 为直线 $l_{1}$ 下方的抛物线上一动点，连接 $P Q$ 、 $P O$ ，其中 $P O$ 交 $l_{1}$ 于点 $E$ ，设 $△ O Q E$ 的面积为 $S_{1}$ ， $△ P Q E$ 的面积为 $S_{2}$ ．求 $\frac{S_{2}}{S_{1}}$ 的最大值．

查看试题解析

类别	A类	B类	C类	D类
阅读时长t（小时）	$0 \leq t < 1$	$1 \leq t < 2$	$2 \leq t < 3$	$t \geq 3$
频数	8	m	n	4