江西省2023年中考数学试卷
试卷更新日期:2023-06-20 类型:中考真卷
一、单选题
-
1. 下列各数中,正整数是( )A、 B、 C、 D、2. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若有意义,则的值可以是( )A、 B、 C、 D、4. 计算的结果为( )A、 B、 C、 D、5. 如图,平面镜放置在水平地面上,墙面于点 , 一束光线照射到镜面上,反射光线为 , 点在上,若 , 则的度数为( )
3. 若有意义,则的值可以是( )A、 B、 C、 D、4. 计算的结果为( )A、 B、 C、 D、5. 如图,平面镜放置在水平地面上,墙面于点 , 一束光线照射到镜面上,反射光线为 , 点在上,若 , 则的度数为( ) A、 B、 C、 D、6. 如图,点 , , , 均在直线上,点在直线外,则经过其中任意三个点,最多可画出圆的个数为( )
A、 B、 C、 D、6. 如图,点 , , , 均在直线上,点在直线外,则经过其中任意三个点,最多可画出圆的个数为( )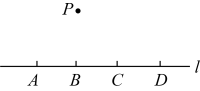 A、3个 B、4个 C、5个 D、6个
A、3个 B、4个 C、5个 D、6个二、填空题
-
7. 单项式的系数为 .8. 我国海洋经济复苏态势强劲.在建和新开工海上风电项目建设规模约1800万千瓦,比上一年同期翻一番,将18000000用科学记数法表示应为 .9. 计算:(a+1)2﹣a2= .10. 将含角的直角三角板和直尺按如图所示的方式放置,已 , 点 , 表示的刻度分别为 , 则线段的长为cm.
 11. 《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度如图,点 , , 在同一水平线上,和均为直角,与相交于点 . 测得 , 则树高m.
11. 《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度如图,点 , , 在同一水平线上,和均为直角,与相交于点 . 测得 , 则树高m.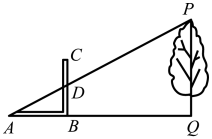 12. 如图,在中, , 将绕点逆时针旋转角()得到 , 连接 , . 当为直角三角形时,旋转角的度数为 .
12. 如图,在中, , 将绕点逆时针旋转角()得到 , 连接 , . 当为直角三角形时,旋转角的度数为 .
三、解答题
-
13.(1)、计算:(2)、如图, , 平分 . 求证: .
 14. 如图是的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
14. 如图是的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).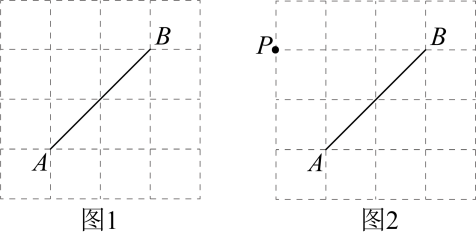 (1)、在图1中作锐角 , 使点C在格点上;(2)、在图2中的线段上作点Q,使最短.15. 化简 . 下面是甲、乙两同学的部分运算过程:
(1)、在图1中作锐角 , 使点C在格点上;(2)、在图2中的线段上作点Q,使最短.15. 化简 . 下面是甲、乙两同学的部分运算过程:
解:原式
……
解:原式
……
 (1)、甲同学解法的依据是 , 乙同学解法的依据是;(填序号)
(1)、甲同学解法的依据是 , 乙同学解法的依据是;(填序号)①等式的基本性质;②分式的基本性质;③乘法分配律;④乘法交换律.
(2)、请选择一种解法,写出完整的解答过程.16. 为了弘扬雷锋精神,某校组织“学雷锋,争做新时代好少年”的宣传活动根据活动要求,每班需要2名宣传员某班班主任决定从甲、乙、丙、丁4名同学中随机选取2名同学作为宣传员.(1)、“甲、乙同学都被选为宣传员”是事件:(填“必然”、“不可能”或“随机”)(2)、请用画树状图法或列表法,求甲、丁同学都被选为宣传员的概率.17. 如图,已知直线与反比例函数的图象交于点 , 与y轴交于点B,过点B作x轴的平行线交反比例函数的图象于点C. (1)、求直线和反比例函数图象的表达式;(2)、求的面积.18. 今年植树节,某班同学共同种植一批树苗,如果每人种3棵,则剩余20棵;如果每人种4棵,则还缺25棵.(1)、求该班的学生人数;(2)、这批树苗只有甲、乙两种,其中甲树苗每棵30元,乙树苗每棵40元.购买这批树苗的总费用没有超过5400元,请问至少购买了甲树苗多少棵?19. 如图1是某红色文化主题公园内的雕塑,将其抽象成加如图2所示的示意图,已知点 , , , 均在同一直线上, , 测得 . (结果保小数点后一位)
(1)、求直线和反比例函数图象的表达式;(2)、求的面积.18. 今年植树节,某班同学共同种植一批树苗,如果每人种3棵,则剩余20棵;如果每人种4棵,则还缺25棵.(1)、求该班的学生人数;(2)、这批树苗只有甲、乙两种,其中甲树苗每棵30元,乙树苗每棵40元.购买这批树苗的总费用没有超过5400元,请问至少购买了甲树苗多少棵?19. 如图1是某红色文化主题公园内的雕塑,将其抽象成加如图2所示的示意图,已知点 , , , 均在同一直线上, , 测得 . (结果保小数点后一位)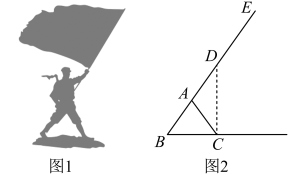 (1)、连接 , 求证:;(2)、求雕塑的高(即点E到直线BC的距离).
(1)、连接 , 求证:;(2)、求雕塑的高(即点E到直线BC的距离).(参考数据:)
20. 如图,在中, , 以为直径的与相交于点D,E为上一点,且 . (1)、求的长;(2)、若 , 求证:为的切线.21. 为了解中学生的视力情况,某区卫健部门决定随机抽取本区部分初、高中学生进行调查,并对他们的视力数据进行整理,得到如下统计表和统计图.
(1)、求的长;(2)、若 , 求证:为的切线.21. 为了解中学生的视力情况,某区卫健部门决定随机抽取本区部分初、高中学生进行调查,并对他们的视力数据进行整理,得到如下统计表和统计图.整理描述
初中学生视力情况统计表
视力
人数
百分比
0.6及以下
8
0.7
16
0.8
28
0.9
34
m
及以上
46
n
合计
200
高中学生视力情况统计图
 (1)、 , ;(2)、被调查的高中学生视力情况的样本容量为;(3)、分析处理:①小胡说:“初中学生的视力水平比高中学生的好.”请你对小胡的说法进行判断,并选择一个能反映总体的统计量说明理由:
(1)、 , ;(2)、被调查的高中学生视力情况的样本容量为;(3)、分析处理:①小胡说:“初中学生的视力水平比高中学生的好.”请你对小胡的说法进行判断,并选择一个能反映总体的统计量说明理由:②约定:视力未达到为视力不良.若该区有26000名初中学生,估计该区有多少名初中学生视力不良?并对视力保护提出一条合理化建议.
22. 课本再现思考
我们知道,菱形的对角线互相垂直.反过来,对角线互相垂直的平行四边形是菱形吗?
可以发现并证明菱形的一个判定定理;
对角线互相垂直的平行四边形是菱形.
(1)、定理证明:为了证明该定理,小明同学画出了图形(如图1),并写出了“已知”和“求证”,请你完成证明过程.已知:在中,对角线 , 垂足为 .
求证:是菱形.
 (2)、知识应用:如图 , 在中,对角线和相交于点 , .
(2)、知识应用:如图 , 在中,对角线和相交于点 , .
①求证:是菱形;
②延长至点 , 连接交于点 , 若 , 求的值.
23. 综合与实践问题提出:某兴趣小组开展综合实践活动:在中, , D为上一点, , 动点P以每秒1个单位的速度从C点出发,在三角形边上沿匀速运动,到达点A时停止,以为边作正方形设点P的运动时间为 , 正方形的面积为S,探究S与t的关系
 (1)、初步感知:如图1,当点P由点C运动到点B时,
(1)、初步感知:如图1,当点P由点C运动到点B时,①当时, .
②S关于t的函数解析式为 .
(2)、当点P由点B运动到点A时,经探究发现S是关于t的二次函数,并绘制成如图2所示的图象请根据图象信息,求S关于t的函数解析式及线段的长.(3)、延伸探究:若存在3个时刻()对应的正方形的面积均相等.①;
②当时,求正方形的面积 .