四川省眉山市2023年中考数学试卷
试卷更新日期:2023-06-20 类型:中考真卷
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 生物学家发现了某种花粉的直径约为毫米,数据用科学记数法表示正确的是( )A、 B、 C、 D、3. 下列运算中,正确的是( )A、 B、 C、 D、4. 如图,中, , 则的度数为( )
 A、 B、 C、 D、5. 已知一组数据为2,3,4,5,6,则该组数据的方差为( )A、2 B、4 C、6 D、106. 关于x的一元二次方程有两个不相等的实数根,则m的取值范围是( )A、 B、 C、 D、7. 已知关于的二元一次方程组的解满足 , 则m的值为( )A、0 B、1 C、2 D、38. 由相同的小正方体搭成的立体图形的部分视图如图所示,则搭成该立体图形的小正方体的最少个数为( )
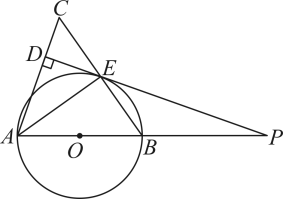
A、 B、 C、 D、5. 已知一组数据为2,3,4,5,6,则该组数据的方差为( )A、2 B、4 C、6 D、106. 关于x的一元二次方程有两个不相等的实数根,则m的取值范围是( )A、 B、 C、 D、7. 已知关于的二元一次方程组的解满足 , 则m的值为( )A、0 B、1 C、2 D、38. 由相同的小正方体搭成的立体图形的部分视图如图所示,则搭成该立体图形的小正方体的最少个数为( )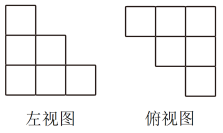 A、6 B、9 C、10 D、149. 关于x的不等式组的整数解仅有4个,则m的取值范围是( )A、 B、 C、 D、10. 如图,切于点B,连接交于点C,交于点D,连接 , 若 , 则的度数为( )
A、6 B、9 C、10 D、149. 关于x的不等式组的整数解仅有4个,则m的取值范围是( )A、 B、 C、 D、10. 如图,切于点B,连接交于点C,交于点D,连接 , 若 , 则的度数为( ) A、 B、 C、 D、11. 如图,二次函数的图象与x轴的一个交点坐标为 , 对称轴为直线 , 下列四个结论:①;②;③;④当时,;其中正确结论的个数为( )
A、 B、 C、 D、11. 如图,二次函数的图象与x轴的一个交点坐标为 , 对称轴为直线 , 下列四个结论:①;②;③;④当时,;其中正确结论的个数为( ) A、1个 B、2个 C、3个 D、4个12. 如图,在正方形中,点E是上一点,延长至点F,使 , 连结 , 交于点K,过点A作 , 垂足为点H,交于点G,连结 . 下列四个结论:①;②;③;④ . 其中正确结论的个数为( )
A、1个 B、2个 C、3个 D、4个12. 如图,在正方形中,点E是上一点,延长至点F,使 , 连结 , 交于点K,过点A作 , 垂足为点H,交于点G,连结 . 下列四个结论:①;②;③;④ . 其中正确结论的个数为( )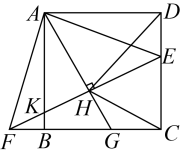 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 分解因式: .14. 已知方程的根为 , 则的值为 .15. 如图,中,是中线,分别以点A,点B为圆心,大于长为半径作弧,两孤交于点M,N.直线交于点E.连接交于点F.过点D作 , 交于点G.若 , 则的长为 .
 16. 关于x的方程的解为非负数,则m的取值范围是 .17. 一渔船在海上A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行12海里到达点B处,测得灯塔C在它的北偏东45°方向,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是海里.
16. 关于x的方程的解为非负数,则m的取值范围是 .17. 一渔船在海上A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行12海里到达点B处,测得灯塔C在它的北偏东45°方向,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是海里.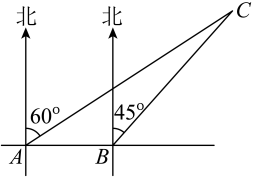 18. 如图,在平面直角坐标系中,点B的坐标为 , 过点B分别作x轴、y轴的垂线,垂足分别为点C、点A,直线与交于点D.与y轴交于点E.动点M在线段上,动点N在直线上,若是以点N为直角顶点的等腰直角三角形,则点M的坐标为
18. 如图,在平面直角坐标系中,点B的坐标为 , 过点B分别作x轴、y轴的垂线,垂足分别为点C、点A,直线与交于点D.与y轴交于点E.动点M在线段上,动点N在直线上,若是以点N为直角顶点的等腰直角三角形,则点M的坐标为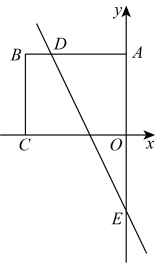
三、解答题
-
19. 计算:20. 先化简: , 再从选择中一个合适的数作为x的值代入求值.21. 某校为落实“双减”工作,推行“五育并举”,计划成立五个兴趣活动小组(每个学生只能参加一个活动小组):A.音乐,B.美术,C.体育,D.阅读,E.人工智能,为了解学生对以上兴趣活动的参与情况,随机抽取了部分学生进行调查统计,并根据统计结果,绘制成了如图所示的两幅不完整的统计图:

根据图中信息,完成下列问题:
(1)、①补全条形统计图(要求在条形图上方注明人数);②扇形统计图中的圆心角的度数为 .
(2)、若该校有3600名学生,估计该校参加E组(人工智能)的学生人数;(3)、该学校从E组中挑选出了表现最好的两名男生和两名女生,计划从这四位同学中随机抽取两人参加市青少年人工智能竞赛,请用画树状图或列表的方法求出恰好抽到一名男生一名女生的概率.22. 如图,中,点E是的中点,连接并延长交的延长线于点F. (1)、求证:;(2)、点G是线段上一点,满足 , 交于点H,若 , 求的长.23. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然正气.”某校为提高学生的阅读品味,现决定购买获得矛盾文学奖的甲、乙两种书共100本,已知购买2本甲种书和1本乙种书共需100元,购买3本甲种书和2本乙种书共需165元.(1)、求甲,乙两种书的单价分别为多少元:(2)、若学校决定购买以上两种书的总费用不超过3200元,那么该校最多可以购买甲种书多少本?24. 如图,在平面直角坐标系中,直线与x轴交于点 , 与y轴交于点 , 与反比例函数在第四象限内的图象交于点 .
(1)、求证:;(2)、点G是线段上一点,满足 , 交于点H,若 , 求的长.23. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然正气.”某校为提高学生的阅读品味,现决定购买获得矛盾文学奖的甲、乙两种书共100本,已知购买2本甲种书和1本乙种书共需100元,购买3本甲种书和2本乙种书共需165元.(1)、求甲,乙两种书的单价分别为多少元:(2)、若学校决定购买以上两种书的总费用不超过3200元,那么该校最多可以购买甲种书多少本?24. 如图,在平面直角坐标系中,直线与x轴交于点 , 与y轴交于点 , 与反比例函数在第四象限内的图象交于点 .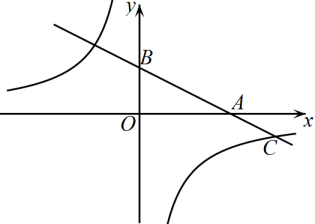 (1)、求反比例函数的表达式:(2)、当时,直接写出x的取值范围;(3)、在双曲线上是否存在点P,使是以点A为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求反比例函数的表达式:(2)、当时,直接写出x的取值范围;(3)、在双曲线上是否存在点P,使是以点A为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.