四川省南充市2023年中考数学试卷
试卷更新日期:2023-06-20 类型:中考真卷
一、单选题
-
1. 如果向东走10m记作 , 那么向西走记作( )A、 B、 C、 D、2. 如图,将沿向右平移得到 , 若 , , 则的长是( )
 A、2 B、 C、3 D、53. 某女鞋专卖店在一周内销售了某种女鞋60双,对这批鞋子尺码及销量进行统计,得到条形统计图(如图).根据图中信息,建议下次进货量最多的女鞋尺码是( )
A、2 B、 C、3 D、53. 某女鞋专卖店在一周内销售了某种女鞋60双,对这批鞋子尺码及销量进行统计,得到条形统计图(如图).根据图中信息,建议下次进货量最多的女鞋尺码是( )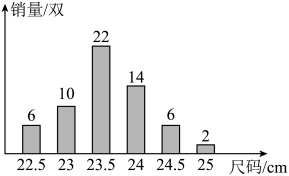 A、22cm B、22.5cm C、23cm D、23.5cm4. 如图,小兵同学从处出发向正东方向走米到达处,再向正北方向走到处,已知 , 则 , 两处相距( )
A、22cm B、22.5cm C、23cm D、23.5cm4. 如图,小兵同学从处出发向正东方向走米到达处,再向正北方向走到处,已知 , 则 , 两处相距( ) A、米 B、米 C、米 D、米5. 《孙子算经》记载:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”(尺、寸是长度单位,1尺=10寸).意思是,现有一根长木,不知道其长短.用一根绳子去度量长木,绳子还剩余4.5尺;将绳子对折再度量长木,长木还剩余1尺.问长木长多少?设长木长为x尺,则可列方程为( )A、 B、 C、 D、6. 如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为 , 同时量得小菲与镜子的水平距离为 , 镜子与旗杆的水平距离为 , 则旗杆高度为( )
A、米 B、米 C、米 D、米5. 《孙子算经》记载:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”(尺、寸是长度单位,1尺=10寸).意思是,现有一根长木,不知道其长短.用一根绳子去度量长木,绳子还剩余4.5尺;将绳子对折再度量长木,长木还剩余1尺.问长木长多少?设长木长为x尺,则可列方程为( )A、 B、 C、 D、6. 如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为 , 同时量得小菲与镜子的水平距离为 , 镜子与旗杆的水平距离为 , 则旗杆高度为( ) A、 B、 C、 D、7. 若点在抛物线()上,则下列各点在抛物线上的是( )A、 B、 C、 D、8. 如图,在中, , 以点A为圆心,适当长为半径画弧,分别交于点M,N,再分别以M,N为圆心,大于的长为半径画弧,两弧在的内部相交于点P,画射线与交于点D, , 垂足为E.则下列结论错误的是( )
A、 B、 C、 D、7. 若点在抛物线()上,则下列各点在抛物线上的是( )A、 B、 C、 D、8. 如图,在中, , 以点A为圆心,适当长为半径画弧,分别交于点M,N,再分别以M,N为圆心,大于的长为半径画弧,两弧在的内部相交于点P,画射线与交于点D, , 垂足为E.则下列结论错误的是( )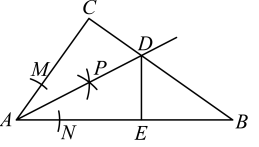 A、 B、 C、 D、9. 关于x,y的方程组的解满足 , 则的值是( )A、1 B、2 C、4 D、810. 抛物线与x轴的一个交点为 , 若 , 则实数的取值范围是( )A、 B、或 C、 D、或
A、 B、 C、 D、9. 关于x,y的方程组的解满足 , 则的值是( )A、1 B、2 C、4 D、810. 抛物线与x轴的一个交点为 , 若 , 则实数的取值范围是( )A、 B、或 C、 D、或二、填空题
-
11. 若分式的值为0,则的值为 .12. 不透明袋中有红、白两种颜色的小球,这些球除颜色外无其他差别.从袋中随机取出一个球是红球的概率为 , 若袋中有4个白球,则袋中红球有个.13. 如图,是的直径,点D,M分别是弦 , 弧的中点, , 则的长是 .
 14. 小伟用撬棍撬动一块大石头,已知阻力和阻力臂分别为1000N和0.6m,当动力臂由1.5m增加到2m时,撬动这块石头可以节省N的力.(杜杆原理:阻力阻力臂动力动力臂)15. 如图,直线(k为常数,)与x,y轴分别交于点A,B,则的值是 .
14. 小伟用撬棍撬动一块大石头,已知阻力和阻力臂分别为1000N和0.6m,当动力臂由1.5m增加到2m时,撬动这块石头可以节省N的力.(杜杆原理:阻力阻力臂动力动力臂)15. 如图,直线(k为常数,)与x,y轴分别交于点A,B,则的值是 . 16. 如图,在等边中,过点C作射线 , 点M,N分别在边 , 上,将沿折叠,使点B落在射线上的点处,连接 , 已知 . 给出下列四个结论:①为定值;②当时,四边形为菱形;③当点N与C重合时,;④当最短时, . 其中正确的结论是(填写序号)
16. 如图,在等边中,过点C作射线 , 点M,N分别在边 , 上,将沿折叠,使点B落在射线上的点处,连接 , 已知 . 给出下列四个结论:①为定值;②当时,四边形为菱形;③当点N与C重合时,;④当最短时, . 其中正确的结论是(填写序号)
三、解答题
-
17. 先化简,再求值: , 其中 .18. 如图,在中,点 , 在对角线上, . 求证:
 (1)、;(2)、 .19. 为培养学生劳动习惯,提升学生劳动技能,某校在五月第二周开展了劳动教育实践周活动.七(1)班提供了四类活动:A.物品整理,B.环境美化,C.植物栽培,D.工具制作.要求每个学生选择其中一项活动参加,该班数学科代表对全班学生参与四类活动情况进行了统计,并绘制成统计图(如图).
(1)、;(2)、 .19. 为培养学生劳动习惯,提升学生劳动技能,某校在五月第二周开展了劳动教育实践周活动.七(1)班提供了四类活动:A.物品整理,B.环境美化,C.植物栽培,D.工具制作.要求每个学生选择其中一项活动参加,该班数学科代表对全班学生参与四类活动情况进行了统计,并绘制成统计图(如图). (1)、已知该班有15人参加A类活动,则参加C类活动有多少人?(2)、该班参加D类活动的学生中有2名女生和2名男生获得一等奖,其中一名女生叫王丽,若从获得一等奖的学生中随机抽取两人参加学校“工具制作”比赛,求刚好抽中王丽和1名男生的概率.20. 已知关于x的一元二次方程(1)、求证:无论m为何值,方程总有实数根;(2)、若 , 是方程的两个实数根,且 , 求m的值.21. 如图,一次函数图象与反比例函数图象交于点 , , 与x轴交于点C,与y轴交于点D.
(1)、已知该班有15人参加A类活动,则参加C类活动有多少人?(2)、该班参加D类活动的学生中有2名女生和2名男生获得一等奖,其中一名女生叫王丽,若从获得一等奖的学生中随机抽取两人参加学校“工具制作”比赛,求刚好抽中王丽和1名男生的概率.20. 已知关于x的一元二次方程(1)、求证:无论m为何值,方程总有实数根;(2)、若 , 是方程的两个实数根,且 , 求m的值.21. 如图,一次函数图象与反比例函数图象交于点 , , 与x轴交于点C,与y轴交于点D. (1)、求反比例函数与一次函数的解析式;(2)、点M在x轴上,若 , 求点M的坐标.22. 如图,与相切于点A,半径 , 与相交于点D,连接 .
(1)、求反比例函数与一次函数的解析式;(2)、点M在x轴上,若 , 求点M的坐标.22. 如图,与相切于点A,半径 , 与相交于点D,连接 .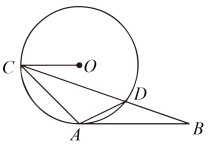 (1)、求证:;(2)、若 , 求的长.23. 某工厂计划从A,B两种产品中选择一种生产并销售,每日产销x件.已知A产品成本价m元/件(m为常数,且 , 售价8元/件,每日最多产销500件,同时每日共支付专利费30元;B产品成本价12元/件,售价20元/件,每日最多产销300件,同时每日支付专利费y元,y(元)与每日产销x(件)满足关系式(1)、若产销A,B两种产品的日利润分别为元,元,请分别写出 , 与x的函数关系式,并写出x的取值范围;(2)、分别求出产销A,B两种产品的最大日利润.(A产品的最大日利润用含m的代数式表示)(3)、为获得最大日利润,该工厂应该选择产销哪种产品?并说明理由.【利润(售价成本)产销数量专利费】24. 如图,正方形中,点在边上,点是的中点,连接 , .
(1)、求证:;(2)、若 , 求的长.23. 某工厂计划从A,B两种产品中选择一种生产并销售,每日产销x件.已知A产品成本价m元/件(m为常数,且 , 售价8元/件,每日最多产销500件,同时每日共支付专利费30元;B产品成本价12元/件,售价20元/件,每日最多产销300件,同时每日支付专利费y元,y(元)与每日产销x(件)满足关系式(1)、若产销A,B两种产品的日利润分别为元,元,请分别写出 , 与x的函数关系式,并写出x的取值范围;(2)、分别求出产销A,B两种产品的最大日利润.(A产品的最大日利润用含m的代数式表示)(3)、为获得最大日利润,该工厂应该选择产销哪种产品?并说明理由.【利润(售价成本)产销数量专利费】24. 如图,正方形中,点在边上,点是的中点,连接 , . (1)、求证:;(2)、将绕点逆时针旋转,使点的对应点落在上,连接 . 当点在边上运动时(点不与 , 重合),判断的形状,并说明理由.(3)、在(2)的条件下,已知 , 当时,求的长.25. 如图1,抛物线()与轴交于 , 两点,与轴交于点 .
(1)、求证:;(2)、将绕点逆时针旋转,使点的对应点落在上,连接 . 当点在边上运动时(点不与 , 重合),判断的形状,并说明理由.(3)、在(2)的条件下,已知 , 当时,求的长.25. 如图1,抛物线()与轴交于 , 两点,与轴交于点 . (1)、求抛物线的解析式;(2)、点P在抛物线上,点Q在x轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;(3)、如图2,抛物线顶点为D,对称轴与x轴交于点E,过点的直线(直线除外)与抛物线交于G,H两点,直线 , 分别交x轴于点M,N.试探究是否为定值,若是,求出该定值;若不是,说明理由.
(1)、求抛物线的解析式;(2)、点P在抛物线上,点Q在x轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;(3)、如图2,抛物线顶点为D,对称轴与x轴交于点E,过点的直线(直线除外)与抛物线交于G,H两点,直线 , 分别交x轴于点M,N.试探究是否为定值,若是,求出该定值;若不是,说明理由.