浙江省台州市2023年中考数学试卷
试卷更新日期:2023-06-20 类型:中考真卷
一、选择题(本题有10小题,每小题4分,共40分。请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
-
1. 下列各数中,最小的是( ).A、2 B、1 C、 D、
-
2. 如图是由5个相同的正方体搭成的立体图形,其主视图是( ).
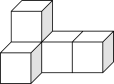 A、
A、 B、
B、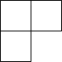 C、
C、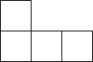 D、
D、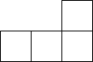
-
3. 下列无理数中,大小在3与4之间的是( ).A、 B、 C、 D、
-
4. 下列运算正确的是( ).A、 B、 C、 D、
-
5. 不等式的解集在数轴上表示为( ).A、
 B、
B、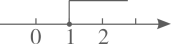 C、
C、 D、
D、
-
6. 如图是中国象棋棋盘的一部分,建立如图所示的平面直角坐标系,已知“車”所在位留的坐标为 , 则“炮”所在位置的坐标为( ).
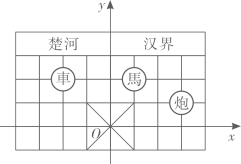 A、 B、 C、 D、
A、 B、 C、 D、 -
7. 以下调查中,适合全面调查的是( ).A、了解全国中学生的视力情况 B、检测“神舟十六号”飞船的零部件 C、检测台州的城市空气质量 D、调查某池塘中现有鱼的数量
-
8. 如图,的圆心O与正方形的中心重合,已知的半径和正方形的边长都为4,则圆上任意一点到正方形边上任意一点距离的最小值为( ).
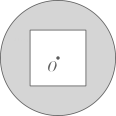 A、 B、2 C、 D、
A、 B、2 C、 D、 -
9. 如图,锐角三角形ABC中, , 点D,E分别在边AB,AC上,连接BE,CD.下列命题中,假命题是( ).
 A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则 -
10. 抛物线与直线交于 , 两点,若 , 则直线一定经过( ).A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限
二、填空题(本题有6小题,每小题5分,共30分)
-
11. 因式分解:.
-
12. 一个不透明的口袋中有5个除颜色外完全相同的小球,其中2个红球,3个白球.随机摸出一个小球,摸出红球的概率是 .
-
13. 用一张等宽的纸条折成如图所示的图案,若 , 则∠2的度数为 .

-
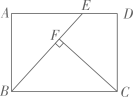
14. 如图,矩形ABCD中, , . 在边AD上取一点E,使 , 过点C作 , 垂足为点F,则BF的长为 .
-
15. 3月12日植树节期间,某校环保小卫士组织植树活动.第一组植树12棵;第二组比第一组多6人,植树36棵;结果两组平均每人植树的棵数相等,则第一组有人.
-
16. 如图,点C,D在线段AB上(点C在点A,D之间),分别以AD,BC为边向同侧作等边三角形ADE与等边三角形CBF,边长分别为a,b.CF与DE交于点H,延长AE,BF交于点G,AG长为c.
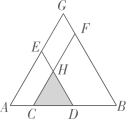 (1)、若四边形EHFG的周长与△CDH的周长相等,则a,b,c之间的等量关系为 .(2)、若四边形EHFG的面积与△CDH的面积相等,则a,b,c之间的等量关系为 .
(1)、若四边形EHFG的周长与△CDH的周长相等,则a,b,c之间的等量关系为 .(2)、若四边形EHFG的面积与△CDH的面积相等,则a,b,c之间的等量关系为 .
三、解答题(本题有8小题,第17~20题毎题8分,笰21题10分,第22,23题每题12分,第24题14分,共80分)
-
17. 计算: .
-
18. 解方程组:
-
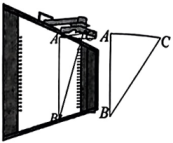
19. 教室里的投影仪投影时,可以把投影光线CA,CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC, . 黑板上投影图像的高度 , CB与AB的夹角 , 求AC的长.(结果精确到1cm.参考数据: , , )
-
20. 科学课上,同学用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度(单位:)的反比例函数,当密度计悬浮在密度为的水中时, .
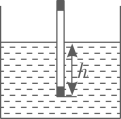 (1)、求h关于的函数解析式.(2)、当密度计悬浮在另一种液体中时, , 求该液体的密度 .
(1)、求h关于的函数解析式.(2)、当密度计悬浮在另一种液体中时, , 求该液体的密度 . -
21. 如图,四边形ABCD中, , , BD为对角线.
 (1)、证明:四边形ABCD是平行四边形.(2)、已知 , 请用无刻度的直尺和圆规作菱形BEDF,顶点E,F分别在边BC,AD上(保留作图痕迹,不要求写作法).
(1)、证明:四边形ABCD是平行四边形.(2)、已知 , 请用无刻度的直尺和圆规作菱形BEDF,顶点E,F分别在边BC,AD上(保留作图痕迹,不要求写作法). -
22. 为了改进几何教学,张老师选择A,B两班进行教学实验研究,在实验班B实施新的教学方法,在控制班A采用原来的教学方法.在实验开始前,进行一次几何能力测试(前测,总分25分),经过一段时间的教学后,再用难度、题型、总分相同的试卷进行测试(后测),得到前测和后测数据并整理成表1和表2.
表1:前测数据
测试分数x
控制班A
28
9
9
3
1
实验班B
25
10
8
2
1
表2:后测数据
测试分数x
控制班A
14
16
12
6
2
实验班B
6
8
11
18
3
(1)、A,B两班的学生人数分别是多少?(2)、请选择一种适当的统计量,分析比较A,B两班的后测数据.(3)、通过分析前测、后测数据,请对张老师的教学实验效果进行评价. -
23. 我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系,用直线上点的位置刻画圆上点的位置,如图,AB是的直径,直线l是的切线,B为切点.P,Q是圆上两点(不与点A重合,且在直径AB的同侧),分别作射线AP,AQ交直线l于点C,点D.
 (1)、如图1,当 , 长为时,求BC的长.(2)、如图2,当 , 时,求的值.(3)、如图3,当 , 时,连接BP,PQ,直接写出的值.
(1)、如图1,当 , 长为时,求BC的长.(2)、如图2,当 , 时,求的值.(3)、如图3,当 , 时,连接BP,PQ,直接写出的值. -
24. 【问题背景】
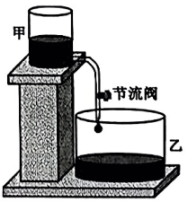
“刻漏”是我国古代的一种利用水流计时的工具.综合实践小组准备用甲、乙两个透明的竖直放置的容器和一根带节流阀(控制水的流速大小)的软管制作简易计时装置.
【实验操作】
综合实践小组设计了如下的实验:先在甲容器里加满水,此时水面高度为30cm,开始放水后每隔10min观察一次甲容器中的水面高度,获得的数据如下表:
流水时间t/min
0
10
20
30
40
水面高度h/cm(观察值)
30
29
28.1
27
25.8
任务1 分别计算表中每隔10min水面高度观察值的变化量.
【建立模型】
小组讨论发现:“ , ”是初始状态下的准确数据,水面高度值的变化不均匀,但可以用一次函数近似地刻画水面高度h与流水时间t的关系.
任务2 利用时,;时,这两组数据求水面高度h与流水时间t的函数解析式.
【反思优化】
经检验,发现有两组表中观察值不满足任务2中求出的函数解析式,存在偏差.小组决定优化函数解析式,减少偏差.通过查阅资料后知道:t为表中数据时,根据解析式求出所对应的函数值,计算这些函数值与对应h的观察值之差的平方和 , 记为w;w越小,偏差越小.
任务3 ⑴计算任务2得到的函数解析式的w值.
⑵请确定经过的一次函数解析式,使得w的值最小.
【设计刻度】
得到优化的函数解析式后,综合实践小组决定在甲容器外壁设计刻度,通过刻度直接读取时间.
任务4 请你简要写出时间刻度的设计方案.
