2022~2023学年安徽省合肥市八年级下册期末数学考试仿真卷(2)
试卷更新日期:2023-06-19 类型:期末考试
一、单选题(每题4分,共40分)
-
1. 下列根式中是最简二次根式的是( )A、 B、 C、 D、2. 一个n边形的每个外角都是40°,则这个n边形的内角和是( )A、360° B、1260° C、1620° D、2160°3. 以下列数组为边长,能构成直角三角形的是( )A、2,3,4 B、1, , C、1, , D、0.2,0.5,0.64. 用配方法解方程 ,配方正确的是( )A、 B、 C、 D、5. 下列结论中,矩形具有而平行四边形不一定具有的性质是( )A、对边平行且相等 B、对角线互相平分 C、任意两个邻角互补 D、对角线相等6. 某厂一月份生产某机器100台,计划二、三月份共生产280台.设二、三月份每月的平均增长率为x , 根据题意列出的方程是( )A、 B、 C、 D、7. 下列说法正确的是( )A、调查中央电视台《开学第一课》的收视率,应采用全面调查的方式 B、数据3,5,4,1,2的中位数是4 C、“清明时节雨纷纷”是必然事件 D、甲、乙两名射击运动员10次射击成绩(单位:环)的平均数相等,方差分别为 , , 则甲的成绩比乙的稳定8. 如图,在平行四边形ABCD中,于点E,于点F,若 , 则( )
 A、 B、 C、 D、9. 如图,在中, , 是的中点,作 , 垂足在线段上,连接 , , 则下列结论:①;②;③;④ . 其中结论正确的序号是( )
A、 B、 C、 D、9. 如图,在中, , 是的中点,作 , 垂足在线段上,连接 , , 则下列结论:①;②;③;④ . 其中结论正确的序号是( )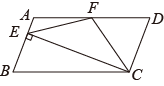 A、①② B、②③④ C、①②④ D、①②③④10. 如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=100°,则∠C的度数为( )
A、①② B、②③④ C、①②④ D、①②③④10. 如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=100°,则∠C的度数为( ) A、40° B、41° C、42° D、43°
A、40° B、41° C、42° D、43°二、填空题(每空5分,共20分)
-
11. 已知 , 则的值为.12. 一幅图案在某个顶点处由三个边长相等的正多边形镶嵌而成.其中的两个正六边形和正十二边形,则第三个多边形的边数是.13. 已知 , ( )是一元二次方程 的两个实数根,则代数式 的值为 .14. 如图,在 中, , 、 是边 上的点,连结 、 ,先将边 沿 折叠,使点 的对称点 落在边 上;再将边 沿 折叠,使点 的对称点 落在 的延长线上.若 , ,则线段 的长为 .

三、计算题(共2题,共16分)
-
15. 计算16. 解方程:3x2=6x﹣2.
四、作图题(共8分)
-
17. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,的三个顶点都是格点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
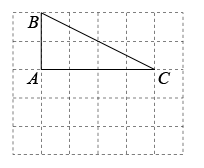 (1)、在图中画出平行四边形 , 为格点;(2)、在边上画一点 , 使得;(3)、找到格点 , 画出直线 , 使得平分平行四边形的面积.
(1)、在图中画出平行四边形 , 为格点;(2)、在边上画一点 , 使得;(3)、找到格点 , 画出直线 , 使得平分平行四边形的面积.五、解答题(共3题,共30分)
-
18. 一条东西走向的公路上有A , B两个站点(视为直线上的两点)相距 , C , D为两村庄(视为两个点),于点A , 于点B(如图),已知 , , 现在要在公路上建一个土特产储藏仓库P , 使得C , D两村庄到储藏仓库P的直线距离相等,请求出储藏仓库P到A站点的距离(精确到)
 19. 已知关于的方程有两个不相等的实数根.(1)、求的取值范围;(2)、设方程的两个根分别为 , , 若 , 求的值及方程的根.20.
19. 已知关于的方程有两个不相等的实数根.(1)、求的取值范围;(2)、设方程的两个根分别为 , , 若 , 求的值及方程的根.20.如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.
(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长.

六、综合题(共3题,共36分)
-
21. 公安交警部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定.某头盔经销商统计了某品牌头盔4月份到6月份的销量,该品牌头盔4月份销售150个,6月份销售216个,且从4月份到6月份销售量的月增长率相同.(1)、求该品牌头盔销售量的月增长率;(2)、若此种头盔的进价为30元/个,测算在市场中,当售价为40元/个时,月销售量为600个,若在此基础上售价每上涨1元/个,则月销售量将减少10个,为使月销售利润达到10000元,而且尽可能让顾客得到实惠,则该品牌头盔的实际售价应定为多少元/个?22. 设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x≤85为B级,60≤x≤75为C级,0<x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
 (1)、在这次调查中,一共抽取了名学生;(2)、扇形统计图中,α=%,C级对应的圆心角为度;(3)、请你利用你所学的统计知识,估计本次抽取所有学生的综合评定成绩的平均分.23. 在平行四边形中,的平分线交边于点E,交的延长线于点F.
(1)、在这次调查中,一共抽取了名学生;(2)、扇形统计图中,α=%,C级对应的圆心角为度;(3)、请你利用你所学的统计知识,估计本次抽取所有学生的综合评定成绩的平均分.23. 在平行四边形中,的平分线交边于点E,交的延长线于点F. (1)、如图1,求证:;(2)、如图2, , , 连接、 , 当时,求证:;(3)、在(2)的条件下,当 , 时,求线段的长.
(1)、如图1,求证:;(2)、如图2, , , 连接、 , 当时,求证:;(3)、在(2)的条件下,当 , 时,求线段的长.
-