四川省资阳市安岳县2023年中考二模数学试卷
试卷更新日期:2023-06-19 类型:中考模拟
一、单选题
-
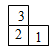
1. 2的绝对值是( )A、2 B、-2 C、 D、2. 如图是由6个相同的小立方体堆成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,则这个几何体的主视图是( )
 A、
A、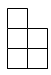 B、
B、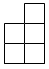 C、
C、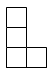 D、
D、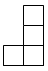 3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,直线 , 若 , , 则的度数为( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,直线 , 若 , , 则的度数为( ) A、 B、 C、 D、5. 小星同学在对数据12,23,36,2■,12,12进行统计时,发现第四个数的个位数字被墨水污染而无法看清,则下列统计量与被污染数字无关的是( )A、平均数 B、中位数 C、众数 D、方差6. 如图,以正方形的边向外作正五边形 , 则的度数为( )
A、 B、 C、 D、5. 小星同学在对数据12,23,36,2■,12,12进行统计时,发现第四个数的个位数字被墨水污染而无法看清,则下列统计量与被污染数字无关的是( )A、平均数 B、中位数 C、众数 D、方差6. 如图,以正方形的边向外作正五边形 , 则的度数为( )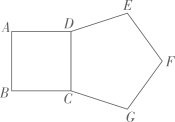 A、172° B、162° C、152° D、150°7. 如图,在中,∠C=90°,分别以A、B为圆心,大于长为半径画弧,两弧相交于D、E两点,直线交于点F.若 , , 则的长为( )
A、172° B、162° C、152° D、150°7. 如图,在中,∠C=90°,分别以A、B为圆心,大于长为半径画弧,两弧相交于D、E两点,直线交于点F.若 , , 则的长为( ) A、4 B、3.5 C、3 D、2.58. 如图,在矩形中, , 平分交于点E,以B为圆心,长为半径画弧,交于点F.若点E为的中点,则图中阴影部分的面积为( )
A、4 B、3.5 C、3 D、2.58. 如图,在矩形中, , 平分交于点E,以B为圆心,长为半径画弧,交于点F.若点E为的中点,则图中阴影部分的面积为( )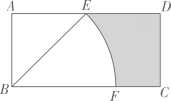 A、 B、 C、 D、9. 天干地支纪年法源于中国,是上古文明的产物,又称节气历或中国阳历,有十天干与十二地支,如表:
A、 B、 C、 D、9. 天干地支纪年法源于中国,是上古文明的产物,又称节气历或中国阳历,有十天干与十二地支,如表:天干
甲
乙
丙
丁
戊
己
庚
辛
壬
癸
4
5
6
7
8
9
0
1
2
3
地支
子
丑
寅
卯
辰
已
午
未
申
酉
戌
亥
4
5
6
7
8
9
10
11
12
1
2
3
算法如下:先用年份的尾数查出天干,再用年份除以12的余数查出地支.如2014年,尾数4为甲,2014除以12余数为10,10为午,那么2014年就是甲午年.则2023年是( )
A、甲卯年 B、甲寅年 C、癸卯年 D、癸寅年10. 已知抛物线 , 当时,y随x的增大而减小,则a的取值范围为( )A、 B、 C、 D、二、填空题
-
11. 使代数式 有意义的x的取值范围是 .12. 一个袋中装有m个红球,n个白球,6个黄球,每个球除颜色外其余都相同,任意摸出一个球,摸到黄球的概率为 , 则的值为 .13. 2023年3月5日,国务院总理李克强在政府工作报告中指出,我国国内生产总值增加到1210000亿元,五年年均增长 , 在高基数基础上实现了中高速增长、迈向高质量发展.请将数“亿”用科学记数法表示为 .14. 如图,、是的两条直径,切于点 , 交的延长线于点 . 若 , 则的度数为 .
 15. “二十四节气”是华夏祖先历经千百年的实践创造出来的宝贵遗产,它与白昼时长密切相关,是反映天气气候和物候变化、掌握农事季节的工具.如图所示是一年中部分节气所对应的白昼时长示意图,则立春、清明、寒露、小寒这四个节气中,白昼时长最短的节气是 .
15. “二十四节气”是华夏祖先历经千百年的实践创造出来的宝贵遗产,它与白昼时长密切相关,是反映天气气候和物候变化、掌握农事季节的工具.如图所示是一年中部分节气所对应的白昼时长示意图,则立春、清明、寒露、小寒这四个节气中,白昼时长最短的节气是 . 16. 如图,正方形的边长为15,点E为延长线上一点,且 , , 连接交于点G.若G是的中点,则的长为 .
16. 如图,正方形的边长为15,点E为延长线上一点,且 , , 连接交于点G.若G是的中点,则的长为 .
三、解答题
-
17. 先化简,再求值: , 其中 .18. 2023年全国两会于3月4日至13日在北京举行,这是一次具有里程碑意义的大会,必将对中国和世界产生深远影响.某校积极组织学生学习两会精神,并组织了知识竞赛(竞赛结果分为A,B,C,D四个等级),且将竞赛结果绘制成如图所示的两幅不完整的统计图.请解答下列问题:
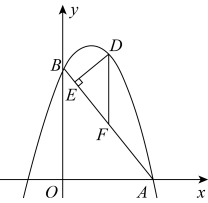
 (1)、求该校参加知识竞赛的学生人数,并补全条形统计图;(2)、求扇形统计图中C等级所对应扇形圆心角的度数;(3)、现准备从A等级的4人(两男两女)中随机抽取两名同学参加两会宣讲,请用画树状图或列表法求出恰好抽到1名男生和1名女生的概率.19. “端午临仲夏,时清日复长.”临近端午节,一网红门店接到一份粽子订单,立即决定由甲、乙两组加工完成.已知甲、乙两组加工一天共生产350袋粽子,甲组加工2天比乙组加工1天多生产250袋粽子.(1)、求甲、乙两组平均每天各能加工多少袋粽子?(2)、已知这份粽子订单为1700袋,若甲、乙两组共用10天加工完成,则甲组至少加工多少天?20. 如图,在中, , D是的中点,E是的中点,交的延长线于点F,连接 .
(1)、求该校参加知识竞赛的学生人数,并补全条形统计图;(2)、求扇形统计图中C等级所对应扇形圆心角的度数;(3)、现准备从A等级的4人(两男两女)中随机抽取两名同学参加两会宣讲,请用画树状图或列表法求出恰好抽到1名男生和1名女生的概率.19. “端午临仲夏,时清日复长.”临近端午节,一网红门店接到一份粽子订单,立即决定由甲、乙两组加工完成.已知甲、乙两组加工一天共生产350袋粽子,甲组加工2天比乙组加工1天多生产250袋粽子.(1)、求甲、乙两组平均每天各能加工多少袋粽子?(2)、已知这份粽子订单为1700袋,若甲、乙两组共用10天加工完成,则甲组至少加工多少天?20. 如图,在中, , D是的中点,E是的中点,交的延长线于点F,连接 .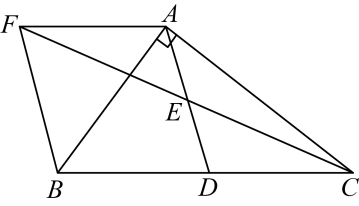 (1)、求证:四边形是菱形;(2)、若 , 求菱形的面积.21. 如图,已知直线与双曲线交于 , 两点.
(1)、求证:四边形是菱形;(2)、若 , 求菱形的面积.21. 如图,已知直线与双曲线交于 , 两点. (1)、求直线的解析式;(2)、将直线向下平移4个单位后与双曲线交于两点,与y轴交于点,求的面积.22. 如图,我国某海域上有、两个小岛,在的正东方向.有一艘渔船在点处捕鱼,在岛测得渔船在东北方向上,在岛测得渔船在北偏西的方向上,且测得、两处的距离为海里.
(1)、求直线的解析式;(2)、将直线向下平移4个单位后与双曲线交于两点,与y轴交于点,求的面积.22. 如图,我国某海域上有、两个小岛,在的正东方向.有一艘渔船在点处捕鱼,在岛测得渔船在东北方向上,在岛测得渔船在北偏西的方向上,且测得、两处的距离为海里.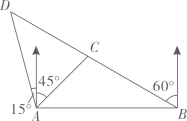 (1)、求、两处的距离;(2)、突然,渔船发生故障,而滞留处等待救援.此时,在处巡逻的救援船立即以每小时海里的速度沿方向前往处,测得在小岛的北偏西方向上距岛海里处.求救援船到达处所用的时间(结果保留根号).
(1)、求、两处的距离;(2)、突然,渔船发生故障,而滞留处等待救援.此时,在处巡逻的救援船立即以每小时海里的速度沿方向前往处,测得在小岛的北偏西方向上距岛海里处.求救援船到达处所用的时间(结果保留根号).