四川省宜宾市2023年中考三模数学试卷
试卷更新日期:2023-06-19 类型:中考模拟
一、单选题
-
1. 8的相反数是( )A、-8 B、8 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 2022年十三届全国人大五次会议审议通过的政府工作报告中提出,今年城镇新增就业目标为11000000人以上.数据11000000用科学记数法表示应为( )A、 B、 C、 D、4. 为庆祝神舟十四号发射成功,学校开展航天知识竞赛活动.经过几轮筛选,本班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛,经过统计,四名同学成绩的平均数(单位:分)及方差(单位:分2)如表所示:
甲
乙
丙
丁
平均数
96
98
95
98
方差
2
0.4
0.4
1.6
如果要选一名成绩好且状态稳定的同学参赛,那么应该选择( )
A、甲 B、乙 C、丙 D、丁5. 如图,直线 , , 则( ) A、 B、 C、 D、6. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能够组合得到如图2所示的四边形.若 , , , 则的值为( )
A、 B、 C、 D、6. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能够组合得到如图2所示的四边形.若 , , , 则的值为( )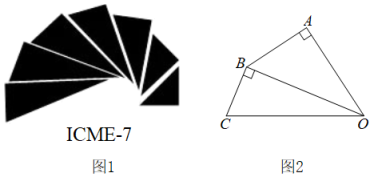 A、 B、 C、 D、17. 点 , , , 在反比例函数 图象上,则 , , , 中最小的是( )A、 B、 C、 D、8. 《九章算术》中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到900里远的城市,所需时间比规定时间多1天;若改为快马派送,则所需时间比规定时间少3天,已知快马的速度是慢马速度的2倍,求规定时间,设规定时间为天,则可列出正确的方程为( )A、 B、 C、 D、9. 设a,b是方程的两个实数根,则的值为( )A、2024 B、2021 C、2023 D、202210. 如图,在平面直角坐标系中, 的顶点 在第一象限,点 , 的坐标分别为 、 , , ,直线 交 轴于点 ,若 与 关于点 成中心对称,则点 的坐标为( )
A、 B、 C、 D、17. 点 , , , 在反比例函数 图象上,则 , , , 中最小的是( )A、 B、 C、 D、8. 《九章算术》中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到900里远的城市,所需时间比规定时间多1天;若改为快马派送,则所需时间比规定时间少3天,已知快马的速度是慢马速度的2倍,求规定时间,设规定时间为天,则可列出正确的方程为( )A、 B、 C、 D、9. 设a,b是方程的两个实数根,则的值为( )A、2024 B、2021 C、2023 D、202210. 如图,在平面直角坐标系中, 的顶点 在第一象限,点 , 的坐标分别为 、 , , ,直线 交 轴于点 ,若 与 关于点 成中心对称,则点 的坐标为( )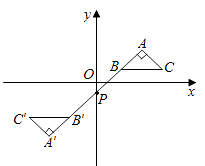 A、 B、 C、 D、11. 二次函数 的图象与一次函数 在同一平面直角坐标系中的图象可能是( )A、
A、 B、 C、 D、11. 二次函数 的图象与一次函数 在同一平面直角坐标系中的图象可能是( )A、 B、
B、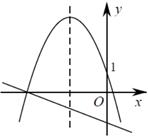 C、
C、 D、
D、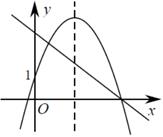 12. 如图,平面直角坐标系中,在直线和轴之间由小到大依次画出若干个等腰直角三角形(图中所示的阴影部分),其中一条直角边在轴上,另一条直角边与轴垂直,则第100个等腰直角三角形的面积是( )
12. 如图,平面直角坐标系中,在直线和轴之间由小到大依次画出若干个等腰直角三角形(图中所示的阴影部分),其中一条直角边在轴上,另一条直角边与轴垂直,则第100个等腰直角三角形的面积是( )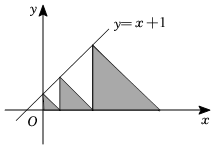 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 分解因式: .14. 不等式组的解集是 .15. 如图,和是以点为位似中心的位似图形.若 , 则与的周长比是 .
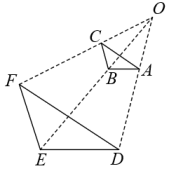 16. 若圆锥的底面圆半径为2,母线长为5,则该圆锥的侧面积是.(结果保留)17. 定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等弦圆”,现在有一个斜边长为2的等腰直角三角形,当等弦圆最大时,这个圆的半径为 .18. 如图,在正六边形中, , 是对角线上的两点,添加下列条件中的一个:①;②;③;④ . 能使四边形是平行四边形的是(填上所有符合要求的条件的序号).
16. 若圆锥的底面圆半径为2,母线长为5,则该圆锥的侧面积是.(结果保留)17. 定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等弦圆”,现在有一个斜边长为2的等腰直角三角形,当等弦圆最大时,这个圆的半径为 .18. 如图,在正六边形中, , 是对角线上的两点,添加下列条件中的一个:①;②;③;④ . 能使四边形是平行四边形的是(填上所有符合要求的条件的序号).
三、解答题
-
19. 计算:(1)、 .(2)、先化简,再求值: , 其中 , .20. 如图,在菱形ABCD中,CE=CF.求证:AE=AF.
 21. 2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校以中国传统节日端午节为契机,组织全体学生参加包粽子劳动体验活动,随机调查了部分学生,对他们每个人平均包一个粽子的时长进行统计,并根据统计结果绘制成如下不完整的统计图表.
21. 2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校以中国传统节日端午节为契机,组织全体学生参加包粽子劳动体验活动,随机调查了部分学生,对他们每个人平均包一个粽子的时长进行统计,并根据统计结果绘制成如下不完整的统计图表.等级
时长:(单位:分钟)
人数
所占百分比
4
20
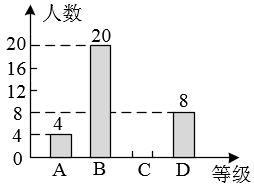
根据图表信息,解答下列问题:
(1)、本次调查的学生总人数为 , 表中的值为;(2)、该校共有500名学生,请你估计等级为的学生人数;(3)、本次调查中,等级为的4人中有两名男生和两名女生,若从中随机抽取两人进行活动感想交流,请利用画树状图或列表的方法,求恰好抽到一名男生和一名女生的概率.22. 如图是一座独塔双索结构的斜拉索大桥,主塔采用倒“Y”字形设计,某学习小组利用课余时间测量主塔顶端到桥面的距离.勘测记录如下表:
活动内容
测量主塔顶端到桥面的距离
成员
组长:××× 组员:××××××××××××
测量工具
测角仪,皮尺等
测量示意图

说明:左图为斜拉索桥的侧面示意图,点A、C,D,B在同一条直线上, , 点A,C分别与点B,D关于直线EF对称
测量数据
的大小
28°
AC的长度
84m
CD的长度
12m
请利用表中提供的信息,求主塔顶端E到AB的距离(参考数据: , , ).
23. 已知:如图,一次函数与反比例函数的图象有两个交点和 , 过点作轴,垂足为点;过点作轴,垂足为点 , 且点的坐标为 , 连接 . (1)、求的值;(2)、求四边形的面积.24. 如图,在中,为的直径,点E在上,D为的中点,连接并延长交于点C.连接 , 在的延长线上取一点F,连接 , 使 .
(1)、求的值;(2)、求四边形的面积.24. 如图,在中,为的直径,点E在上,D为的中点,连接并延长交于点C.连接 , 在的延长线上取一点F,连接 , 使 . (1)、求证:为的切线;(2)、若 , 求的半径.25. 如图(1),二次函数的图像与轴交于两点,与轴交于点,点的坐标为 , 点的坐标为 , 直线经过两点.
(1)、求证:为的切线;(2)、若 , 求的半径.25. 如图(1),二次函数的图像与轴交于两点,与轴交于点,点的坐标为 , 点的坐标为 , 直线经过两点. (1)、求该二次函数的表达式及其图像的顶点坐标;(2)、点为直线上的一点,过点作轴的垂线与该二次函数的图象相交于点 , 再过点作的垂线与该二次函数的图象相交于另一点 , 当时,求点的横坐标;(3)、如图(2),点关于轴的对称点为点 , 点为线段上的一个动点,连接 , 点为线段上一点,且 , 连接 , 当的值最小时,直接写出的长.
(1)、求该二次函数的表达式及其图像的顶点坐标;(2)、点为直线上的一点,过点作轴的垂线与该二次函数的图象相交于点 , 再过点作的垂线与该二次函数的图象相交于另一点 , 当时,求点的横坐标;(3)、如图(2),点关于轴的对称点为点 , 点为线段上的一个动点,连接 , 点为线段上一点,且 , 连接 , 当的值最小时,直接写出的长.