四川省攀枝花市2023年中考二模数学试卷
试卷更新日期:2023-06-19 类型:中考模拟
一、单选题
-
1. 在 , , , 这四个数中,最大的数是( )A、 B、 C、 D、2. 在如图所示的几何体中,主视图和俯视图相同的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 碳纳米管的硬度与金刚石相当,却拥有良好的柔韧性,可以拉伸,我国某物理所研究组已研制出直径为纳米的碳纳米管,1纳米米,则纳米用科学记数法表示为( )A、米 B、米 C、米 D、米5. 下列说法正确的是( )A、为了解春节期间河南省的空气质量,采用全面调查 B、射击运动员射击一次,命中靶心为必然事件 C、数据2,2,2,2,2的方差为0 D、数据6,8,6,13,8,12的众数为86. 两个直角三角板如图摆放,其中 , , , AB与DF交于点M.若 , 则的大小为( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 碳纳米管的硬度与金刚石相当,却拥有良好的柔韧性,可以拉伸,我国某物理所研究组已研制出直径为纳米的碳纳米管,1纳米米,则纳米用科学记数法表示为( )A、米 B、米 C、米 D、米5. 下列说法正确的是( )A、为了解春节期间河南省的空气质量,采用全面调查 B、射击运动员射击一次,命中靶心为必然事件 C、数据2,2,2,2,2的方差为0 D、数据6,8,6,13,8,12的众数为86. 两个直角三角板如图摆放,其中 , , , AB与DF交于点M.若 , 则的大小为( )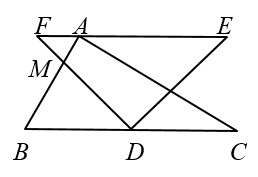 A、 B、 C、 D、7. 若关于x的方程的解是正数,则m的取值范围为( )A、 B、且 C、 D、且8. 如图所示的是A、B、C三点,按如下步骤作图:①先分别以A、B两点为圆心,以大于的长为半径作弧,两弧相交于M、N两点,作直线;②再分别以B、C两点为圆心,以大于的长为半径作弧,两弧相交于G、H两点,作直线 , 与交于点P,若 , 则等于( )
A、 B、 C、 D、7. 若关于x的方程的解是正数,则m的取值范围为( )A、 B、且 C、 D、且8. 如图所示的是A、B、C三点,按如下步骤作图:①先分别以A、B两点为圆心,以大于的长为半径作弧,两弧相交于M、N两点,作直线;②再分别以B、C两点为圆心,以大于的长为半径作弧,两弧相交于G、H两点,作直线 , 与交于点P,若 , 则等于( ) A、100° B、120° C、132° D、140°9. 在二次函数 , 与的部分对应值如下表:
A、100° B、120° C、132° D、140°9. 在二次函数 , 与的部分对应值如下表:…
-2
0
2
3
…
…
8
0
0
3
…
则下列说法:①图象经过原点;②图象开口向下;③当时,随的增大而增大;④图象经过点;⑤方程有两个不相等的实数根.其中正确的是( )
A、①②③④ B、①②③⑤ C、①②④⑤ D、①③④⑤10. 下列说法中正确的说法有( )个①对角线相等的四边形是矩形②在同圆或等圆中,同一条弦所对的圆周角相等③相等的圆心角所对的弧相等④平分弦的直径垂直于弦,并且平分弦所对的弧⑤到三角形三边距离相等的点是三角形三个内角平分线的交点
A、1 B、2 C、3 D、411. 如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H.则四边形EFGH的周长为( )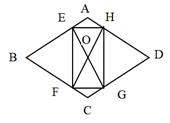 A、 B、 C、 D、12. 如图,矩形 中, ,以 为圆心,3为半径作 , 为 上一动点,连接 ,以 为直角边作 ,使 , ,则点 与点 的最小距离为( )
A、 B、 C、 D、12. 如图,矩形 中, ,以 为圆心,3为半径作 , 为 上一动点,连接 ,以 为直角边作 ,使 , ,则点 与点 的最小距离为( )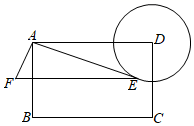 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 因式分解:.14. 如图,在正方形中,E为的中点,连接交于点F.若 , 则的面积为 .
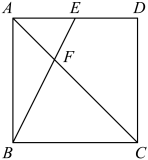 15. 已知关于x的一元二次方程mx2﹣4x+2=0有两个不相等的实数根,则m的取值范围是 .16. 如图,四边形是正方形,点E在的延长线上,连接 , 交于点F,连接 , 点H是的中点,连接 , 则下列结论中:①;②;③;④若 , 则的面积为 . 正确的是(填写所有正确结论的序号).
15. 已知关于x的一元二次方程mx2﹣4x+2=0有两个不相等的实数根,则m的取值范围是 .16. 如图,四边形是正方形,点E在的延长线上,连接 , 交于点F,连接 , 点H是的中点,连接 , 则下列结论中:①;②;③;④若 , 则的面积为 . 正确的是(填写所有正确结论的序号).
三、解答题
-
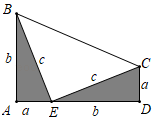
17. 计算18. 将两个全等的直角三角形按如图所示摆放,使点A、E、D在同一条直线上.利用此图的面积表示式证明勾股定理.
 19. 为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
19. 为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题: (1)、在这项调查中,共调查了多少名学生?(2)、请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;(3)、若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.20. 图(1)为某大型商场的自动扶梯、图(2)中的为从一楼到二楼的扶梯的侧面示意图.小明站在扶梯起点处时,测得天花板上日光灯的仰角为 , 此时他的眼睛与地面的距离 , 之后他沿一楼扶梯到达顶端后又沿()向正前方走了 , 发现日光灯刚好在他的正上方.已知自动扶梯的坡度为 , 的长度是 . (参考数据: , , )
(1)、在这项调查中,共调查了多少名学生?(2)、请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;(3)、若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.20. 图(1)为某大型商场的自动扶梯、图(2)中的为从一楼到二楼的扶梯的侧面示意图.小明站在扶梯起点处时,测得天花板上日光灯的仰角为 , 此时他的眼睛与地面的距离 , 之后他沿一楼扶梯到达顶端后又沿()向正前方走了 , 发现日光灯刚好在他的正上方.已知自动扶梯的坡度为 , 的长度是 . (参考数据: , , )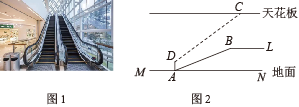 (1)、求图中到一楼地面的高度.(2)、求日光灯到一楼地面的高度.(结果精确到十分位)21. 如图,在平面直角坐标系中,一次函数的图象经过点 , 与反比例函数的图象交于点和点C.
(1)、求图中到一楼地面的高度.(2)、求日光灯到一楼地面的高度.(结果精确到十分位)21. 如图,在平面直角坐标系中,一次函数的图象经过点 , 与反比例函数的图象交于点和点C. (1)、求一次函数和反比例函数的表达式;(2)、若点P在y轴上,且的面积等于6,求点P的坐标.22. 如图,已知 , 为的直径,过点A作弦垂直于直径于点F,点B恰好为的中点,连接 .
(1)、求一次函数和反比例函数的表达式;(2)、若点P在y轴上,且的面积等于6,求点P的坐标.22. 如图,已知 , 为的直径,过点A作弦垂直于直径于点F,点B恰好为的中点,连接 . (1)、求证:;(2)、若 , 求的半径.23. 抛物线与x轴交于 , 两点,与y轴交于点C,直线y=kx-6经过点B.点P在抛物线上,设点P的横坐标为m.
(1)、求证:;(2)、若 , 求的半径.23. 抛物线与x轴交于 , 两点,与y轴交于点C,直线y=kx-6经过点B.点P在抛物线上,设点P的横坐标为m.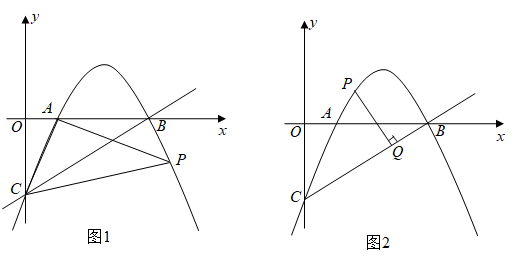 (1)、求抛物线的表达式和t,k的值;(2)、如图1,连接AC,AP,PC,若△APC是以CP为斜边的直角三角形,求点P的坐标;(3)、如图2,若点P在直线BC上方的抛物线上,过点P作PQ⊥BC,垂足为Q,求的最大值.24. 如图,在中, , D,E分别是边的中点,点P从点D出发沿方向以的速度运动,过点P作于Q,过点Q作交于R,交于G,当点Q与点C重合时,点P停止运动.设点P运动时间为 .
(1)、求抛物线的表达式和t,k的值;(2)、如图1,连接AC,AP,PC,若△APC是以CP为斜边的直角三角形,求点P的坐标;(3)、如图2,若点P在直线BC上方的抛物线上,过点P作PQ⊥BC,垂足为Q,求的最大值.24. 如图,在中, , D,E分别是边的中点,点P从点D出发沿方向以的速度运动,过点P作于Q,过点Q作交于R,交于G,当点Q与点C重合时,点P停止运动.设点P运动时间为 . (1)、点D到的距离的长是;(2)、令 , 求y关于t的函数关系式(不要求写出自变量的取值范围);(3)、是否存在点P,使为等腰三角形?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.
(1)、点D到的距离的长是;(2)、令 , 求y关于t的函数关系式(不要求写出自变量的取值范围);(3)、是否存在点P,使为等腰三角形?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.