四川省攀枝花市东区2023年中考二模数学试卷
试卷更新日期:2023-06-19 类型:中考模拟
一、单选题
-
1. 下列整式与为同类项的是( )A、 B、 C、 D、2. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算中,正确的是( )A、 B、 C、 D、4. 每年的4月7日是世界健康日,强调健康对于劳动创造和幸福生活的重要性,而血糖值(单位:)对于治疗疾病和观察疾病都有指导意义.某人在每天的早晨空腹自测血糖值,并将一周的数据绘制成如图所示的折线统计图,则这组数据的中位数和众数分别是( )
3. 下列计算中,正确的是( )A、 B、 C、 D、4. 每年的4月7日是世界健康日,强调健康对于劳动创造和幸福生活的重要性,而血糖值(单位:)对于治疗疾病和观察疾病都有指导意义.某人在每天的早晨空腹自测血糖值,并将一周的数据绘制成如图所示的折线统计图,则这组数据的中位数和众数分别是( )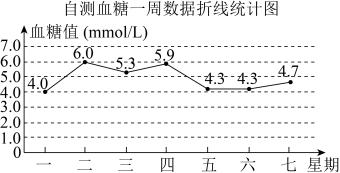 A、 , B、 , C、 , D、 ,5. 如图,在中,分别以 , 为圆心,大于长为半径作弧,两弧分别相交于 , 两点,作直线 , 分别交线段 , 于点 , , 若 , 的周长为11,则的长度为( )
A、 , B、 , C、 , D、 ,5. 如图,在中,分别以 , 为圆心,大于长为半径作弧,两弧分别相交于 , 两点,作直线 , 分别交线段 , 于点 , , 若 , 的周长为11,则的长度为( ) A、7 B、8 C、9 D、106. 下列二次根式中,不能与合并的是( )A、 B、 C、 D、7. 骑自行车是一种健康自然的运动旅游方式,长期坚持骑自行车可增强心血管功能,提高人体新陈代谢和免疫力.下图是骑行爱好者老刘2023年2月12日骑自行车行驶路程(km)与时间(h)的关系图象,观察图象得到下列信息,其中错误的是( )
A、7 B、8 C、9 D、106. 下列二次根式中,不能与合并的是( )A、 B、 C、 D、7. 骑自行车是一种健康自然的运动旅游方式,长期坚持骑自行车可增强心血管功能,提高人体新陈代谢和免疫力.下图是骑行爱好者老刘2023年2月12日骑自行车行驶路程(km)与时间(h)的关系图象,观察图象得到下列信息,其中错误的是( ) A、点表示出发4h,老刘共骑行80km B、老刘的骑行在0~2h的速度比3~4h的速度慢 C、0~2h老刘的骑行速度为15km/h D、老刘实际骑行时间为4h8. 用四根长度相等的木条制作学具,先制作图(1)所示的正方形 , 测得 , 活动学具成图(2)所示的四边形 , 测得 , 则图(2)中的长是( )
A、点表示出发4h,老刘共骑行80km B、老刘的骑行在0~2h的速度比3~4h的速度慢 C、0~2h老刘的骑行速度为15km/h D、老刘实际骑行时间为4h8. 用四根长度相等的木条制作学具,先制作图(1)所示的正方形 , 测得 , 活动学具成图(2)所示的四边形 , 测得 , 则图(2)中的长是( ) A、 B、 C、 D、9. 把不等式组中每个不等式的解集在同一条数轴上表示出来,正确的是( )A、
A、 B、 C、 D、9. 把不等式组中每个不等式的解集在同一条数轴上表示出来,正确的是( )A、 B、
B、 C、
C、 D、
D、 10. 有若干片相同的拼图,其形状如图1所示,且拼图沿水平方向排列时可紧密拼成一行,此时底部可与直线贴齐.当4片拼图紧密拼成一行时长度为 , 如图2所示.当10片拼图紧密拼成一行时长度为 , 如图3所示.设图1中的两部分的长度分别为 , , 则正确的是( )
10. 有若干片相同的拼图,其形状如图1所示,且拼图沿水平方向排列时可紧密拼成一行,此时底部可与直线贴齐.当4片拼图紧密拼成一行时长度为 , 如图2所示.当10片拼图紧密拼成一行时长度为 , 如图3所示.设图1中的两部分的长度分别为 , , 则正确的是( ) A、依题意, B、1片拼图的长度为 C、将拼图紧密拼成一行时,每增加一片拼图,总长度增加 D、将片拼图紧密拼成一行时,总长度为11. 如图,是半圆O的直径,是半圆上两点,点是弧的中点, , , 则弧的长为( )
A、依题意, B、1片拼图的长度为 C、将拼图紧密拼成一行时,每增加一片拼图,总长度增加 D、将片拼图紧密拼成一行时,总长度为11. 如图,是半圆O的直径,是半圆上两点,点是弧的中点, , , 则弧的长为( ) A、 B、 C、 D、12. 如图,在平面直角坐标系中,点A的坐标为(4,0),点Q是直线yx上的一个动点,以AQ为边,在AQ的右侧作等边△APQ,使得点P落在第一象限,连接OP,则OP+AP的最小值为( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中,点A的坐标为(4,0),点Q是直线yx上的一个动点,以AQ为边,在AQ的右侧作等边△APQ,使得点P落在第一象限,连接OP,则OP+AP的最小值为( ) A、6 B、4 C、8 D、6
A、6 B、4 C、8 D、6二、填空题
-
13. 分式方程的解是14. 学习电学知识后,小婷同学用四个开关 , 一个电源和一个灯泡设计了一个电路图,现任意闭合其中两个开关,则小灯泡发光的概率等于 .
 15. 若关于的一元二次方程有两个不相等的实数根,则的取值范围是 .16. 如图,将矩形沿折叠,使点落在边的点处,过点作交于点 , 连接 . 给出以下结论:(1);(2)四边形是菱形;(3);(4)当时,的长为 , 其中正确的是 . (只填序号)
15. 若关于的一元二次方程有两个不相等的实数根,则的取值范围是 .16. 如图,将矩形沿折叠,使点落在边的点处,过点作交于点 , 连接 . 给出以下结论:(1);(2)四边形是菱形;(3);(4)当时,的长为 , 其中正确的是 . (只填序号)
三、解答题
-
17. 先化简,再求值: , 其中18. 如图,在四边形中,相交于点O,O是的中点, .
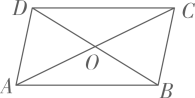 (1)、求证:四边形是平行四边形;(2)、若 , 求四边形的面积.19. 某校积极落实“双减”政策,将要开设拓展课程.为让学生可以根据自己的兴趣爱好选择最喜欢的课程,进行问卷调查,问卷设置以下四种选项:A(综合模型)、B(摄影艺术)、C(音乐鉴赏)、D(劳动实践),随机抽取了部分学生进行调查,每名学生必须且只能选择其中最喜欢的一种课程,并将调查结果整理绘制成如下不完整的统计图.
(1)、求证:四边形是平行四边形;(2)、若 , 求四边形的面积.19. 某校积极落实“双减”政策,将要开设拓展课程.为让学生可以根据自己的兴趣爱好选择最喜欢的课程,进行问卷调查,问卷设置以下四种选项:A(综合模型)、B(摄影艺术)、C(音乐鉴赏)、D(劳动实践),随机抽取了部分学生进行调查,每名学生必须且只能选择其中最喜欢的一种课程,并将调查结果整理绘制成如下不完整的统计图.
根据以上信息,解答下列问题:
(1)、此次被调查的学生人数为名;(2)、直接在答题卡中补全条形统计图;(3)、求拓展课程D(劳动实践)所对应的扇形的圆心角的度数;(4)、根据抽样调查结果,请你估计该校1500名学生中,有多少名学生最喜欢C(音乐鉴赏)拓展课程.20. 公园草坪上有一架秋千 , 秋千静止时,底端到地面的距离为 , 从坚直位置开始,向右可摆动的最大夹角为 , 已知秋千的长 . (1)、如图1,当向右摆动到最大夹角时,求到地面的距离;(2)、如图2,若有人在点右侧搭建了一个等腰帐篷,已知 , 帐篷的高为 , 秋千摆动的过程中是否会撞到帐篷?若不会撞到,请说明理由;若会撞到,则帐篷应该向右移动超过多少米才能不被撞到?21. 如图,在平面直角坐标系中,一次函数的图象与轴负半轴交于点 , 与轴交于点,与反比例函数交于 , 两点.
(1)、如图1,当向右摆动到最大夹角时,求到地面的距离;(2)、如图2,若有人在点右侧搭建了一个等腰帐篷,已知 , 帐篷的高为 , 秋千摆动的过程中是否会撞到帐篷?若不会撞到,请说明理由;若会撞到,则帐篷应该向右移动超过多少米才能不被撞到?21. 如图,在平面直角坐标系中,一次函数的图象与轴负半轴交于点 , 与轴交于点,与反比例函数交于 , 两点. (1)、求一次函数的解析式,并画出一次函数的图象;(2)、请直接写出不等式的解集;(3)、求的面积.22. 如图,是四边形的外接圆,是的直径, , 交的延长线于点平分 .
(1)、求一次函数的解析式,并画出一次函数的图象;(2)、请直接写出不等式的解集;(3)、求的面积.22. 如图,是四边形的外接圆,是的直径, , 交的延长线于点平分 . (1)、求证:是的切线;(2)、若 , 求的长.23. 问题提出:已知矩形 , 点为上的一点, , 交于点 . 将绕点顺时针旋转得到 , 则与有怎样的数量关系.
(1)、求证:是的切线;(2)、若 , 求的长.23. 问题提出:已知矩形 , 点为上的一点, , 交于点 . 将绕点顺时针旋转得到 , 则与有怎样的数量关系. (1)、【问题探究】
(1)、【问题探究】探究一:如图,已知正方形 , 点为上的一点, , 交于点 .
如图1,直接写出的值;(2)、将绕点顺时针旋转到如图所示的位置,连接、 , 猜想与的数量关系,并证明你的结论;(3)、探究二:如图,已知矩形 , 点为上的一点, , 交于点 .如图3,若四边形为矩形, , 将绕点顺时针旋转得到、的对应点分别为、点 , 连接、 , 则的值是否随着的变化而变化.若变化,请说明变化情况;若不变,请求出的值.
(4)、【一般规律】
如图3,若四边形为矩形, , 其它条件都不变,将绕点顺时针旋转得到 , 连接 , , 请直接写出与的数量关系.24. 如图,已知抛物线的图象与x轴交于点A(1,0),B(-3,0),与y轴的正半轴交于点C. (1)、求该抛物线的解析式;(2)、点D是线段上一动点,过点D作y轴的平行线,与交于点E,与抛物线交于点F.
(1)、求该抛物线的解析式;(2)、点D是线段上一动点,过点D作y轴的平行线,与交于点E,与抛物线交于点F.①连接 , 当的面积最大时,求此时点F的坐标;
②探究是否存在点D使得为直角三角形?若存在,求出点F的坐标;若不存在,说明理由.