四川省绵阳市游仙区2023年中考三模数学试卷

试卷更新日期：2023-06-19 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数-2023的相反数是（）

A、2023 B、-3202 C、 $\frac{1}{2023}$ D、 $- \frac{1}{2023}$

查看试题解析
2. “致中和，天地位焉，万物育焉.”对称美是我国古人和谐平衡思想的体现，常被运用于建筑、器物、绘画、标识等作品的设计上，使对称之美惊艳了千年的时光.在下列与扬州有关的标识或简图中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 2023年“五一”假日期间，群众出游热情高涨，四川省接待游客约4000万人次，实现旅游收入201.23亿元，其中4000万用科学记数法表示为（）

A、 $4 \times 1 0^{7}$ B、 $0.4 \times 1 0^{8}$ C、 $4 \times 1 0^{3}$ D、 $40 \times 1 0^{6}$

查看试题解析
4. 一副直角三角板( $∠ A C B = 30 °$ ， $∠ B E D = 45 °$ )按如图所示的位置摆放，如果 $A C ∥ D E$ ，那么 $∠ E B C$ 的度数是（）

A、 $15 °$ B、 $20 °$ C、 $30 °$ D、 $35 °$

查看试题解析
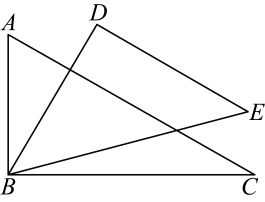5. 劳动教育是学校贯彻“五育并举”的重要举措，某校倡议学生在家做一些力所能及的家务劳动．李老师为了解学生每周参加家务劳动的时间，随机调查了本班 $20$ 名学生，收集到如下数据：
时间/h
6
5
4
3
2
人数/名
2
6
4
6
2
关于家务劳动时间的描述正确的是（）

A、众数是6 B、平均数是4 C、中位数是3 D、方差是1

查看试题解析
6. 与 $\sqrt{2} \times (\sqrt{40} - \sqrt{2})$ 最接近的整数是（）

A、4 B、5 C、6 D、7

查看试题解析
7. 游仙是三国故地，古绵治所，历史悠久，风景优美．富乐山，越王楼，仙海风景区，绵阳科技馆已是游仙响亮的代名词．某校课外兴趣小组设计了4张旅游宣传卡片，正面图案如图所示，它们除此之外完全相同．将这4张卡片背面朝上，洗匀，从中随机抽取两张，则抽取的卡片正面图案恰好是“富乐山”和“越王楼”的概率为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
8. 某地突发地震，为了紧急安置40名地震灾民，需要搭建可容纳6人或4人的帐篷，若所搭建的帐篷恰好 $($ 既不多也不少 $)$ 能容纳这40名灾民，则不同的搭建方案有（）

A、2种 B、3种 C、4种 D、6种

查看试题解析
9. 已知关于x的方程 $4 x^{2} - (k + 5) x - k - 9 = 0$ 有两个不相等的实数根 $x_{1}$ ， $x_{2}$ ，且 $x_{1} = - 1$ ， $0 < x_{2} < 1$ ，则k的取值范围是（）

A、 $- 18 < k < - 10$ B、 $0 < k < 8$ C、 $- 9 < k < - 5$ D、 $- 18 < k < - 10$ 且 $k \neq - 13$

查看试题解析
10. 如图，已知△ABC的顶点坐标分别为A(0，2)，B(1，0)，C(2，1).若二次函数y=x²+bx+1的图像与阴影部分(含边界)一定有公共点，则实数b的取值范围是（）

A、b≤-2 B、b<-2 C、b≥-2 D、b>-2

查看试题解析
11. 如图，直角三角形 $B E F$ 顶点 $F$ 在矩形 $A B C D$ 的对角线 $A C$ 上运动，连接 $A E$ ． $∠ E B F = ∠ A C D$ ， $A B = 6$ ， $B C = 8$ ，则 $A E$ 的最小值为（）．

A、 $\frac{54}{25}$ B、 $\frac{12}{5}$ C、 $\frac{14}{5}$ D、 $\frac{72}{25}$

查看试题解析
12. 如图，等边 $Δ A B C$ 的边长为3，点D在边 $A C$ 上， $A D = \frac{1}{2}$ ，线段 $P Q$ 在边 $B A$ 上运动， $P Q = \frac{1}{2}$ ，有下列结论：

① $C P$ 与 $Q D$ 可能相等；② $Δ A Q D$ 与 $Δ B C P$ 可能相似；③四边形 $P C D Q$ 面积的最大值为 $\frac{31 \sqrt{3}}{16}$ ；④四边形 $P C D Q$ 周长的最小值为 $3 + \frac{\sqrt{37}}{2}$ .其中，正确结论的序号为（）

A、①④ B、②④ C、①③ D、②③

查看试题解析

二、填空题

13. 多项式 $2 m^{2} n + 6 m n - 4 m^{3} n$ 的公因式是．

查看试题解析
14. 如图，在平面直角坐标系中，以原点O为中心，把点 $A (2 ， 1)$ 顺时针旋转 $90 °$ 得到点 $B (x ， y)$ ，则 $x + y$ 的值为．

查看试题解析
15. 某水上乐园在一平地推出了“急流勇进”的项目，项目有两条斜坡滑道以满足不同的难度需求，游客可以乘坐垂直升降电梯 $A B$ 自由上下选择项目难度．其中斜坡轨道 $B C$ 的坡度为 $i = 5 ： 12$ ， $B C = 13$ 米， $C D = 16$ 米， $∠ D = 32 °$ （其中点A、B、C、D均在同一平面内），则垂直升降电梯 $A B$ 的高度约为米．（参考数据： $s i n 32 ° \approx 0.530$ ， $c o s 32 ° \approx 0.848$ ， $t a n 32 ° \approx 0.625$ ）

查看试题解析
16. 如图所示，扇形 $O A B$ 中 $∠ A O B = 120 ° ， O B = 2$ ，点C为 $\overset{⌢}{A B}$ 的中点，点D为 $A O$ 的中点，连接 $A B ， C D$ 交于点P，则阴影部分图形的面积是（结果保留 $π$ ）．

查看试题解析
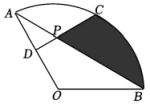17. 若关于x的一元一次不等式组 ${\begin{array}{l} \frac{x - 2}{3} < x + 1 \\ x + a \leq 3 \end{array}$ 至少有2个整数解，且关于y的分式方程 $\frac{y - a}{y - 2} + \frac{1}{2 - y} = - 1$ 的解是正整数，则所有满足条件的整数a的值之积是．

查看试题解析
18. 如图，正方形ABCD中，AD＝6，点E是对角线AC上一点，连接DE，过点E作EF⊥ED，交AB于点F，连接DF，交AC于点G，将△EFG沿EF翻折，得到△EFM，连接DM，交EF于点N，若AF=2，则 $Δ E M N$ 的面积为__．

查看试题解析

三、解答题

19.

(1)、计算： ${(\sqrt{3})}^{2} + {(4 - π)}^{0} - | - 3 | + \sqrt{2} c o s 45 °$ ．

(2)、先化简，再求值： $(x - 1 - \frac{3}{x + 1}) \div \frac{x^{2} + 4 x + 4}{x + 1}$ ，其中 $x = | 1 - \sqrt{2} | - 2 c o s 60 °$ ．

查看试题解析
20. 天舟六号是世界现役运输能力最大的货运飞船，5月10日，由中国航天科技集团五院研制的天舟六号货运飞船由长征七号遥七运载火箭发射升空，随后顺利进入预定轨道，发射任务取得圆满成功．为庆祝我国航天事业取得的辉煌成就，学校开展了航天知识竞赛活动，为了解全校学生竞赛成绩的情况，随机抽取了一部分学生的成绩，分成四组：A组（ $60 \leq x < 70$ ）；B组（ $70 \leq x < 80$ ）；C组（ $80 \leq x < 90$ ）；D组（ $90 \leq x < 100$ ），并绘制出如图不完整的统计图．

(1)、求被抽取的学生成绩在C组的有多少人？并把条形统计图补完整；

(2)、若该学校有1500名学生，估计这次竞赛成绩在A组的学生有多少人？

(3)、现学校为获得最高分的甲、乙、丙三名同学颁发荣誉证书，在不知道证书内姓名的情况下随机发给三名同学，请用列表法或树状图法求出每个同学拿到的证书恰好都是自己的概率．

查看试题解析
21. 2011年以来，绵阳已蝉联4届“全国文明城市”，这一荣誉已经成为绵阳最靓丽的一张“城市名片”．今年，我市继续积极开展创建全国文明城市八大攻坚行动，某街道积极响应，决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱，若购买4个垃圾箱比购买5个温馨提示牌多350元，垃圾箱的单价是温馨提示牌单价的3倍．

(1)、求垃圾箱和温馨提示牌的单价各是多少元？

(2)、如果该街道需购买温馨提示牌和垃圾箱共3000个．
①求购买温馨提示牌和垃投箱所需费用w（元）与温馨提示牌的个数m的函数关系式；
②若该街道计划购买温馨提示牌与垃圾箱的总费用不超过35万元，而且垃圾箱的个数不少于温馨提示牌的个数的0.5倍，问：该街道所购买的温馨提示牌多少个时，所需费用最省？最省费用是多少．

查看试题解析
22. 如图，已知菱形 $A B C D$ 中， $∠ A B C = 60 °$ ， E，F分别在边 $A B$ ， $A D$ 上， $△ E C F$ 是等边三角形，对角线 $A C$ 交 $E F$ 于点M，点N在 $A C$ 上，且 $A N = B E$ ．

(1)、求证： $∠ B C E = ∠ F C M$ ；

(2)、若 $B C = 3$ ， $B E = 1$ ，求 $M N$ 的值．

查看试题解析
23. 如图，在平面直角坐标系中，矩形 $O A B C$ 的顶点B的坐标为 $(8 ， 4)$ ， $O A$ ， $O C$ 分别落在x轴和y轴上，将 $△ O A B$ 绕点O逆时针旋转，使点B落在y轴上，得到 $△ O D E$ ， $O D$ 与 $C B$ 相交于点F，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过点F，交 $A B$ 于点G．

(1)、求k的值；

(2)、若点P在坐标轴上运动，求动点P的坐标，使 $S_{△ P F G} = S_{△ B F G}$ ．

查看试题解析
24. 如图， $A B$ 为 $⊙ O$ 的直径，C为 $⊙ O$ 上一点，F为 $⊙ O$ 过点B的切线上的一点，连接 $A F$ 、 $B C$ 交于点E， $A F$ 交 $⊙ O$ 于点D， $∠ C B F = 2 ∠ B A F$ ．

(1)、求证：点D为弧 $B C$ 的中点；

(2)、连接 $B D$ ，过点D作 $D G ⊥ A B$ 于点H，交 $⊙ O$ 于点G，连接 $C G$ ，交 $A D$ 于点N，求证： $C N + B D = N G$ ．

(3)、在（2）的条件下， $C N = 6$ ， $t a n ∠ G = \frac{1}{2}$ ，求 $⊙ O$ 的半径．

查看试题解析
25. 如图，二次函数的图象分别交x轴于点 $A (- 1 ， 0)$ 、点 $B (m ， 0)$ ，交y轴于点 $C (0 ， m)$ （其中 $m > 1$ ），连接 $A C$ 、 $B C$ ，点D为 $△ A B C$ 的外心，连接 $A D$ 、 $B D$ 、 $C D$ ．

(1)、求这条抛物线的解析式（用含m的代数式表示）；

(2)、若 $△ C D B$ 的面积为 $\frac{\sqrt{5}}{2}$ ，请求出m的值；

(3)、在（2）的条件下，连接 $O D$ ，在直线 $B C$ 上是否存在一点P，使得以点B、D、P为顶点的三角形与 $△ A O D$ 相似，若存在，求出点P的纵坐标，若不存在，请说明理由．

查看试题解析

时间/h	6	5	4	3	2
人数/名	2	6	4	6	2