四川省绵阳市三台县2023年中考三模数学试卷
试卷更新日期:2023-06-19 类型:中考模拟
一、单选题
-
1. 实数﹣2023的绝对值是( )A、2023 B、﹣2023 C、 D、2. 如图是由6个完全相同的小正方体组成的几何体,其俯视图为( )
 A、
A、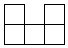 B、
B、 C、
C、 D、
D、 3. 我国古代数学家祖冲之推算出的近似值为 , 它与的误差小于0.0000003.将0.0000003用科学记数法可以表示为( )A、 B、 C、 D、4. 如图,在矩形中, , , 是矩形的对称中心,点、分别在边、上,连接、 , 若 , 则的值为( )
3. 我国古代数学家祖冲之推算出的近似值为 , 它与的误差小于0.0000003.将0.0000003用科学记数法可以表示为( )A、 B、 C、 D、4. 如图,在矩形中, , , 是矩形的对称中心,点、分别在边、上,连接、 , 若 , 则的值为( ) A、 B、 C、 D、5. 如图,把直角三角形ABO放置在平面直角坐标系中,已知 ,B点的坐标为 ,将 沿着斜边AB翻折后得到 ,则点C的坐标是( )
A、 B、 C、 D、5. 如图,把直角三角形ABO放置在平面直角坐标系中,已知 ,B点的坐标为 ,将 沿着斜边AB翻折后得到 ,则点C的坐标是( )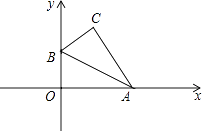 A、 B、 C、 D、6. 如图,正六边形的边长为2,以A为圆心,的长为半径画弧,得 , 连接 , , 则图中阴影部分的面积为( )
A、 B、 C、 D、6. 如图,正六边形的边长为2,以A为圆心,的长为半径画弧,得 , 连接 , , 则图中阴影部分的面积为( )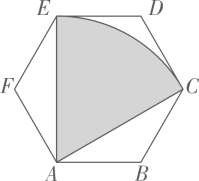 A、 B、 C、 D、7. 若关于的方程的两个实数根满足关系式 , 则的值为( )A、11 B、-1 C、11或-1 D、11或-1或18. 某校篮球队有20名队员,统计所有队员的年龄制作如下表格:对于不同的 , 下列统计量中不会发生改变的是( )
A、 B、 C、 D、7. 若关于的方程的两个实数根满足关系式 , 则的值为( )A、11 B、-1 C、11或-1 D、11或-1或18. 某校篮球队有20名队员,统计所有队员的年龄制作如下表格:对于不同的 , 下列统计量中不会发生改变的是( )年龄(岁)
16
15
14
13
12
人数
2
9
1
A、中位数,众数 B、平均数,方差 C、平均数,中位数 D、众数,方差9. 幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图(1)就是一个幻方.图(2)是一个未完成的幻方,则与的和是( )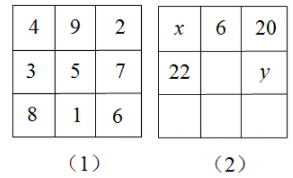 A、9 B、10 C、11 D、1210. 如图1,动点P从矩形ABCD的顶点A出发,在边AB,BC上沿A→B→C的方向,以1cm/s的速度匀速运动到点C,的面积S(cm2)随运动时间t(s)变化的函数图象如图2所示,则AB的长是( )
A、9 B、10 C、11 D、1210. 如图1,动点P从矩形ABCD的顶点A出发,在边AB,BC上沿A→B→C的方向,以1cm/s的速度匀速运动到点C,的面积S(cm2)随运动时间t(s)变化的函数图象如图2所示,则AB的长是( ) A、 B、 C、 D、11. 如图,已知开口向下的抛物线与x轴交于点 , 对称轴为直线.则下列结论正确的有( )
A、 B、 C、 D、11. 如图,已知开口向下的抛物线与x轴交于点 , 对称轴为直线.则下列结论正确的有( )①;
②函数的最大值为;
③若关于x的方程无实数根,则;
④代数式.
 A、1个 B、2个 C、3个 D、4个12. 已知点O是边长为6的等边△ABC的中心,点P在△ABC外,△ABC,△PAB,△PBC,△PCA的面积分别记为 , , , . 若 , 则线段OP长的最小值是( )A、 B、 C、 D、
A、1个 B、2个 C、3个 D、4个12. 已知点O是边长为6的等边△ABC的中心,点P在△ABC外,△ABC,△PAB,△PBC,△PCA的面积分别记为 , , , . 若 , 则线段OP长的最小值是( )A、 B、 C、 D、二、填空题
-
13. 因式分解:4x3﹣12x2+9x= .14. 如图,E为的边延长线上一点,过点E作.若 , , 则.
 15. 若二次根式有意义,且关于x的分式方程有正整数解,则符合条件的整数m的和是.16. 小丽测量了斜坡上一棵垂直于地面的大树的高度.如图,小丽先在坡角为的斜坡上的点处,测得树尖的仰角为 , 然后沿斜坡走了10米到达坡脚处,又在水平路面上行走20米到达大树所在的斜坡坡脚处,大树所在斜坡的坡度 , 且大树与坡脚的距离为15米,则大树的高度约为 . 参考数据: , , , . (结果精确到0.1)
15. 若二次根式有意义,且关于x的分式方程有正整数解,则符合条件的整数m的和是.16. 小丽测量了斜坡上一棵垂直于地面的大树的高度.如图,小丽先在坡角为的斜坡上的点处,测得树尖的仰角为 , 然后沿斜坡走了10米到达坡脚处,又在水平路面上行走20米到达大树所在的斜坡坡脚处,大树所在斜坡的坡度 , 且大树与坡脚的距离为15米,则大树的高度约为 . 参考数据: , , , . (结果精确到0.1) 17. 不等式组的解集是 , 则的取值范围是 .18. 如图,在中, , , F是上一点,分别过点C、B作的垂线,垂足为E、D,若 , , 则的长为 .
17. 不等式组的解集是 , 则的取值范围是 .18. 如图,在中, , , F是上一点,分别过点C、B作的垂线,垂足为E、D,若 , , 则的长为 .
三、解答题
-
19.(1)、计算:(2)、先化简,再求值: , 其中.20. 6月5日是世界环境日.某校举行了环保知识竞赛,从全校学生中随机抽取了n名学生的成绩进行分析,并依据分析结果绘制了不完整的统计表和统计图(如下图所示).
学生成绩分布统计表
成绩/分
组中值
频率
75.5≤x<80.5
78
0.05
80.5≤x<85.5
83
a
85.5≤x<90.5
88
0.375
90.5≤x<95.5
93
0.275
95.5≤x<100.5
98
0.05
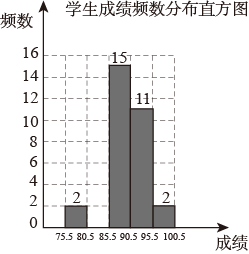
请根据以上图表信息,解答下列问题:
(1)、填空:n= , a=;(2)、请补全频数分布直方图;(3)、求这n名学生成绩的平均分;(4)、从成绩在75.5≤x<80.5和95.5≤x<100.5的学生中任选两名学生.请用列表法或画树状图的方法,求选取的学生成绩在75.5≤x<80.5和95.5≤x<100.5中各一名的概率.21. 某中学准备购进、两种教学用具共40件,种每件价格比种每件贵6元,同时购进3件种教学用具和2件种教学用具恰好用去113元.(1)、求购买5件和8件两种教学用具共用了多少元?(2)、学校准备用不少于830元且不多于850元的金额购买、两种教学用具,问至少能购买多少件种教学用具?22. 定义:我们把一组对边平行另一组对边相等且不平行的四边形叫做等腰梯形.(1)、如图1,已知四边形是矩形,以为一边作等腰梯形 , , 连接、.求证:; (2)、如图2,的对角线、交于点O, , , 过点O作的垂线交的延长线于点 , 连接.若 , 求的长.
(2)、如图2,的对角线、交于点O, , , 过点O作的垂线交的延长线于点 , 连接.若 , 求的长. 23. 如图,一次函数的图象与反比例函数的图象交于点A,与x轴交于点B,与y轴交于点C,轴于点D, , 点C关于直线的对称点为点E.
23. 如图,一次函数的图象与反比例函数的图象交于点A,与x轴交于点B,与y轴交于点C,轴于点D, , 点C关于直线的对称点为点E.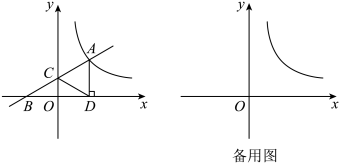 (1)、点E是否在这个反比例函数的图象上?请说明理由;(2)、连接、 , 若四边形为正方形.点P在y轴上,当最大时,求点P的坐标.24. 如图,点E,F分别为矩形边 , 上的点,以为直径作交于点G,且与相切,连接 .
(1)、点E是否在这个反比例函数的图象上?请说明理由;(2)、连接、 , 若四边形为正方形.点P在y轴上,当最大时,求点P的坐标.24. 如图,点E,F分别为矩形边 , 上的点,以为直径作交于点G,且与相切,连接 . (1)、若 , 求证: .(2)、若 , , 连接 , 若是以为腰的等腰三角形,求所有满足条件的的长.(3)、连接 , 若的延长线经过点A,且 , 求的值.25. 如图,已知二次函数的图像交轴于点 , , 交轴于点 .
(1)、若 , 求证: .(2)、若 , , 连接 , 若是以为腰的等腰三角形,求所有满足条件的的长.(3)、连接 , 若的延长线经过点A,且 , 求的值.25. 如图,已知二次函数的图像交轴于点 , , 交轴于点 . (1)、求这个二次函数的表达式;(2)、如图 , 点从点出发,以每秒个单位长度的速度沿线段向点运动,点从点出发,以每秒个单位长度的速度沿线段向点运动,点 , 同时出发.设运动时间为秒().当为何值时,的面积最大?最大面积是多少?(3)、已知是抛物线上一点,在直线上是否存在点 , 使以 , , , 为顶点的四边形是平行四边形?若存在,直接写出点坐标;若不存在,请说明理由.
(1)、求这个二次函数的表达式;(2)、如图 , 点从点出发,以每秒个单位长度的速度沿线段向点运动,点从点出发,以每秒个单位长度的速度沿线段向点运动,点 , 同时出发.设运动时间为秒().当为何值时,的面积最大?最大面积是多少?(3)、已知是抛物线上一点,在直线上是否存在点 , 使以 , , , 为顶点的四边形是平行四边形?若存在,直接写出点坐标;若不存在,请说明理由.