四川省乐山市峨眉山市2023年中考二模数学试卷

试卷更新日期：2023-06-19 类型：中考模拟

进入出卷网下载

一、单选题

1. -5的相反数是（）

A、5 B、-5 C、 $\frac{1}{5}$ D、 $- \frac{1}{5}$

查看试题解析
2. 如图所示几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 华为Mate21手机搭载了全球首款7纳米制程芯片，7纳米就是0.000000007米，数据0.000000007用科学记数法表示为（）．

A、 $7 \times 1 0^{- 8}$ B、 $0.7 \times 1 0^{- 9}$ C、 $7 \times 1 0^{- 9}$ D、 $7 \times 1 0^{- 10}$

查看试题解析
4. 下列运算正确的是（）

A、 $a^{2} + a = a^{3}$ B、 ${(a^{2})}^{3} = a^{5}$ C、 $a^{8} \div a^{2} = a^{4}$ D、 $a^{2} \cdot a^{3} = a^{5}$

查看试题解析
5. 某中学为了解七年级550名学生的睡眠情况，抽查了其中的200名学生的睡眠时间进行统计，下面叙述正确的是（）

A、以上调查属于全面调查 B、总体是七年级550名学生 C、所抽取的200名学生是总体的一个样本 D、每名学生的睡眠时间是一个个体

查看试题解析
6. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = B C$ ，按以下步骤作图：①以点 $A$ 为圆心，以任意长为半径作弧，分别交 $A C$ ， $A B$ 于点 $M$ ， $N$ ；②分别以 $M$ ， $N$ 为圆心，以大于 $\frac{1}{2}$ $M N$ 的长为半径作弧，两弧在 $∠ B A C$ 内交于点 $O$ ；③作射线 $A O$ ，交 $B C$ 于点 $D$ ．若点 $D$ 到 $A B$ 的距离为 $2$ ，则 $B C$ 的长为（）

A、 $2 + \sqrt{2}$ B、 $2 + 2 \sqrt{2}$ C、 $2 \sqrt{2}$ D、 $2 \sqrt{2} - 2$

查看试题解析
7. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 58 °$ ．以 $B C$ 为直径的 $⊙ O$ 交 $A B$ 于点 $D$ ， $E$ 是⊙O上一点，且弧 $C E = C D$ ，连接 $O E$ ．过点 $E$ 作 $E F$ ⊥ $O E$ ，交 $A C$ 的延长线于点 $F$ ，则 $∠ F$ 的度数为（）

A、 $112 °$ B、 $114 °$ C、 $116 °$ D、 $118 °$

查看试题解析
8. 我国古代数学古典名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”其大意是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量，木条还剩余1尺；问长木多少尺？如果设木条长为x尺，绳子长为y尺，则下面所列方程组正确的是（）

A、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} y = x - 1 \end{array}$ B、 ${\begin{array}{l} y = x - 4.5 \\ \frac{1}{2} y = x + 1 \end{array}$ C、 ${\begin{array}{l} y = x + 4.5 \\ 2 y = x - 1 \end{array}$ D、 ${\begin{array}{l} y = x - 4.5 \\ 2 y = x + 1 \end{array}$

查看试题解析
9. 如图，菱形 $A B C D$ 中， $A B = 4$ ， $∠ A D C = 120 °$ ， $E$ 是对角线 $A C$ 上的任意一点，则 $\frac{1}{2} C E + B E$ 的最小值为（）．

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、2 D、 $2 \sqrt{3} - 1$

查看试题解析
10. 如图，矩形 $A B C D$ 中，点A在双曲线 $y = - \frac{8}{x}$ 上，点 $B$ ， $C$ 在x轴上，延长 $C D$ 至点 $E$ ，使 $C D = 2 D E$ ，连接 $B E$ 交y轴于点 $F$ ，连接 $C F$ ，则 $△ B F C$ 的面积为（）

A、6 B、7 C、8 D、9

查看试题解析

二、填空题

11. 若 $\sqrt{x - 8}$ 在实数范围内有意义，则实数x的取值范围是．

查看试题解析

12. 为了参加中学生篮球联赛，某校篮球队准备购买10双运动鞋收集尺码，并整理如下统计表：

尺码/ $c m$	25	25.5	26	26.5	27
购买量/双	1	2	3	2	2

则这组数据的中位数是．

查看试题解析

13. 若一个圆锥的底面积为 $9 π$ ，锥高为4，则这个圆锥侧面展开的扇形面积为．

查看试题解析
14. “南昌之星”摩天轮，位于江西省南昌市红谷滩新区红角洲赣江边上的赣江市民公园，摩天轮高160m（最高点到地面的距离）．如图，点O是摩天轮的圆心，AB是其垂直于地面的直径，小贤在地面点C处利用测角仪测得摩天轮的最高点A的仰角为45°，测得圆心O的仰角为30°，则摩天轮的半径为m ．（结果保留根号）

查看试题解析
15. 某动物园利用杠杆原理称象：如图，在点P处挂一根质地均匀且足够长的钢梁（呈水平状态），将装有大象的铁笼和弹簧秤（秤的重力忽略不计）分别悬挂在钢梁的点A，B处，当钢梁保持水平时，弹簧秤读数为k（N）．若铁笼固定不动，移动弹簧秤使 $B P$ 扩大到原来的n（ $n > 1$ ）倍，且钢梁保持水平，则弹簧秤读数为（N）（用含n，k的代数式表示）．

查看试题解析

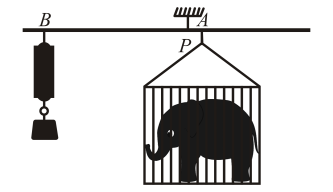
三、解答题

16. 已知二次函数 $y = a (x - 1) (x - 1 - a)$ （ $a$ 为常数，且 $a \neq 0$ ）．

(1)、若点 $(0 ， y_{1})$ ， $(3 ， y_{2})$ 在函数图象上，则 $y_{1}$ $y_{2}$ （填“>”、“<”或“=”）；

(2)、当 $0 < x < 3$ 时， $y < 2$ ，则 $a$ 的取值范围是．

查看试题解析
17. $\sqrt{12} + | 2 \sqrt{3} - 3 | - 2 t a n 60 ° - {(\sqrt{3})}^{2} + {(π - 2023)}^{0}$ ．

查看试题解析
18. 解不等式组 ${\begin{matrix} 3 (x - 1) < 5 x + 1 \\ \frac{x - 1}{2} \geq 2 x - 4 \end{matrix}$ ，并求出 $x$ 的最小整数解.

查看试题解析
19. 先化简，再求值： $(1 + \frac{1}{x + 1}) \div \frac{x^{2} - 4}{2 x + 2}$ ，其中 $x$ 是一元二次方程 $x^{2} - 1 = 0$ 的解．

查看试题解析
20.
已知△ABN和△ACM位置如图所示，AB=AC，AD=AE，∠1=∠2．

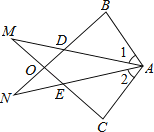(1)、求证：BD=CE；

(2)、求证：∠M=∠N．

查看试题解析
21. 为全面贯彻党的教育方针，坚持“健康第一”的教育理念，促进学生健康成长，提高体质健康水平，某市调整体育中考实施方案：分值增加至70分，男生1000米（女生800米）必考，足球、篮球、排球“三选一”……，从2020年起开始实施．某中学为了解七年级学生对三大球类运动的喜爱情况，从七年级学生中随机抽取部分学生进行问卷调查，通过分析整理绘制了如下两幅统计图，请根据两幅统计图中的信息解答下列问题：

(1)、求参与调查的学生中，喜爱排球运动的学生人数，并补全条形图；

(2)、若该中学七年级共有260名学生，请你估计该中学七年级学生中喜爱篮球运动的学生有多少人？

(3)、若从喜爱足球运动的2名男生和2名女生中随机抽取2名学生，确定为县足球队运动员的重点培养对象，请用列表法或画树状图的方法求抽取的两名学生为1名男生和1名女生的概率．

查看试题解析
22. 如图，在平面直角坐标系中，一次函数 $y_{1} = k x + b (k \neq 0)$ 的图象与反比例函数 $y_{2} = \frac{m}{x} (m \neq 0)$ 的图象相交于第一、三象限内的 $A (3 ， 5) ， B (a ， - 3)$ 两点，与 $x$ 轴交于点 $C$ .

(1)、求该反比例函数和一次函数的解析式；

(2)、在 $y$ 轴上找一点 $P$ 使 $P B - P C$ 最大，求 $P B - P C$ 的最大值及点 $P$ 的坐标；

(3)、直接写出当 $y_{1} > y_{2}$ 时， $x$ 的取值范围.

查看试题解析
23. 在平面直角坐标系 $x o y$ 中，已知点 $M (a ， b)$ ， $N$ ．对于点 $P$ 给出如下定义：将点 $P$ 先向右 $(a \geq 0)$ 或向左 $(a < 0)$ 平移 $| a |$ 个单位长度，再向上 $(b \geq 0)$ 或向下 $(b < 0)$ 平移 $| b |$ 个单位长度，得到点 $P^{'}$ ，点 $P^{'}$ 关于点 $N$ 的对称点为 $Q$ ，称点 $Q$ 为点 $P$ 的“欢乐点”．

(1)、如图，点 $M$ $(1 ， 1)$ ，点 $N (2 ， 2)$ 在线段 $O M$ 的延长线上．若点 $P$ $(- 2 ， 0)$ ，点 $Q$ 为点 $P$ 的“欢乐点”．
①在图中画出点 $P^{'}$ 与点 $Q$ ；
②连接 $P Q$ ，交线段 $O N$ 于点 $T$ ，求证： $N T$ ＝ $\frac{1}{2}$ $O M$ ；

(2)、⊙O的半径为1， $M$ 是⊙O上一点，点 $N$ 在线段 $O M$ 上，且 $O N$ ＝ $t$ （ $\frac{1}{2}$ ＜ $t$ ＜1），若 $P$ 为⊙O外一点，点 $Q$ 为点P的“欢乐点”，连接 $P Q$ ．当点 $M$ 在⊙O上运动时，直接写出 $P Q$ 长的最大值与最小值的差（用含 $t$ 的式子表示）．

查看试题解析
24. 如图， $A B$ 是 $⊙ O$ 的直径， $C$ 、 $D$ 是 $⊙ O$ 上两点，且 $\hat{B D} = \hat{C D}$ ，过点 $D$ 的直线 $D E ⊥ A C$ 交 $A C$ 的延长线于点 $E$ ，交 $A B$ 的延长线于点 $F$ ，连接 $A D$ 、 $O E$ 交于点 $G$ ．

(1)、求证： $D E$ 是 $⊙ O$ 的切线；

(2)、若 $\frac{D G}{A G} = \frac{2}{3}$ ， $⊙ O$ 的半径为2，求阴影部分的面积；

(3)、连结 $B E$ ，在（2）的条件下，求 $B E$ 的长．

查看试题解析
25. 【问题情境】：
数学活动课上，同学们开展了以折叠为主题的探究活动，如图1，已知矩形纸片 $A B C D (A D > A B)$ ，其中宽 $A B = 8$ ．

(1)、【动手实践】：
如图1，威威同学将矩形纸片 $A B C D$ 折叠，点 $A$ 落在 $B C$ 边上的点 $M$ 处，折痕为 $B N$ ，连接 $M N$ ，然后将纸片展平，得到四边形 $A B M N$ ，则折痕 $B N$ 的长度为．

(2)、【探究发现】：
如图2，胜胜同学将图1中的四边形 $A B M N$ 剪下，取 $A N$ 边中点 $E$ ，将 $△ A B E$ 沿 $B E$ 折叠得到 $△ A^{^{'}} B E$ ，延长 $B A^{'}$ 交 $M N$ 于点 $F$ ．点 $Q$ 为 $B M$ 边的中点，点 $P$ 是边 $M N$ 上一动点，将 $△ M Q P$ 沿 $P Q$ 折叠，当点 $M$ 的对应点 $M^{'}$ 落在线段 $B F$ 上时，求此时 $t a n ∠ P Q M$ 的值；

(3)、【反思提升】：
明明同学改变图2中 $Q$ 点的位置，即点 $Q$ 为 $B M$ 边上一动点，点 $P$ 仍是边 $M N$ 上一动点，按照（2）中方式折叠 $△ M Q P$ ，使点 $M^{'}$ 落在线段 $B F$ 上，明明同学不断改变点 $Q$ 的位置，发现在某一位置 $∠ Q P M$ 与（2）中的 $∠ P Q M$ 相等，请直接写出此时 $B Q$ 的长度．

查看试题解析
26. 如图，已知二次函数 $y = a x^{2} + b x + 4$ 的图像与 $x$ 轴交于 $A (- 2 ， 0)$ ， $B (4 ， 0)$ 两点，与 $y$ 轴交于点 $C$ ，抛物线的顶点为 $D$ ，点 $P$ 是 $x$ 轴上方抛物线上的一个动点，过 $P$ 作 $P N$ $⊥$ $x$ 轴于 $N$ ，交直线 $B C$ 于 $M$ ．

(1)、求二次函数表达式及顶点 $D$ 的坐标；

(2)、当 $P M = M N$ 时，求点 $P$ 的坐标；

(3)、设抛物线对称轴与 $x$ 轴交于点 $H$ ，连接 $A P$ 交对称轴于 $E$ ，连接 $B P$ 并延长交对称轴于 $F$ ，证明 $H E + H F$ 的值为定值，并求出这个定值．

查看试题解析