四川省广元市2023年中考三模数学试卷
试卷更新日期:2023-06-19 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、2023 D、-20232. 把图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )
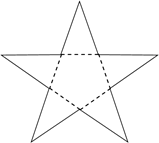 A、五棱锥 B、五棱柱 C、六棱锥 D、六棱柱3. 以下计算正确的是( )A、 B、 C、 D、4. 小红对数据17,26,35,5□,56进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、中位数 B、众数 C、平均数 D、方差5. 我国古代数学名著《九章算术》中记载:“粟米之法:粟率五十;粝米三十.今有米在十斗桶中,不知其数.满中添粟而春之,得米七斗.问故米几何?”意思为:50斗谷子能出30斗米,即出米率为 . 今有米在容量为10斗的桶中,但不知道数量是多少.再向桶中加满谷子,再舂成米,共得米7斗.问原来有米多少斗?如果设原来有米x斗,向桶中加谷子y斗,那么可列方程组为( )A、 B、 C、 D、6. 珠江流域某江段江水流向经过B、C、D三点,拐弯后与原来方向相同,如图,若 , 则等于( )
A、五棱锥 B、五棱柱 C、六棱锥 D、六棱柱3. 以下计算正确的是( )A、 B、 C、 D、4. 小红对数据17,26,35,5□,56进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、中位数 B、众数 C、平均数 D、方差5. 我国古代数学名著《九章算术》中记载:“粟米之法:粟率五十;粝米三十.今有米在十斗桶中,不知其数.满中添粟而春之,得米七斗.问故米几何?”意思为:50斗谷子能出30斗米,即出米率为 . 今有米在容量为10斗的桶中,但不知道数量是多少.再向桶中加满谷子,再舂成米,共得米7斗.问原来有米多少斗?如果设原来有米x斗,向桶中加谷子y斗,那么可列方程组为( )A、 B、 C、 D、6. 珠江流域某江段江水流向经过B、C、D三点,拐弯后与原来方向相同,如图,若 , 则等于( )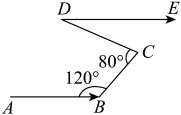 A、50° B、40° C、30° D、20°7. 下列命题正确的是( )A、若分式方程有增根,则它的增根是 B、两边及一角对应相等的两个三角形全等 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、已知抛物线 , 当时,8. 如图,把半径为3的⊙O沿弦AB,AC折叠,使和都经过圆心O,则阴影部分的面积为( ).
A、50° B、40° C、30° D、20°7. 下列命题正确的是( )A、若分式方程有增根,则它的增根是 B、两边及一角对应相等的两个三角形全等 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、已知抛物线 , 当时,8. 如图,把半径为3的⊙O沿弦AB,AC折叠,使和都经过圆心O,则阴影部分的面积为( ).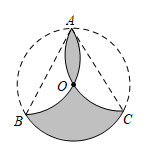 A、 B、 C、 D、9. 如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图像过点C,则k的值为( )
A、 B、 C、 D、9. 如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图像过点C,则k的值为( )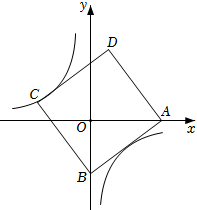 A、4 B、﹣4 C、﹣3 D、310. 如图,已知 , 分别为正方形的边 , 的中点,与交于点.则下列结论:① , ② , ③ , ④.其中正确结论的有( )
A、4 B、﹣4 C、﹣3 D、310. 如图,已知 , 分别为正方形的边 , 的中点,与交于点.则下列结论:① , ② , ③ , ④.其中正确结论的有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
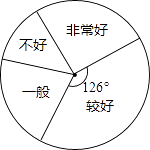
11. 因式分解: .12. 据报道,生命科学家开发出一项突破性的技术,只要把所需要的尺寸输入电脑,就能培养出完全符合要求的肌体组织或骨骼,而所使用的材料每层只有0.0012厘米厚,这个数用科学记数法表示应为厘米.13. 如图,一个质地均匀的正五边形转盘,指针的位置固定,当转盘自由转动停止后,观察指针指向区域内的数(若指针正好指向分界线,重新转一次),这个数是一个奇数的概率是 .
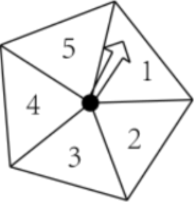 14. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点C,与反比例函数在第一象限内的图象交于点B,连接 . 若 , 则的值是 .
14. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点C,与反比例函数在第一象限内的图象交于点B,连接 . 若 , 则的值是 .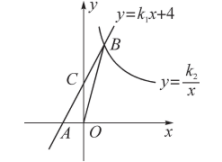 15. 如图,在 中, .利用尺规在 、 上分别截取 、 ,使 ;分别以 、 为圆心,大于 的长为半径作弧,两弧在 内交于点 ;作射线 交 于点 .若 ,则 的长为.
15. 如图,在 中, .利用尺规在 、 上分别截取 、 ,使 ;分别以 、 为圆心,大于 的长为半径作弧,两弧在 内交于点 ;作射线 交 于点 .若 ,则 的长为.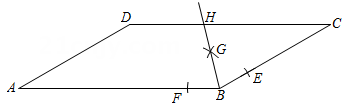 16. 抛物线交x轴于点、 . 下列结论:①;②;③当时,无论m取何值都有;④若时,抛物线交y轴于点C,且是等腰三角形,或;⑤抛物线交y轴于正半轴,抛物线上的两点、且 , , 则;则其中正确的是 . (填写所有正确结论的序号)
16. 抛物线交x轴于点、 . 下列结论:①;②;③当时,无论m取何值都有;④若时,抛物线交y轴于点C,且是等腰三角形,或;⑤抛物线交y轴于正半轴,抛物线上的两点、且 , , 则;则其中正确的是 . (填写所有正确结论的序号)三、解答题
-
17. 计算:18. 先化简,再求值: , 其中x满足方程 .19. 如图,在四边形中, , , 平分 . 过点D作交的延长线于点E.
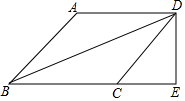 (1)、求证:四边形是菱形;(2)、若 , 四边形的面积为 , 求的长.20. 为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.请根据图表中提供的信息,解答下列问题:
(1)、求证:四边形是菱形;(2)、若 , 四边形的面积为 , 求的长.20. 为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.请根据图表中提供的信息,解答下列问题:整理情况
频数
频率
非常好
0.21
较好
70
一般
不好
36
 (1)、本次抽样共调查了多少学生?(2)、补全统计表中所缺的数据.(3)、该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?(4)、某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.21. 我国首艘国产航母“山东”号是保障国土安全,维护祖国统的又一利器.如图,一架歼15舰载机在航母正后方A点准备降落,此时在A测得航母舰首B的俯角为11.3°,舰尾C的俯角为14°,如果航空母舰长为315米且B比C高出10米,求舰载机相对舰尾C的高度(参考数据:sinl1.3°=0. 22, sin14°=0. 24,tanl1.3°=0.2,tan14° =0.25)
(1)、本次抽样共调查了多少学生?(2)、补全统计表中所缺的数据.(3)、该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?(4)、某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.21. 我国首艘国产航母“山东”号是保障国土安全,维护祖国统的又一利器.如图,一架歼15舰载机在航母正后方A点准备降落,此时在A测得航母舰首B的俯角为11.3°,舰尾C的俯角为14°,如果航空母舰长为315米且B比C高出10米,求舰载机相对舰尾C的高度(参考数据:sinl1.3°=0. 22, sin14°=0. 24,tanl1.3°=0.2,tan14° =0.25)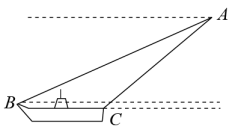 22. 如图,在平面直角坐标系中,直线与反比例函数的图象交于M,N两点(点M在点N左侧),已知M点的纵坐标是2;
22. 如图,在平面直角坐标系中,直线与反比例函数的图象交于M,N两点(点M在点N左侧),已知M点的纵坐标是2;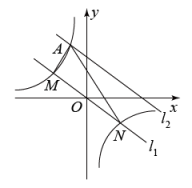 (1)、求反比例函数的表达式;(2)、根据图象直接写出的解集;(3)、将直线沿y轴向上平移后得到直线 , 与反比例函数的图像在第二象限内交于点A,如果的面积为18,求直线的函数表达式.23. 学校开展大课间活动,某班需要购买A、B两种跳绳.已知购进10根A种跳绳和5根B种跳绳共需175元:购进15根A种跳绳和10根B种跳绳共需300元.(1)、求购进一根A种跳绳和一根B种跳绳各需多少元?(2)、设购买A种跳绳m根,若班级计划购买A、B两种跳绳共45根,所花费用不少于548元且不多于560元,则有哪几种购买方案?(3)、在(2)的条件下,哪种购买方案需要的总费用最少?最少费用是多少元?24. 如图,AB为⊙O的直径,D、E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠BAD.
(1)、求反比例函数的表达式;(2)、根据图象直接写出的解集;(3)、将直线沿y轴向上平移后得到直线 , 与反比例函数的图像在第二象限内交于点A,如果的面积为18,求直线的函数表达式.23. 学校开展大课间活动,某班需要购买A、B两种跳绳.已知购进10根A种跳绳和5根B种跳绳共需175元:购进15根A种跳绳和10根B种跳绳共需300元.(1)、求购进一根A种跳绳和一根B种跳绳各需多少元?(2)、设购买A种跳绳m根,若班级计划购买A、B两种跳绳共45根,所花费用不少于548元且不多于560元,则有哪几种购买方案?(3)、在(2)的条件下,哪种购买方案需要的总费用最少?最少费用是多少元?24. 如图,AB为⊙O的直径,D、E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠BAD. (1)、求证:CD是⊙O的切线.(2)、若tan∠BED= , AC=9,求⊙O的半径.25. 如图 在中, , , 将线段绕点逆时针旋转角得到线段 , 连接 , 过点作于点 , 连接交 , 于点F,G.
(1)、求证:CD是⊙O的切线.(2)、若tan∠BED= , AC=9,求⊙O的半径.25. 如图 在中, , , 将线段绕点逆时针旋转角得到线段 , 连接 , 过点作于点 , 连接交 , 于点F,G.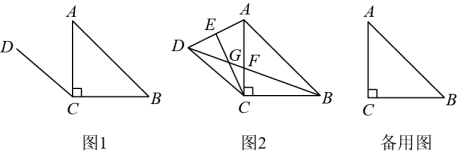 (1)、当时,如图1,依题意补全图形,直接写出的大小;(2)、当时,如图2,试判断线段与之间的数量关系,并证明你的结论;(3)、若F为的中点,直接写出的长.26. 如图,抛物线与轴交于A(-1,0),B(3,0)两点,与y轴交于点C,直线经过B,C两点,连接AC.
(1)、当时,如图1,依题意补全图形,直接写出的大小;(2)、当时,如图2,试判断线段与之间的数量关系,并证明你的结论;(3)、若F为的中点,直接写出的长.26. 如图,抛物线与轴交于A(-1,0),B(3,0)两点,与y轴交于点C,直线经过B,C两点,连接AC.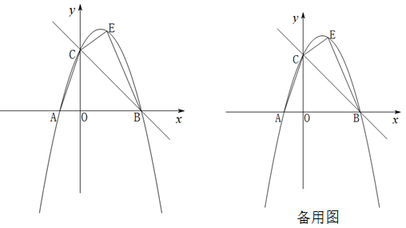 (1)、求抛物线的表达式;(2)、点E为直线BC上方的抛物线上的一动点(点E不与点B,C重合),连接BE,CE,设四边形BECA的面积为S,求S的最大值;(3)、若点Q在轴上,则在抛物线上是否存在一点P,使得以B,C,P,Q四点为顶点的四边形是平行四边形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、点E为直线BC上方的抛物线上的一动点(点E不与点B,C重合),连接BE,CE,设四边形BECA的面积为S,求S的最大值;(3)、若点Q在轴上,则在抛物线上是否存在一点P,使得以B,C,P,Q四点为顶点的四边形是平行四边形?若存在,请直接写出P点的坐标;若不存在,请说明理由.