四川省成都市郫都区2023年中考二模数学试卷
试卷更新日期:2023-06-19 类型:中考模拟
一、单选题
-
1. 两千多年前,中国人就开始使用负数,如果收入100元记作元,那么支出60元应记作( )A、-60元 B、40元 C、+40元 D、+60元2. 如图是由4个大小相同的正方体组合而成的几何体,其左视图是( )
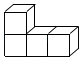 A、
A、 B、
B、 C、
C、 D、
D、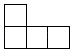 3. 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为4400000000人,这个数用科学记数法表示为( )A、 B、 C、 D、4. 点P(-2,-3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为( )A、(-3,0) B、(-1,6) C、(-3,-6) D、(-1,0)5. 下列计算正确的是( )A、 B、 C、 D、6. 成都是国家历史文化名城,区域内的都江堰、武侯祠、杜甫草堂、金沙遗址、青羊宫都有深厚的文化底蕴,某班同学分小组到以上五个地方进行研学旅行,人数分别为:10,9,11,10,8(单位:人),这组数据的众数和中位数分别是( )A、10人,9人 B、10人,10人 C、10人,11人 D、8人,11人7. 如图,在数轴上表示的不等式组的解集,这个解集为( )
3. 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为4400000000人,这个数用科学记数法表示为( )A、 B、 C、 D、4. 点P(-2,-3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为( )A、(-3,0) B、(-1,6) C、(-3,-6) D、(-1,0)5. 下列计算正确的是( )A、 B、 C、 D、6. 成都是国家历史文化名城,区域内的都江堰、武侯祠、杜甫草堂、金沙遗址、青羊宫都有深厚的文化底蕴,某班同学分小组到以上五个地方进行研学旅行,人数分别为:10,9,11,10,8(单位:人),这组数据的众数和中位数分别是( )A、10人,9人 B、10人,10人 C、10人,11人 D、8人,11人7. 如图,在数轴上表示的不等式组的解集,这个解集为( ) A、 B、 C、或 D、8. 二次函数的图象如图所示,则下列结论中正确的是( )
A、 B、 C、或 D、8. 二次函数的图象如图所示,则下列结论中正确的是( ) A、 B、函数的最小值为 C、当时, D、
A、 B、函数的最小值为 C、当时, D、二、填空题
-
9. 若 , 且 , 则的值为 .10. 如图,平地上的两个小朋友玩跷跷板.已知跳跷板的支点是长板的中点,支柱高1米当长板的一端着地时,长板的另一端到地面的高度为 .
 11. 如果分式 有意义,那么x的取值范围是.12. 一根排水管的截面如图所示,已知排水管的半径OB=5cm,水面宽AB=8,则截面圆心O到水面的距离OC的长是.
11. 如果分式 有意义,那么x的取值范围是.12. 一根排水管的截面如图所示,已知排水管的半径OB=5cm,水面宽AB=8,则截面圆心O到水面的距离OC的长是. 13. 如图,在中,按以下步骤作图:①分别以B,C为圆心,大于的长为半径画弧,两弧相交于M,N两点;②作直线交于点D,连接 . 若 , 则的度数为 .
13. 如图,在中,按以下步骤作图:①分别以B,C为圆心,大于的长为半径画弧,两弧相交于M,N两点;②作直线交于点D,连接 . 若 , 则的度数为 .
三、解答题
-
14.(1)、计算:;(2)、化简: .15. 为了传承优秀传统文化,我校开展“经典诵读”比赛互动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母 , , 依次表示这三个诵读材料),将 , , 这三个字母分别写在张完全相同的不透明卡片的正面上,把这张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
求:
(1)、小明诵读《论语》的概率(2)、小明和小亮诵读两个不同材料的概率.16. 如图,有大树和建筑物 , 从建筑物的顶部处看树顶处的仰角为 , 看树干处的俯角为 . 若在同一水平地面上,已知米,米.求大树的高度(参考数据: , , ).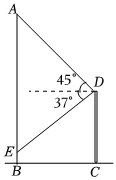 17. 如图,在中, , 点在斜边上,以为圆心,为半径作 , 分别与、相交于点、 , 连接 . 已知 .
17. 如图,在中, , 点在斜边上,以为圆心,为半径作 , 分别与、相交于点、 , 连接 . 已知 . (1)、求证:是的切线;(2)、若 , , 求的长.18. 如图,一次函数的图象与反比例函数的图象相交于、两点(点在点的左侧).
(1)、求证:是的切线;(2)、若 , , 求的长.18. 如图,一次函数的图象与反比例函数的图象相交于、两点(点在点的左侧). (1)、若点的纵坐标为7,求点的坐标;(2)、若时,求反比例函数的表达式;(3)、连接并延长 , 交反比例函数的图象于点 , 连接交轴于点 , 若 , 求的面积.
(1)、若点的纵坐标为7,求点的坐标;(2)、若时,求反比例函数的表达式;(3)、连接并延长 , 交反比例函数的图象于点 , 连接交轴于点 , 若 , 求的面积.四、填空题
-
19. 已知 , 则的值为 .20. 关于的方程有两个实数根,则的取值范围是 .21. 我国的学者墨翟和他的学生做了世界上第一个小孔成倒像的实验,早于牛顿2000多年就已经总结出相似的理论如图,平面 , , 相互平行,平面到平面的距离是平面到平面的距离的2倍,直角三角形光源在平面上,若 , 通过小孔成的像在平面上,则的面积为 .
 22. 定义:若一个函数图象上存在横纵坐标相等的点,则称该点为这个函数图象的“等值点”.例如,点是函数的图象的“等值点”.若函数的图象记为 , 将其沿直线翻折后的图象记为 . 当、两部分组成的图象上恰有2个“等值点”时,的取值范围为 .23. 如图,矩形中, , , 点是的中点,点是边上一动点.将沿着翻折,使得点落在点处,若点是矩形内一动点,连接、、 , 则的最小值为 .
22. 定义:若一个函数图象上存在横纵坐标相等的点,则称该点为这个函数图象的“等值点”.例如,点是函数的图象的“等值点”.若函数的图象记为 , 将其沿直线翻折后的图象记为 . 当、两部分组成的图象上恰有2个“等值点”时,的取值范围为 .23. 如图,矩形中, , , 点是的中点,点是边上一动点.将沿着翻折,使得点落在点处,若点是矩形内一动点,连接、、 , 则的最小值为 .
五、解答题
-
24. 某超市进了一批成本为8元个的文具盒,调查发现:这种文具盒每个星期的销售量(个)与它的定价(元个)的关系如图所示:
 (1)、求这种文具盒每个星期的销售量与它的定价之间的函数关系式;(2)、若该超市每星期销售这种文具盒的销售量不少于125个,且单件利润不低于3元,当每个文具盒定价多少元时,超市每星期利润最高?最高利润是多少?
(1)、求这种文具盒每个星期的销售量与它的定价之间的函数关系式;(2)、若该超市每星期销售这种文具盒的销售量不少于125个,且单件利润不低于3元,当每个文具盒定价多少元时,超市每星期利润最高?最高利润是多少?

