广东省揭西县五校联考2022-2023学年七年级下学期月考数学试题
试卷更新日期:2023-06-19 类型:月考试卷
一、单选题(每小题3分,共10小题,共30分)
-
1. 下列计算中,正确的是( )A、 B、 C、 D、2. 下列各组线段能组成三角形的是( )A、3cm、4cm、5cm B、4cm、6cm、10cm C、3cm、3cm、6cm D、5cm、12cm、18cm3. 某大学芯片研学院研发的某种芯片的厚度约为0.00014米,数据“0.00014”用科学记数法可表示为( )A、 B、 C、 D、4. 如图,在和中, , , 添加下列条件,不能判定的是( )
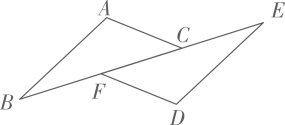 A、 B、 C、 D、5. 下列多项式乘法中,能用平方差公式计算的是( )A、 B、 C、 D、6. 如图,直线 , 相交于点 , , 平分 , , 则的度数是( )
A、 B、 C、 D、5. 下列多项式乘法中,能用平方差公式计算的是( )A、 B、 C、 D、6. 如图,直线 , 相交于点 , , 平分 , , 则的度数是( ) A、 B、 C、 D、7. 如图,是上一点,交于点 , , , , , 则的长度为( )
A、 B、 C、 D、7. 如图,是上一点,交于点 , , , , , 则的长度为( ) A、2 B、2.5 C、4 D、58. 在1000米中长跑考试中,小明开始慢慢加速,当达到某一速度后保持匀速,最后200米时奋力冲刺跑完全程,下列最符合小明跑步时的速度y(单位:米/分)与时间x(单位:分)之间的大致图象的是( )A、
A、2 B、2.5 C、4 D、58. 在1000米中长跑考试中,小明开始慢慢加速,当达到某一速度后保持匀速,最后200米时奋力冲刺跑完全程,下列最符合小明跑步时的速度y(单位:米/分)与时间x(单位:分)之间的大致图象的是( )A、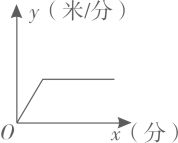 B、
B、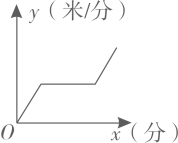 C、
C、 D、
D、 9. 如图是一款手推车的平面示意图,其中 , , , 则的度数为( )度.
9. 如图是一款手推车的平面示意图,其中 , , , 则的度数为( )度. A、56 B、66 C、98 D、10410. 一副三角板按如图所示叠放在一起,其中点、重合,若固定三龟板 , 三角板绕点在平面内旋转,当( )时, .
A、56 B、66 C、98 D、10410. 一副三角板按如图所示叠放在一起,其中点、重合,若固定三龟板 , 三角板绕点在平面内旋转,当( )时, .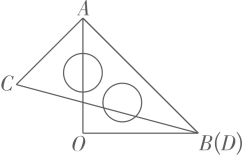 A、 B、或 C、或 D、或
A、 B、或 C、或 D、或二、填空题(每小题3分,共5小题,共15分)
-
11. 计算: .12. 一个角的余角是 , 那么这个角的补角是 .13. 已知 , , 则 .14. 任意给一个非零数 , 按下列程序写出输出结果:(写出与的关系式) .15. 如图,在中,点是的中点,连接 , 点在上,且 , 于点 . 若 , , 则的面积为 .

三、解答题(一)(每小题8分,共3小题,共24分)
-
16. 先化简,再求值: , 其中 , .17. 作图题(要求:用尺规作图,不写作法,保留作图痕迹).
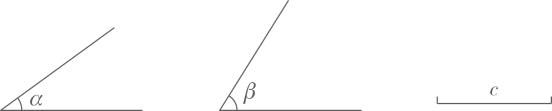
已知: , , 线段 .
求作: , 便 , , .
 18. 已知:如图 , 分别交、于点、 , 平分 , 平分 . 试说明: .
18. 已知:如图 , 分别交、于点、 , 平分 , 平分 . 试说明: .
四、解答题(二)(每小题9分,共3小题,共27分)
-
19. 如图,点、、、在直线上(、之间不能直接测量),点、在㫒侧,测得 , , .
 (1)、试说明:;(2)、若 , , 求的长度.20. 为了加强居民的节水意识,合理利用水资源,某高档小区对直饮水采用价格调控手段以期待达到节水的目的,如图是此小区对居民直饮水某月用水量吨与水费元的关系的图象(水费按月结算).
(1)、试说明:;(2)、若 , , 求的长度.20. 为了加强居民的节水意识,合理利用水资源,某高档小区对直饮水采用价格调控手段以期待达到节水的目的,如图是此小区对居民直饮水某月用水量吨与水费元的关系的图象(水费按月结算). (1)、填空:
(1)、填空:价格表
每月用水量
单价
不超出6吨的部分
元/吨
超出6吨不超出10吨的部分
元/吨
超出10吨的部分
元/吨
(2)、若某户居民9月份用水量为9.5时,求该用户9月份水费;(3)、若某户居民11月用水(吨)(),用含的代数式表示该户居民11月共应交水费(元).21. 已知的三边长是 , , .(1)、若 , , 且三角形的周长是小于18的偶数.求边的长;(2)、化简 .五、解答题(三)(每小题12分,共2小题,共24分)
-
22. 我们已经知道,通过计算几何图形的面积可以表示一些代数垣等式.例如图1可以得到 , 基于此,请解答下列问题:
 (1)、若 , , 则;(2)、若 , 则;(3)、两块完全相同的特制直角三角板如图2所示放置,其中 , , 在一直线上,连接 , , 若 , , 求一块特制三角板的面积.23. 已知材料1:三个内角相等的三角形为等边三角形.
(1)、若 , , 则;(2)、若 , 则;(3)、两块完全相同的特制直角三角板如图2所示放置,其中 , , 在一直线上,连接 , , 若 , , 求一块特制三角板的面积.23. 已知材料1:三个内角相等的三角形为等边三角形.材料2:在同一个三角形中,大角对大边,小角对小边.
结合上述材料,解决下面的问题
如图, , , . 点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动.它们运动的时间为 .
 (1)、若点的运动速度与点的运动速度相等,当时,与的大小关系是;的度数是 .(2)、当时,设点的运动速度为 , 是否存在实数 , 使得与全等?若存在,求出相应的 , 的值;若不存在,请说明理由.
(1)、若点的运动速度与点的运动速度相等,当时,与的大小关系是;的度数是 .(2)、当时,设点的运动速度为 , 是否存在实数 , 使得与全等?若存在,求出相应的 , 的值;若不存在,请说明理由.