云南省昭通市永善县2023年中考二模数学试卷

试卷更新日期：2023-06-19 类型：中考模拟

进入出卷网下载

一、单选题

1. 国家统计局2021年5月11日公布了第七次全国人口普查结果，全国总人口约14.1亿人，将14.1亿用科学记数法表示为（）

A、14.1×10⁸ B、1.41×10⁸ C、1.41×10⁹ D、0.141×10¹⁰

查看试题解析
2. 如图， $∠ 1 = 120 °$ ，要使 $a // b$ ，则 $∠ 2$ 的大小是（）

A、 $60 °$ B、 $80 °$ C、 $100 °$ D、 $120 °$

查看试题解析
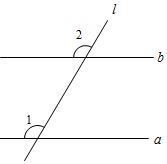3. 遵义市2019年6月1日的最高气温是25℃，最低气温是15℃，遵义市这一天的最高气温比最低气温高（）

A、25℃ B、15℃ C、10℃ D、﹣10℃

查看试题解析
4. 函数 y＝ $\frac{a}{x}$ 和一次函数 y＝－ax＋1(a≠0)在同一平面直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
5. 如图， $△ A B C$ 中， $C E$ 交 $A B$ 于点 $D$ ， $∠ A = ∠ E$ ， $A D ： D B = 2 ： 3$ ， $A B = 10$ ， $E D = 5$ ，则 $D C$ 的长等于（）

A、 $\frac{24}{5}$ B、 $\frac{6}{5}$ C、 $\frac{10}{3}$ D、 $\frac{15}{2}$

查看试题解析
6. 在2023年“五四青年节”来临之际，实验中学开展“我的青春，我的梦”演讲比赛中，五名选手的成绩及部分统计信息如表：
组员及项目
甲
乙
丙
丁
戊
方差
平均成绩
得分
91
89
□
92
90
□
90
其中被遮住的两个数据依次是（）

A、88， $\sqrt{2}$ B、88，2 C、90， $\sqrt{2}$ D、90，2

查看试题解析
7. 下列几何体中，哪一个几何体的三视图完全相同（）

A、 B、 C、 D、

查看试题解析
8. 关于x的分式方程 $\frac{a x - 3}{x - 2} + 1 = \frac{3 x - 1}{2 - x}$ 的解为正数，且使关于y的一元一次不等式组 ${\begin{array}{l} \frac{3 y - 2}{2} \leq y - 1 \\ y + 2 > a \end{array}$ 有解，则所有满足条件的整数a的值之和是（）

A、 $- 5$ B、 $- 4$ C、 $- 3$ D、 $- 2$

查看试题解析
9. 如图， $A C = B C$ ， $A D = B D$ ，这个图形叫做“筝形”，数学兴趣小组几名同学探究出关于它的如下结论：① $△ A C D ≌ △ B C D$ ；② $A O = B O$ ；③ $A B ⊥ C D$ ；④ $∠ C A B = ∠ A B D$ ．其中正确结论的序号是（）

A、①②③④ B、①②③ C、①②④ D、②③④

查看试题解析
10. 下列计算正确的是（）

A、 $a^{2} + 2 a^{2} = 3 a^{4}$ B、 $a^{6} \div a^{3} = a^{2}$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 ${(a b)}^{2} = a^{2} b^{2}$

查看试题解析
11. 观察下列等式：
$3^{1} = 3$ ， $3^{2} = 9$ ， $3^{3} = 27$ ， $3^{4} = 81$ ， $3^{5} = 243$ ， …，
根据其中的规律可得 $3^{1} + 3^{2} + 3^{3} + \dots + 3^{2023}$ 的结果的个位数字是（）

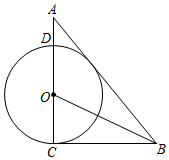
A、0 B、2 C、7 D、9

查看试题解析
12. 如图，以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点，交直角边AC于点E；B、E是半圆弧的三等分点， $\overset{⌢}{B D}$ 的长为 $\frac{4 π}{3}$ ，则图中阴影部分的面积为（）

A、 $6 \sqrt{3} - \frac{4 π}{3}$ B、 $9 \sqrt{3} - \frac{8 π}{3}$ C、 $\frac{3 \sqrt{3}}{2} - \frac{2 π}{3}$ D、 $6 \sqrt{3} - \frac{8 π}{3}$

查看试题解析

二、填空题

13. 已知 $x^{2} - 2 \sqrt{3} x + 1 = 0$ ，则 $x - \frac{1}{x} =$ .

查看试题解析
14. 如图，在底边BC为2 $\sqrt{3}$ ，腰AB为2的等腰三角形ABC中，DE垂直平分AB于点D，交BC于点E，则 $△ A C E$ 的周长.

查看试题解析
15. 如图，点E为矩形ABCD的边BC长上的一点，作DF⊥AE于点F，且满足DF＝AB．下面结论：①△DEF≌△DEC；②S_△ABE = S_△ADF；③AF＝AB；④BE＝AF．其中正确的结论是．

查看试题解析
16. 如下图，正方形ABCD的边AB在x轴上，A（﹣4，0），B（﹣2，0），定义：若某个抛物线上存在一点P，使得点P到正方形ABCD四个顶点的距离相等，则称这个抛物线为正方形ABCD的“友好抛物线”．若抛物线y=2x²﹣nx﹣n²﹣1是正方形ABCD的“友好抛物线”，则n的值为．

查看试题解析

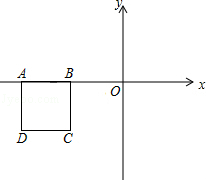
三、解答题

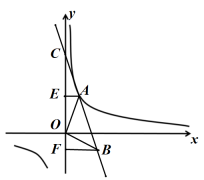
17. 先化简，再求值： $(\frac{2 x^{2} + 2 x}{x^{2} - 1} - \frac{x^{2} - x}{x^{2} - 2 x + 1}) \div \frac{x}{x + 1}$ ，其中 $x = | \sqrt{3} - 2 | + {(\frac{1}{2})}^{- 1} - {(π - 3.14)}^{0} - \sqrt[3]{27} + 1$ ．

查看试题解析
18. 如图，在平面直角坐标系中，点 $A 、 B 、 C$ 的坐标分别为 $(- 1 ， 3)$ 、 $(- 4 ， 1)$ 、 $(- 2 ， 1)$ ，

(1)、作出与 $△ A B C$ 关于 $x$ 轴对称的 $△ A_{1} B_{1} C_{1}$ ， $A_{1}$ 的坐标为 ▲ ；

(2)、再将 $△ A_{1} B_{1} C_{1}$ 绕点 $A_{1}$ 顺时针旋转 $9 0^{∘}$ 得到 $△ A_{1} B_{2} C_{2}$ 画出 $△ A_{1} B_{2} C_{2}$ ；

(3)、求出在（2）的变换过程中，点 $B_{1}$ 到达点 $B_{2}$ 走过的路径长

查看试题解析

19. 为了解学生掌握垃圾分类知识的情况，增强学生环保意识，某学校举行了“垃圾分类人人有责”的知识测试活动，现从该校七，八年级中各随机抽取20名学生的测试成绩（满分10分，6分及6分以上为合格）进行整理、描述和分析，下面给出了部分信息．

七年级20名学生的测试成绩为：

7，8，7，9，7，6，5，9，10，9，8，5，8，7，6，7，9，7，10，6．

七，八年级抽取的学生的测试成绩的平均数、众数、中位数、8分及以上人数所占百分比如下表所示：

年级	平均数	众数	中位数	8分及以上人数所占百分比
七年级	7.5	a	7	45%
八年级	7.5	8	b	c

八年级20名学生的测试成绩条形统计图如图：

根据以上信息，解答下列问题：

(1)、直接写出上述表中的a，b，c的值；

(2)、根据以上数据，你认为该校七，八年级中哪个年级学生掌握垃圾分类知识较好？请说明理由（写出一条理由即可）；

(3)、该校七，八年级共1200名学生参加了此次测试活动，估计参加此次测试活动成绩合格的学生人数是多少？

查看试题解析

20. 如果一个两位正整数，某个位数字大于十位数字，则称这个两位数为“两位递增数”（如14，56，37）．在一次趣味数学活动中，参加者需从分别写有数字1，2，3，4，5的5张卡片中随机抽取两张，组成一个“两位递增数”

(1)、写出所有个位数字是4的“两位递增数”：；

(2)、请用列表法或树状图，求组成的“两位递增数”刚好是2的倍数的概率．

查看试题解析
21. 如图，在四边形ABCD中，点E和点F是对角线AC上的两点，AE＝CF，DF＝BE，且DF∥BE，过点C作CG⊥AB交AB的延长线于点G.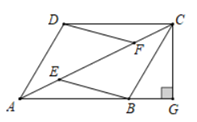

(1)、求证：四边形ABCD是平行四边形；

(2)、若tan∠CAB＝ $\frac{2}{5}$ ，∠CBG＝45°，BC＝4 $\sqrt{2}$ ，则▱ABCD的面积是.

查看试题解析
22. 某学校为改善办学条件，计划采购A、B两种型号的空调，已知采购3台A型空调和2台B型空调，需费用39000元；4台A型空调比5台B型空调的费用多6000元．

(1)、求A型空调和B型空调每台各需多少元；

(2)、若学校计划采购A、B两种型号空调共30台，且A型空调的台数不少于B型空调的一半，两种型号空调的采购总费用不超过217000元，该校共有哪几种采购方案？

(3)、在（2）的条件下，采用哪一种采购方案可使总费用最低，最低费用是多少元？

查看试题解析
23. 如图，△ABC中，∠ACB＝90°，BO为△ABC的角平分线，以点O为圆心，OC为半径作⊙O与线段AC交于点D.

(1)、求证：AB为⊙O的切线；

(2)、若tanA＝ $\frac{3}{4}$ ，AD＝2，求BO的长.

查看试题解析
24. 如图所示， $△ O A B$ 的顶点A在反比例函数 $y = \frac{k}{x} (k > 0)$ 的图像上，直线AB交y轴于点C，且点C的纵坐标为5，过点A、B分别作y轴的垂线AE、BF，垂足分别为点E、F，且 $A E = 1$ ．

(1)、若点E为线段OC的中点，求k的值；

(2)、若 $△ O A B$ 为等腰直角三角形， $∠ A O B = 90 °$ ，其面积小于3．
①求证： $△ O A E ≌ △ B O F$ ；

②把 $| x_{1} - x_{2} | + | y_{1} - y_{2} |$ 称为 $M (x_{1} ， y_{1})$ ， $N (x_{2} ， y_{2})$ 两点间的“ZJ距离”，记为 $d (M ， N)$ ，求 $d (A ， C) + d (A ， B)$ 的值．

查看试题解析

组员及项目	甲	乙	丙	丁	戊	方差	平均成绩
得分	91	89	□	92	90	□	90