云南省西双版纳傣族自治州景洪市2023年中考一模数学试题

试卷更新日期：2023-06-19 类型：中考模拟

进入出卷网下载

一、单选题

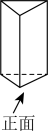
1. 两个数表示的意义相反，则分别叫做正数与负数．已知气温零上5℃记作 $+ 5$ ℃，则 $- 3$ ℃表示（）．

A、零上3℃ B、零下3℃ C、零上7℃ D、零下7℃

查看试题解析
2. 如图所示几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算结果为 $a^{5}$ 的是（）

A、 $a^{6} - a$ B、 $a^{2} \cdot a^{3}$ C、 $a^{10} \div a^{2}$ D、 ${(a^{2})}^{3}$

查看试题解析
4. 如图，D，E分别是△ABC的边AB，AC上的中点，如果△ADE的周长是6，则△ABC的周长是（）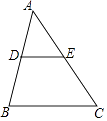

A、6 B、12 C、18 D、24

查看试题解析
5. 下列计算，正确的是（）

A、（ $\frac{1}{2}$ ）^-¹＝2 B、| $\frac{1}{2} - 2$ |＝- $\frac{3}{2}$ C、 $\sqrt[3]{8} = 2 \sqrt{2}$ D、 $\sqrt{8} - \sqrt{2} = \sqrt{6}$

查看试题解析
6. 若一个多边形的每一个外角都是40°，则这个多边形是(　　)

A、七边形 B、八边形 C、九边形 D、十边形

查看试题解析
7. 函数y= $\sqrt{1 - x}$ 的自变量x的取值范围为（）

A、x≤0 B、x≤1 C、x≥0 D、x≥1

查看试题解析
8. 如图，在矩形ABCD中，点E在DC上，将矩形沿AE折叠，使点D落在BC边上的点F处，若 $A B = 3$ ， $B C = 5$ ，则 $t a n ∠ F E C$ 的值为（）．

A、 $\frac{1}{2}$ B、 $\frac{3}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{5}$

查看试题解析
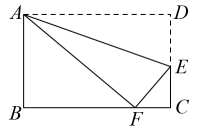9. 按照一定规律排列的数： $- 2$ ， 4， $- 8$ ， 16， $- 32$ ， 64，…，第n个数为（）．

A、 ${(- 1)}^{2} \cdot n^{2}$ B、 ${(- 1)}^{n} \cdot 2 n$ C、 ${(- 1)}^{n + 1} \cdot 2^{n}$ D、 ${(- 1)}^{n} \cdot 2^{n}$

查看试题解析
10. 相关部门对“五一”期间到某景点观光的游客的出行方式进行了随机抽样调查，整理绘制了两幅尚不完整的统计图，根据图中信息，下列结论不正确的是（）．

A、本次抽样调查的样本容量是500 B、扇形统计图中“其它”的占比为10％ C、样本中选择公共交通出行的有250人 D、若“五一”期间到该景点观光的游客有50万人，则选择自驾出行的约有25万人

查看试题解析
11. 如图是一个圆锥形冰淇淋外壳，已知其母线长为10cm，底面半径为3cm，则这个冰淇淋外壳的侧面展开图的圆心角度数为（）．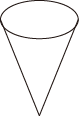

A、108° B、120° C、144° D、150°

查看试题解析
12. 关于 $x$ 的不等式 $2 x + a \leq 1$ 只有2个正整数解，则 $a$ 的取值范围为（）

A、 $- 5 < a < - 3$ B、 $- 5 \leq a < - 3$ C、 $- 5 < a \leq - 3$ D、 $- 5 \leq a \leq - 3$

查看试题解析

二、填空题

13. 分解因式： $a^{3} - 16 a$ ＝

查看试题解析
14. 如图， $A D ∥ B C$ ， BD平分∠ABC，若∠ADB=33°，那么∠A的度数是

查看试题解析
15. 若二次函数y＝2x²－x＋k的图象与x轴有两个公共点，则k的取值范围是．

查看试题解析
16. 如图，已知 $⊙ O$ 是 $△ A B C$ 的内切圆， $∠ A C B = 90 °$ ， BO的延长线交AC于点D，若 $B C = 4$ ， $C D = 1$ ，则 $⊙ O$ 的半径长为．

查看试题解析
17. 若关于x的分式方程 $\frac{2 x}{x - 3} - 1 = \frac{m}{3 - x}$ 有增根，则m的值为．

查看试题解析
18. 在矩形 $A B C D$ 中， $A B = 12 ， B C = 7 ，$ 点E在 $C D$ 边上，点F在 $A B$ 边上，连接 $E F 、 D F ，$ 若 $C E = 3 D E$ ， $E F = 5 \sqrt{2}$ ，则 $D F$ 的长为．

查看试题解析

三、解答题

19. 2022年2月8日，中国选手谷爱凌在冬奥会自由式滑雪女子大跳台决赛中夺得金牌，国际滑联评价谷爱凌为滑雪史上第一人．已知自由式滑雪大跳台的计分规则如下：
①每次滑雪的动作，按照其完成难度的不同对应一个难度系数A；
②每次滑雪都有7名裁判进行打分，在7个得分中去掉1个最高分和1个最低分，剩下5个得分的平均值为这次起跳的完成分B；
③运动员该次滑雪的最后得分C＝难度系数A×完成分B×3．
在某次自由滑雪大跳台比赛中，某运动员的打分（满分10分）表为：
难度系数
裁判
1
2
3
4
5
6
7
3.0
打分
10
9.5
9
9
9.5
9
9

(1)、7名裁判打分的众数是；中位数是；

(2)、该运动员的最后得分是多少？

(3)、已知某运动员在一次滑雪大跳台比赛中完成了难度系数3.2的动作，且所有裁判都打了满分，请你帮她算一下，难度系数3.2的满分成绩应该是多少分？

查看试题解析
20. 小明与小刚做游戏，在甲、乙两个不透明的口袋中，分别装有完全一样的小球，其中甲口袋中的4个小球上分别标有数字1，2，3，4，乙口袋中的3个小球分别标有数字2，3，4，小明先从甲袋中随意摸出一个小球，记下数字为x，再从乙袋中随机摸出一个小球，记下数字为y．

(1)、请用列表或画树状图的方法表示出所有可能出现的结果；

(2)、若x，y都是方程 $x^{2} - 5 x + 6 = 0$ 的解时，则小明获胜；若x，y都不是方程 $x^{2} - 5 x + 6 = 0$ 的解时，则小刚获胜，它们谁获胜的概率大？请说明理由．

查看试题解析
21. 已知：如图，在平行四边形 $A B C D$ 中， $∠ A B C$ 的平分线交 $A D$ 于点 $E$ ，过点 $A$ 作 $B E$ 的垂线交 $B E$ 于点 $F$ ，交 $B C$ 于点 $G$ ，连接 $E G$ 、 $C F$ ，

(1)、求证：四边形 $A B G E$ 是菱形；

(2)、若 $∠ A B C = 60 °$ ， $A B = 4$ ， $A D = 5$ ，则 $C F$ 的长为．

查看试题解析
22. 随着新一轮新冠疫情的爆发，某网店销售的消毒洗手液很畅销．已知该消毒洗手液的运营成本为每瓶4元，市场调查发现，每天的洗手液销售量y（瓶）与销售单价x（元/瓶）（ $6 \leq x \leq 15$ ，且x是正整数）之间满足某种函数关系，下表记录的是部分销售数据：
x（元/瓶）
7
8
9
10
y（瓶）
85
80
75
70

(1)、求出y与x之间的函数关系式；

(2)、设销售这种洗手液每天的利润为W元，求该网店每天销售洗手液的最大利润；

(3)、为了抗击疫情，该网店决定每销售1瓶洗手液便向隔离防控区捐款a元，实施决策后发现，网店每天的利润依然随着售价的增大而增大，则a的最小值是．

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ，以AB为直径作 $⊙ O$ ，交AC边于点D，E是BC的中点，连接DE并延长交AB延长线于点F．

(1)、求证：DF是 $⊙ O$ 的切线：

(2)、若 $A B = 2 B F$ ， $E F = 4$ ，求图中阴影部分的面积．

查看试题解析
24. 已知点 $A (a ， m a + 2)$ 、 $B (b ， m b + 2)$ 是反比例函数 $y = \frac{k}{x}$ 图象上的两个点，且 $a > 0$ ， $b < 0$ ， $m > 0$ ．

(1)、求证： $a + b = - \frac{2}{m}$ ；

(2)、若 $O A^{2} + O B^{2} = 2 a^{2} + 2 b^{2}$ ，求 $m$ 的值；

(3)、若 $S_{△ O A B} = 3 S_{△ O C D} = 3$ ，求 $k m$ 的值．

查看试题解析

难度系数	裁判	1	2	3	4	5	6	7
3.0	打分	10	9.5	9	9	9.5	9	9

x（元/瓶）	7	8	9	10
y（瓶）	85	80	75	70