云南省文山州2023年中考二模数学试卷

试卷更新日期：2023-06-19 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{1}{2}$ 的相反数是（）

A、 $- 2$ B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 如图是某几何体的主视图、左视图和俯视图，则该几何体是（）

A、球体 B、圆锥 C、圆柱 D、三棱锥

查看试题解析
3. 在式子 $\frac{1}{\sqrt{x - 2}}$ 中，x的取值范围是（）

A、 $x > 2$ B、 $x \neq 2$ C、 $x \geq 2$ D、 $x \leq 2$

查看试题解析
4. 如图， $A B ∥ C D$ ，点E在 $A B$ 上， $E C$ 平分 $∠ A E D$ ，若 $∠ 2 = 50 °$ ，则 $∠ 1$ 的度数为（）

A、45° B、50° C、65° D、80°

查看试题解析
5. 预计到2025年，中国5G用户将超过460000000，将460000000用科学记数法表示为（）

A、4.6×10⁹ B、46×10⁷ C、4.6×10⁸ D、0.46×10⁹

查看试题解析
6. 已知一个多边形的内角和等于900º，则这个多边形是（）

A、五边形 B、六边形 C、七边形 D、八边形

查看试题解析
7. 对于反比例函数 $y = \frac{2}{x}$ ，下列说法不正确的是（）

A、图象关于原点成中心对称 B、经过点 $(1 ， 2)$ C、图象位于第一、三象限 D、当 $x > 0$ 时，y随x的增大而增大

查看试题解析
8. 小明作点 $A (1 ， 2)$ 关于x轴的对称点 $A_{1}$ ，再作 $A_{1}$ 关于y轴的对称点 $A_{2}$ ，则 $A_{2}$ 的坐标为（）

A、 $(1 ， 2)$ B、 $(- 1 ， - 2)$ C、 $(- 1 ， 2)$ D、 $(1 ， - 2)$

查看试题解析
9. 下列说法中，正确的是（）

A、为了解某市中学生的睡眠情况适宜采用全面调查 B、一组数据2，5，5，7，7，4，6的中位数是7 C、明天的降水的概率为90%，则明天下雨是必然事件 D、若平均数相同的甲、乙两组数据， ${S_{甲}}^{2} = 0.3$ ， ${S_{乙}}^{2} = 0.02$ ，则乙组数据更稳定

查看试题解析
10. 按一定规律排列的单项式：a， $- 4 a^{2}$ ， $9 a^{3}$ ， $- 16 a^{4}$ ， $25 a^{5}$ ， $- 36 a^{6}$ ， ……，则第n个单项式为（）

A、 $(- 1)^{n} (n + 1)^{2} a^{n}$ B、 $(- 1)^{n + 1} n^{2} a$ C、 $(- 1)^{n + 1} (n + 1)^{2} a^{n}$ D、 $(- 1)^{n + 1} n^{2} a^{n}$

查看试题解析
11. 大约在两千四五百年前，墨子和他的学生做了世界上第1个小孔成倒像的实验．并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”．如图所示的小孔成像实验中，若物距为 $10 c m$ ，像距为 $15 c m$ ，蜡烛火焰倒立的像的高度是 $8 c m$ ，则蜡烛火焰的高度是（）

A、 $\frac{9}{2}$ B、6 C、 $\frac{16}{3}$ D、8

查看试题解析
12. 若干名学生一起去种树，如果每人种4棵，则还剩下3棵树苗；如果每人种植5棵，则缺少5棵树苗．设学生有x人，树苗有y棵，根据题意可列方程组为（）

A、 ${\begin{array}{l} 4 x = y - 3 \\ 5 x = y + 5 \end{array}$ B、 ${\begin{array}{l} 4 x = y + 3 \\ 5 x = y - 5 \end{array}$ C、 ${\begin{array}{l} 4 x = y - 3 \\ 5 x = y - 5 \end{array}$ D、 ${\begin{array}{l} 4 x = y + 3 \\ 5 x = y + 5 \end{array}$

查看试题解析

二、填空题

13. 因式分解： $4 a^{2} - 4 =$ ．

查看试题解析
14. 在等腰 $△ A B C$ 中， $∠ B = 30 °$ ，延长 $B A$ 至点D，则 $∠ C A D$ 的度数为．

查看试题解析
15. 关于x的一元二次方程 $k x^{2} + 2 x - 1 = 0$ 有两个不相等的实数根，则k的最小整数是．

查看试题解析
16. 用纸板制作了一个圆锥模型，它的底面半径为1，高为 $2 \sqrt{2}$ ，则这个圆锥的侧面积为．

查看试题解析

三、解答题

17. 计算： ${(\frac{1}{2})}^{- 1} - 2 s i n 60 ° + {(π - 3)}^{0} + | 1 - \sqrt{3} |$ ．

查看试题解析
18. 如图， $A B = A C$ ， $∠ B A D = ∠ C A E$ ， $∠ B = ∠ C$ ，求证： $A D = A E$ ．

查看试题解析
19. 2023年文山州州庆与清明节、“三月三”民族节假期相近，共放假6天．假日期间，州庆组委会举办了一次隆重、节俭、务实、开放、特色安全的庆祝晚会，晚会的其中一个主题为《欢乐文山行—我为文山代言》，充分展示了文山州独特的民族风情与文化底蕴．某校为了增强学生对文山州特色风情与文化历史的了解，举办了一次文山特色知识竞赛．竞赛结束后发现所有参赛学生的成绩均不低于50分，为了更好地了解本次竞赛的成绩分布情况，校委会随机抽取了其中100名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，得到如下两幅不完整的统计图表：
成绩x/分
频数
频率
$50 \leq x < 60$
5
0.05
$60 \leq x < 70$
10
0.10
$70 \leq x < 80$
a
0.15
$80 \leq x < 90$
30
b
$90 \leq x \leq 100$
40
0.40

请根据所给的信息，解答下列问题：

(1)、 $a =$ ； $b =$ ；

(2)、请补全频数分布直分图；

(3)、若成绩在80分以上（包括80分）的为“优”等，估计该校参加这次竞赛的2000名学生中成绩“优”等的有多少人？

查看试题解析
20. 随着中国传统节日“端午节”的临近，某商场决定开展“欢度端午，回馈顾客”的让利促销活动，在商场大厅设置了如图所示的两个可以自由转动的转盘，在端午节当天消费的顾客可以参与转盘活动．已知这两个转盘都被平均分成了3份，并在每份内均标有数字．规则如下：
①分别转动转盘A、B；

②两个转盘停止后，将两个指针所指区域内的数字相乘（若指针停止在等份线上，那么重转一次，直到指针指向某一区域为止），若数字之积为3的倍数则可以领取3枚粽子；若数字之积为5的倍数则可以领取5枚粽子．

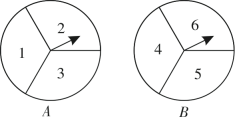(1)、用列表或画树状图的方法表示出所有可能出现的结果；

(2)、在端午节当天，李老师参与了转盘活动，求李老师领取到5枚粽子的概率．

查看试题解析
21. 如图，在 $△ A B C$ 中， $C D$ 平分 $∠ A C B$ ， $C D$ 的垂直平分线分别交 $A C$ 、 $D C$ 、 $B C$ 于点E、F、G，连接 $D E$ 、 $D G$ ．

(1)、求证：四边形 $C E D G$ 是菱形；

(2)、若 $∠ B = 45 °$ ， $t a n ∠ A C B = \frac{1}{2}$ ， $D E = \sqrt{5}$ ，求 $B G$ 的长．

查看试题解析
22. 某中学开展了关于“构建书香校园”的读书活动，以建设书香校园、和谐校园为目标，引领广大师生“走进五千年文明，品读祖国经典文章”．学校计划采购两类图书，通过市场了解到每套A类图书的价格是每套B类图书价格的1.5倍，用4000元购买的B类图书比用3000元购买的A类图书多20套．

(1)、A、B两类图书每套分别是多少元？

(2)、现学校计划采购60套图书，且A类图书的数量不低于B类图书数量的一半，该校应该如何采购两类图书才能使得总费用最低，并求出最低费用．

查看试题解析
23. 如图，A、B、C、D在 $⊙ O$ 上，点D是 $\overset{⌢}{A B}$ 的中点，连接 $A B$ 、 $A C$ 、 $B C$ 、 $C D$ ，过点D作 $D E ∥ A B$ 交 $C B$ 延长线于点E．

(1)、求证： $D E$ 是 $⊙ O$ 的切线；

(2)、点P是弦 $A B$ 下方圆上的一个动点，连接 $A P$ 和 $B P$ ，过点D作 $D H ⊥ B P$ 于点H，点P在运动过程中， $\frac{B H}{A P + B P}$ 的比值是否改变，若改变，请说明理由；若不变，求出这个比值．

查看试题解析
24. 在平面直角坐标系 $x O y$ 中，已知点 $(m ， y_{1})$ 与点 $(- m + 2 ， y_{2})$ ，是抛物线 $y = x^{2} + b x - 2$ 上不同的两个点，且 $y_{1} = y_{2}$ ．

(1)、求抛物线的解析式；

(2)、将抛物线向左平移1个单位长度，再向上平移3个单位长度得到一个新的抛物线，已知A、B两点在新抛物线上，直线 $A B$ ： $y = k x + n$ 恒过点 $(0 ， 1)$ ，设直线 $O A$ ： $y = k_{A} x$ ，直线 $O B$ ： $y = k_{B} x$ ，求 $k_{A} k_{B}$ 的值，并判断 $△ A O B$ 的形状．

查看试题解析

成绩x/分	频数	频率
$50 \leq x < 60$	5	0.05
$60 \leq x < 70$	10	0.10
$70 \leq x < 80$	a	0.15
$80 \leq x < 90$	30	b
$90 \leq x \leq 100$	40	0.40