云南省临沧市凤庆县2023年中考二模数学试卷

试卷更新日期：2023-06-19 类型：中考模拟

进入出卷网下载

一、单选题

1. 学校组建一批身高175cm左右的仪仗队员，将身高177cm记为+2，若某同学身高记为-1，则这名同学的身高是（）

A、173cm B、174cm C、175cm D、176cm

查看试题解析
2. 2022年，中央、省、市、县四级财政衔接推进乡村振兴补助资金总量达3700多亿元.3700亿用科学记数法表示为（）

A、 $3.7 \times 1 0^{11}$ B、 $3.7 \times 1 0^{10}$ C、 $3.7 \times 1 0^{9}$ D、 $3.7 \times 1 0^{8}$

查看试题解析
3. 下列运算中，正确的是（）

A、 ${(- 2 a^{2})}^{3} = - 6 a^{6}$ B、 $3 a b - a b = 2$ C、 ${(2 a - b)}^{2} = 4 a^{2} - b^{2}$ D、 $3 a b \cdot 2 b = 6 a b^{2}$

查看试题解析
4. 如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（）

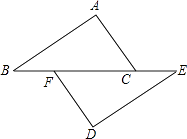A、AB=DE B、AC=DF C、∠A=∠D D、BF=EC

查看试题解析
5. 一直尺与一直角三角板按如图所示方式摆放，若 $∠ 1 = 32 °$ ，则 $∠ 2$ 的度数是（）

A、 $32 °$ B、 $58 °$ C、 $64 °$ D、 $48 °$

查看试题解析
6. 若一次函数 $y = 2 x - 5$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象交于点 $(1 ， m)$ ，则k的值为（）

A、 $- 3$ B、 $- \frac{1}{3}$ C、 $\frac{1}{3}$ D、3

查看试题解析
7. 某几何体的三视图如图所示，该几何体的母线长是（）

A、5 B、10 C、12 D、13

查看试题解析
8. 如图，平行四边形 $A B C D$ 的对角线 $A C ， B D$ 交于点O，E是 $B C$ 的中点，连接 $O E$ ．若 $△ B O E$ 的面积是2，则四边形 $O E C D$ 的面积是（）

A、5 B、6 C、7 D、8

查看试题解析
9. 春节期间，全国大量游客都选择到云南景区旅游．某旅行社为了整合资源，在网络上进行“春节期间旅行意向问卷调查”，最后从大量问卷调查表中随机抽取部分问卷，将所得数据整理并绘制成如下两幅不完整的统计图，下列说法错误的是（）

A、样本容量是500 B、扇形统计图中“大理”所占圆心角是 $90 °$ C、条形统计图中选择到“丽江”的旅游人数是155人 D、如果春节期间选择到云南景区旅游的总游客人数大约是100万，那么选择到西双版纳的游客人数约为16万

查看试题解析
10. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ，对角线 $B D$ 经过圆心，已知 $⊙ O$ 的半径为5，弦 $B C$ 为8，则 $s i n ∠ C A D$ 的值是（）

A、 $\frac{5}{8}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{3}{5}$

查看试题解析
11. 按一定规律排列的一列数依次为 $a^{2}$ ， $- \frac{a^{5}}{3}$ ， $\frac{a^{10}}{5}$ ， $- \frac{a^{17}}{7}$ ， …，按此规律排列下去，这组数中的第8个数是（）

A、 $- \frac{a^{50}}{15}$ B、 $\frac{a^{65}}{17}$ C、 $- \frac{a^{65}}{15}$ D、 $- \frac{a^{50}}{17}$

查看试题解析
12. 若关于x的不等式组 ${\begin{array}{l} 3 (x - 2) \geq 2 (2 x - 5) \\ \frac{2 x + 5}{2} \geq a + 1 \end{array}$ 有且只有7个整数解，则a的取值范围是（）

A、 $- \frac{5}{2} \leq a < - \frac{3}{2}$ B、 $- \frac{5}{2} < a \leq - \frac{3}{2}$ C、 $- \frac{3}{2} < a \leq - \frac{1}{2}$ D、 $- \frac{3}{2} \leq a < - \frac{1}{2}$

查看试题解析

二、填空题

13. 若 $\frac{1}{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
14. 若点 $A (2 ， - 1)$ 关于原点的对称点为点B，则点B的坐标是．

查看试题解析
15. 分解因式： $4 x^{2} - 16$ = ．

查看试题解析
16. 大瑞铁路东起大理站，西至瑞丽站，分为大保段和保瑞段，2022年7月大瑞铁路大保段开通运营，保山市结束了不通火车的历史．已知大理到瑞丽全程公路长约为540千米，高铁开通后，高铁路程比公路路程少了210千米，高铁的平均速度比公路的平均速度每小时快57千米，且所花时间少3小时．设高铁速度为x千米/时，则根据题意列方程为．

查看试题解析

三、解答题

17. 先化简，再求值： $(\frac{x + 2}{x^{2} - 1}) \div (1 + \frac{3}{x - 1})$ ，其中 $x = \sqrt{2}$ ．

查看试题解析
18. 如图， $A C$ 为菱形 $A B C D$ 的对角线，点E在 $A C$ 的延长线上，且 $∠ E = ∠ A B C$ ．求证： $△ A C D ∽ △ A B E$ ．

查看试题解析
19. 在二十大召开后，全国各地民众自发积极学习二十大精神，许多地方还组织各种形式的“二十大知识竞赛”．某校有4名（3名男教师与1名女教师）教师报名参加了“二十大网络知识竞赛”，每一名老师被选到的可能性都相同．

(1)、若从中选出一名教师代表学校参加“二十大网络知识竞赛”，选到男教师的概率为．

(2)、若需要派两名老师代表学校参加“二十大网络知识竞赛”，请用列表法或画树状图法（树状图也称树形图），求出两名教师都是男教师的概率P．

查看试题解析
20. 随着网络发展，电子产品大量普及，许多人都静不下心来读名著．为了倡导更多学生加入读名著活动，某校开展了一次“最近你读名著了吗？”的活动，调查学生近三年所读名著的数量．该校随机抽取100名学生“近三年读名著数量”的数据，根据调查数据绘制出下面的统计表．
近三年读名著数量
1本
2本
3本
4本
5本
6本
7本
8本
人数
1
5
11
20
24
22
12
5
请根据以上表格信息进行分析：

(1)、直接写出学生“近三年读名著数量”的众数和中位数．

(2)、求学生“近三年读名著数量”的平均数．

查看试题解析
21. 如图，四边形 $A B C D$ 的对角线 $A C ， B D$ 交于点O，且 $A B = A D ， C B = C D$ ， E是 $A O$ 上一点，连接 $B E ， D E$ ．

(1)、求证： $△ A B C ≅ △ A D C$ ．

(2)、若 $E O = C O$ ，试判断四边形 $B C D E$ 的形状，并说明理由．

查看试题解析
22. 为推进我省“绿美家园”建设步伐，某小区决定对小区广场进行改造，在广场周边种植景观树，通过市场调查，3棵甲景观树与1棵乙景观树种植费用为570元；1棵甲景观树与2棵乙景观树种植费用为390元．

(1)、甲、乙两种景观树每棵种植费用分别为多少元？

(2)、如果小区计划购进两种景观树共60棵，且甲景观树数量不低于乙景观树数量的一半，设购进甲景观树x棵，种植总费用为y元，写出y关于x的函数关系式，并求出最少种植费用．

查看试题解析
23. 如图， $A B$ 为 $⊙ O$ 的直径，E为 $A B$ 的延长线上一点，过点E作 $⊙ O$ 的切线，切点为点C，连接 $A C$ ， $B C$ ，过点A作 $A D ⊥ E C$ 交延长线于点D．

(1)、求证： $∠ B C E = ∠ D A C$ ．

(2)、若 $B E = 2$ ， $C E = 4$ ，求 $A D$ 的长．

查看试题解析
24. 如图，抛物线 $y = x^{2} + b x + c$ 与y轴交于点 $A (0 ， - \frac{1}{2})$ ，顶点坐标为 $B (- \frac{1}{2} ， - \frac{3}{4})$ ， C是x轴上一动点．

(1)、求b，c的值．

(2)、当 $△ A B C$ 周长最小时，求点C的坐标．

(3)、设m是抛物线 $y = x^{2} + b x + c$ 与x轴的交点的横坐标，求 $6 m^{5} + 10 m^{4} + 3 m^{3} + 2 m^{2} + m - 2023$ 的值．

查看试题解析

近三年读名著数量	1本	2本	3本	4本	5本	6本	7本	8本
人数	1	5	11	20	24	22	12	5