云南省丽江市2023年中考二模数学试卷
试卷更新日期:2023-06-19 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 截至2022年6月2日,世界第四大水电站——云南昭通溪洛渡水电站累计生产清洁电能突破5000亿千瓦时,相当于替代标准煤约1.52亿吨,减排二氧化碳约4.16亿.5000亿用科学记数法表示为( )
 A、 B、 C、 D、3. 如图是小明学习“探索直线平行的条件”时用到的学具,经测量 , 要使木条a与b平行,则的度数应为( )
A、 B、 C、 D、3. 如图是小明学习“探索直线平行的条件”时用到的学具,经测量 , 要使木条a与b平行,则的度数应为( ) A、45° B、75° C、105° D、135°4. 从班上13名排球队员中,挑选7名个头高的参加校排球比赛.若这13名队员的身高各不相同,其中队员小明想知道自己能否入选,只需知道这13名队员身高数据的( )A、平均数 B、中位数 C、最大值 D、方差5. 下列运算正确的是( )A、 B、 C、 D、6. 某几何体如图所示,该几何体的左视图是( )
A、45° B、75° C、105° D、135°4. 从班上13名排球队员中,挑选7名个头高的参加校排球比赛.若这13名队员的身高各不相同,其中队员小明想知道自己能否入选,只需知道这13名队员身高数据的( )A、平均数 B、中位数 C、最大值 D、方差5. 下列运算正确的是( )A、 B、 C、 D、6. 某几何体如图所示,该几何体的左视图是( )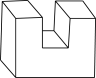 A、
A、 B、
B、 C、
C、 D、
D、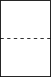 7. 把不等式x﹣1<2的解集在数轴上表示出来,正确的是( )A、
7. 把不等式x﹣1<2的解集在数轴上表示出来,正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 在中,弦垂直平分半径 , 点在上(不与点 , 重合),则的度数为( )A、 B、 C、或 D、或9. 如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC边相切,分别交AB,AC于D,E,则图中阴影部分的面积是( )
8. 在中,弦垂直平分半径 , 点在上(不与点 , 重合),则的度数为( )A、 B、 C、或 D、或9. 如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC边相切,分别交AB,AC于D,E,则图中阴影部分的面积是( )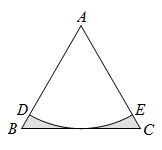 A、 B、 C、 D、10. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )A、 B、 C、 D、11. 按一定规律排列的等式:……,按此规律( )A、 B、 C、 D、12. 如图,在矩形ABCD中,AB<BC,连接AC,分别以点A,C为圆心,大于AC的长为半径画弧,两弧交于点M,N,直线MN分别交AD,BC于点E,F.下列结论:
A、 B、 C、 D、10. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )A、 B、 C、 D、11. 按一定规律排列的等式:……,按此规律( )A、 B、 C、 D、12. 如图,在矩形ABCD中,AB<BC,连接AC,分别以点A,C为圆心,大于AC的长为半径画弧,两弧交于点M,N,直线MN分别交AD,BC于点E,F.下列结论:①四边形AECF是菱形;②∠AFB=2∠ACB;③AC•EF=CF•CD;④若AF平分∠BAC,则CF=2BF.
其中正确结论的个数是( )
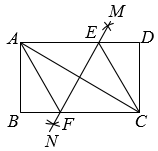 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
13. 一个正多边形的每个外角为60°,那么这个正多边形的内角和是。14. 因式分解: .15. 如图,是等边三角形,点在轴的正半轴上()的图象上,则的面积为 .
 16. 若函数 的图像与x轴有且只有一个交点,则a的值为 .
16. 若函数 的图像与x轴有且只有一个交点,则a的值为 .
三、解答题
-
17. 计算: .18. 为积极落实“双减”政策,让作业布置更加精准高效,某市教育部门对某中学九年级部分学生每天完成作业所用的时间进行调查,并用得到的数据绘制了如下不完整的统计图,根据图中信息解答下列问题:
调查部分学生每天完成作业所用时间的统计图
 (1)、本次共调查了 ▲ 名学生,并补全上面条形统计图.(2)、本次抽查学生每天完成作业所用时间的中位数为小时,众数为小时.(3)、该校九年级有1700名学生,请你估计九年级学生中,每天完成作业所用时间为2小时的学生约有多少人?19. 某地修建了一座以“讲好隆平故事,厚植种子情怀”为主题的半径为800米的圆形纪念园.如图,纪念园中心点A位于C村西南方向和B村南偏东60°方向上,C村在B村的正东方向且两村相距2.4千米.有关部门计划在B、C两村之间修一条笔直的公路来连接两村.问该公路是否穿过纪念园?试通过计算加以说明. (参考数据:≈1.73,≈1.41)
(1)、本次共调查了 ▲ 名学生,并补全上面条形统计图.(2)、本次抽查学生每天完成作业所用时间的中位数为小时,众数为小时.(3)、该校九年级有1700名学生,请你估计九年级学生中,每天完成作业所用时间为2小时的学生约有多少人?19. 某地修建了一座以“讲好隆平故事,厚植种子情怀”为主题的半径为800米的圆形纪念园.如图,纪念园中心点A位于C村西南方向和B村南偏东60°方向上,C村在B村的正东方向且两村相距2.4千米.有关部门计划在B、C两村之间修一条笔直的公路来连接两村.问该公路是否穿过纪念园?试通过计算加以说明. (参考数据:≈1.73,≈1.41)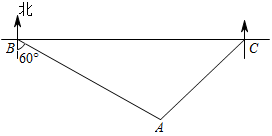 20. 小明与小刚做游戏,在甲、乙两个不透明的口袋中,分别装有完全一样的小球,其中甲口袋中的4个小球上分别标有数字1,2,3,4,乙口袋中的3个小球分别标有数字2,3,4,小明先从甲袋中随意摸出一个小球,记下数字为x,再从乙袋中随机摸出一个小球,记下数字为y.(1)、请用列表或画树状图的方法表示出所有可能出现的结果;(2)、若x,y都是方程的解时,则小明获胜;若x,y都不是方程的解时,则小刚获胜,它们谁获胜的概率大?请说明理由.21. 如图, 中, , 相交于点 , , 分别是 , 的中点.
20. 小明与小刚做游戏,在甲、乙两个不透明的口袋中,分别装有完全一样的小球,其中甲口袋中的4个小球上分别标有数字1,2,3,4,乙口袋中的3个小球分别标有数字2,3,4,小明先从甲袋中随意摸出一个小球,记下数字为x,再从乙袋中随机摸出一个小球,记下数字为y.(1)、请用列表或画树状图的方法表示出所有可能出现的结果;(2)、若x,y都是方程的解时,则小明获胜;若x,y都不是方程的解时,则小刚获胜,它们谁获胜的概率大?请说明理由.21. 如图, 中, , 相交于点 , , 分别是 , 的中点. (1)、求证: ;(2)、设 ,当 为何值时,四边形 是矩形?请说明理由.22. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现猪肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒.(1)、求猪肉粽和豆沙粽每盒的进价;(2)、设猪肉粽每盒售价x元 表示该商家每天销售猪肉粽的利润(单位:元),求y关于x的函数解析式并求最大利润.23. 为弘扬民族传统体育文化,某校将传统游戏“滚铁环”列入了校运动会的比赛项目.滚铁环器材由铁环和推杆组成.小明对滚铁环的启动阶段进行了研究,如图,滚铁环时,铁环⊙O与水平地面相切于点C,推杆AB与铅垂线AD的夹角为∠BAD,点O,A,B,C,D在同一平面内.当推杆AB与铁环⊙O相切于点B时,手上的力量通过切点B传递到铁环上,会有较好的启动效果.
(1)、求证: ;(2)、设 ,当 为何值时,四边形 是矩形?请说明理由.22. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现猪肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒.(1)、求猪肉粽和豆沙粽每盒的进价;(2)、设猪肉粽每盒售价x元 表示该商家每天销售猪肉粽的利润(单位:元),求y关于x的函数解析式并求最大利润.23. 为弘扬民族传统体育文化,某校将传统游戏“滚铁环”列入了校运动会的比赛项目.滚铁环器材由铁环和推杆组成.小明对滚铁环的启动阶段进行了研究,如图,滚铁环时,铁环⊙O与水平地面相切于点C,推杆AB与铅垂线AD的夹角为∠BAD,点O,A,B,C,D在同一平面内.当推杆AB与铁环⊙O相切于点B时,手上的力量通过切点B传递到铁环上,会有较好的启动效果.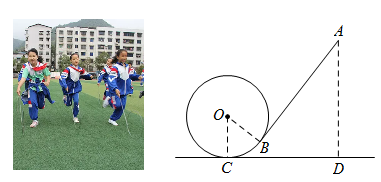 (1)、求证:∠BOC+∠BAD=90°.(2)、实践中发现,切点B只有在铁环上一定区域内时,才能保证铁环平稳启动.图中点B是该区域内最低位置,此时点A距地面的距离AD最小,测得 . 已知铁环⊙O的半径为25cm,推杆AB的长为75cm,求此时AD的长.24. 如图,抛物线(b,c是常数)的顶点为C,与x轴交于A,B两点, , , 点P为线段上的动点,过P作//交于点Q.
(1)、求证:∠BOC+∠BAD=90°.(2)、实践中发现,切点B只有在铁环上一定区域内时,才能保证铁环平稳启动.图中点B是该区域内最低位置,此时点A距地面的距离AD最小,测得 . 已知铁环⊙O的半径为25cm,推杆AB的长为75cm,求此时AD的长.24. 如图,抛物线(b,c是常数)的顶点为C,与x轴交于A,B两点, , , 点P为线段上的动点,过P作//交于点Q.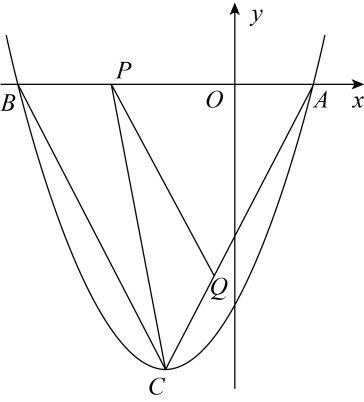 (1)、求该抛物线的解析式;(2)、求面积的最大值,并求此时P点坐标.
(1)、求该抛物线的解析式;(2)、求面积的最大值,并求此时P点坐标.