云南省昆明市盘龙区2023年中考二模数学试卷
试卷更新日期:2023-06-19 类型:中考模拟
一、单选题
-
1. 2022年,中国航天高密度发射任务有序实施,全年完成64次航天发射,发射航天器总质量约为197000kg,将数据197000用科学记数法表示为( )A、 B、 C、 D、2. 如图, , 点E在上,平分 , 若 , 则的度数为( )
 A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是由5个相同的正方体搭成的几何体,这个几何体的主视图是( )
A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是由5个相同的正方体搭成的几何体,这个几何体的主视图是( )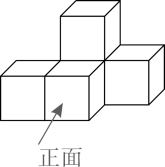 A、
A、 B、
B、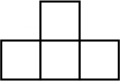 C、
C、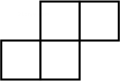 D、
D、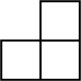 5. 若关于x的一元二次方程没有实数根,则k的值可以是( )A、 B、 C、 D、06. 如图,平分 , 于点 , 于点分别是、的中点,连接 . 若 , 则的长为( )
5. 若关于x的一元二次方程没有实数根,则k的值可以是( )A、 B、 C、 D、06. 如图,平分 , 于点 , 于点分别是、的中点,连接 . 若 , 则的长为( )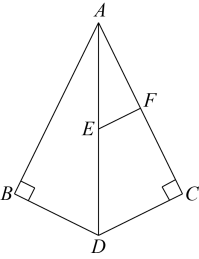 A、 B、 C、 D、7. 如图,是某水塘边的一块警示牌,牌面是正五边形,这个正五边形的每个内角为( )
A、 B、 C、 D、7. 如图,是某水塘边的一块警示牌,牌面是正五边形,这个正五边形的每个内角为( ) A、 B、 C、 D、8. 某校举办了校服设计大赛,并从七年级学生中随机抽取部分学生进行问卷调查,要求每名学生从4个获奖作品中选择一个自己最喜欢的作品,根据调查结果绘制成如图所示的两幅不完整的统计图.请你根据图中信息判断下列说法正确的是( )
A、 B、 C、 D、8. 某校举办了校服设计大赛,并从七年级学生中随机抽取部分学生进行问卷调查,要求每名学生从4个获奖作品中选择一个自己最喜欢的作品,根据调查结果绘制成如图所示的两幅不完整的统计图.请你根据图中信息判断下列说法正确的是( ) A、参加此次问卷调查的学生人数是45人 B、在条形统计图中,选择“作品2”的人数为15人 C、在扇形统计图中,选择“作品1”的学生所对应扇形的圆心角的度数是 D、在扇形统计图中,选择“作品3”的学生所占百分比为9. 如图,在天定山滑雪场滑雪,需从山脚下处乘缆车上山顶处,缆车索道与水平线所成的 , 若山的高度米,则缆车索道的长为( )
A、参加此次问卷调查的学生人数是45人 B、在条形统计图中,选择“作品2”的人数为15人 C、在扇形统计图中,选择“作品1”的学生所对应扇形的圆心角的度数是 D、在扇形统计图中,选择“作品3”的学生所占百分比为9. 如图,在天定山滑雪场滑雪,需从山脚下处乘缆车上山顶处,缆车索道与水平线所成的 , 若山的高度米,则缆车索道的长为( )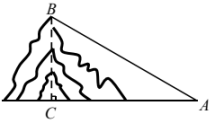 A、米 B、米 C、米 D、米10. 云南省坚持用习近平新时代中国特色社会主义思想铸魂育人,构建德智体美劳“五育并举”育人体系.某学校为加强劳动实践教育投入元购进了一批劳动工具,开展劳动实践教育后学生劳动积极性明显增强,需再次采购一批相同的劳动工具,已知第二批采购数量与第一批相同,但采购单价比第一批降低元,总费用为元.设第一批采购单价为元,则下列方程正确的是( )A、 B、 C、 D、11. 美术课上,小梅同学利用如图所示直径为1dm的圆形材料裁剪出一个扇形图案,已知扇形的圆心角 , 则扇形图案的面积为( )
A、米 B、米 C、米 D、米10. 云南省坚持用习近平新时代中国特色社会主义思想铸魂育人,构建德智体美劳“五育并举”育人体系.某学校为加强劳动实践教育投入元购进了一批劳动工具,开展劳动实践教育后学生劳动积极性明显增强,需再次采购一批相同的劳动工具,已知第二批采购数量与第一批相同,但采购单价比第一批降低元,总费用为元.设第一批采购单价为元,则下列方程正确的是( )A、 B、 C、 D、11. 美术课上,小梅同学利用如图所示直径为1dm的圆形材料裁剪出一个扇形图案,已知扇形的圆心角 , 则扇形图案的面积为( ) A、 B、 C、 D、12. 用黑白两种颜色的正六边形地板砖按如图所示的规律,拼成如下若干地板图案,为探索出第个图案中白色地板砖的块数,同学们列出以下三种不同的代数式:①;②;③ . 其中正确的代数式有( )
A、 B、 C、 D、12. 用黑白两种颜色的正六边形地板砖按如图所示的规律,拼成如下若干地板图案,为探索出第个图案中白色地板砖的块数,同学们列出以下三种不同的代数式:①;②;③ . 其中正确的代数式有( ) A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题
-
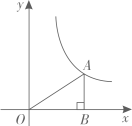
13. 若在实数范围内有意义,则实数x的取值范围是 .14. 如图,点A在反比例函数的图象上,过点A作轴于点B,若的面积为2,则该反比例函数的解析式是 .
 15. 分解因式:x2+2x+1= .
15. 分解因式:x2+2x+1= .
三、解答题
-
16. 如图,在矩形中, , , 点E是边上的一点,连接 , 将沿翻折,使点D恰好落在边上的点F处,求的值.
 17. 计算:18. 如图,在中, , , 于点E,且 . 求证: .
17. 计算:18. 如图,在中, , , 于点E,且 . 求证: . 19. 在祖国植物的百花园中,云南素有“植物王国”之称,云南枸杞的主要产区为禄劝县与景东县,某枸杞种植改良实验基地对新培育的甲、乙两个枸杞品种各试种一亩,从两块试验地中各随机抽取10棵,对其产量(千克/棵)进行整理分析.下面给出了部分信息:
19. 在祖国植物的百花园中,云南素有“植物王国”之称,云南枸杞的主要产区为禄劝县与景东县,某枸杞种植改良实验基地对新培育的甲、乙两个枸杞品种各试种一亩,从两块试验地中各随机抽取10棵,对其产量(千克/棵)进行整理分析.下面给出了部分信息:甲品种:2.0,3.2,3.1,3.2,3.1,2.5,3.2,3.6,3.8,3.9
乙品种:如图所示

甲、乙品种产量统计表:
品种
平均数
中位数
众数
方差
甲品种
3.16
a
3.2
0.29
乙品种
3.16
3.3
b
0.15
根据以上信息,完成下列问题:
(1)、填空: , ;(2)、若乙品种种植3000棵,估计其产量不低于3.16千克的棵树;(3)、请结合以上统计量中的某一方面简要说明那个品种更好.20. 云南是中国少数民族最多的省份,除了汉族外,还聚居着26个民族,全省少数民族人口占总人口的近三分之一,早在氏族社会时期,云南就生活着“羌、濮、越”三大族群,他们是云南最早的先民,后经历代的不断演变,到了明清时代,各族的分布才趋于稳定.学校某社团想在三大族群中挑选两个族群进行研究,在一只不透明的袋子中装有3个大小、质地完全相同的乒乓球,球面上分别标有“羌”、“濮”、“越”,搅匀后先从袋子中任意摸出1个球,记录文字后放回,搅匀后再从袋子中任意摸出1个球,记录文字.(1)、从袋中任意摸出一个乒乓球是标有“羌”字乒乓球的概率是;(2)、用列表法或画树状图法中的一种方法,求两次摸到不同族群的乒乓球的概率.21. 如图,在正方形中,对角线相交于点O,点E,F是对角线上的两点,且 , 连接 . (1)、求证:四边形是菱形;(2)、若 , , 求菱形的边长.22. 云南某旅游景区购进一批文创产品,40天销售完毕.根据记录的数据发现,日销售量y(件)与销售时间x(天)之间的关系式是 , 销售单价p(元/件)与销售时间x(天)之间的函数关系如图所示.
(1)、求证:四边形是菱形;(2)、若 , , 求菱形的边长.22. 云南某旅游景区购进一批文创产品,40天销售完毕.根据记录的数据发现,日销售量y(件)与销售时间x(天)之间的关系式是 , 销售单价p(元/件)与销售时间x(天)之间的函数关系如图所示. (1)、第15天的日销售量为件;(2)、当时,求日销售额的最大值.23. 【问题引入】
(1)、第15天的日销售量为件;(2)、当时,求日销售额的最大值.23. 【问题引入】古希腊几何学家海伦和我国南宋数学家秦九韶都曾提出利用三角形的三边求面积的公式,称为海伦-秦九韶公式,如果一个三角形的三边长分别是 , 记 , 那么三角形的面积为: , 在中, , , 所对的边长分别为 , 若 , , , 则的面积为6;
【问题探索】
如图一,在中,设 , , , , 是的内切圆,分别与的延长线、的延长线以及线段均只有一个公共点,的半径为 , 的半径为 .
 (1)、分析与证明:
(1)、分析与证明:如图二,连接 , 则被划分为三个小三角形,用表示的面积,即 . 那么是否成立?请证明你的结论.
(2)、理解与应用:当 , , 时,求的面积.
24. 在平面直角坐标系中,已知抛物线(t为常数).(1)、当抛物线过点时,求该抛物线的函数解析式;(2)、当时,抛物线(t为常数)的最低点与直线的距离为 , 求t的值.