云南省昆明市官渡区2023年中考二模数学试卷
试卷更新日期:2023-06-19 类型:中考模拟
一、单选题
-
1. 的值等于( )A、2 B、-2 C、±2 D、22. 在科幻小说《三体》中,制造太空电梯的材料是科学家汪淼发明的一种具有超高强度纳米丝的“飞刃”,已知“飞刃”的直径为 , 用科学记数法表示为 , 其中为( )A、 B、6 C、 D、73. 如图,直线 ,若 , 则的度数为( )
 A、 B、 C、 D、4. 如图是某个几何体的三视图,该几何体是( ).
A、 B、 C、 D、4. 如图是某个几何体的三视图,该几何体是( ).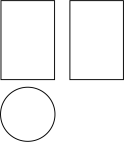 A、圆柱 B、圆锥 C、四棱柱 D、四棱锥5. 蝴蝶标本可以近似地看作轴对称图形,如图,将一只蝴蝶标本放在平面直角坐标系中,若图中点的坐标为 , 则其关于轴对称的点的坐标为( )
A、圆柱 B、圆锥 C、四棱柱 D、四棱锥5. 蝴蝶标本可以近似地看作轴对称图形,如图,将一只蝴蝶标本放在平面直角坐标系中,若图中点的坐标为 , 则其关于轴对称的点的坐标为( ) A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 分形的概念是由数学家本华曼德博提出的,如图是分形的一种,第1个图案有2个三角形,第2个图案有4个三角形,第3个图案有8个三角形,第4个图案有16个三角形,…,按此规律分形得到第个图案中三角形的个数是( )
A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 分形的概念是由数学家本华曼德博提出的,如图是分形的一种,第1个图案有2个三角形,第2个图案有4个三角形,第3个图案有8个三角形,第4个图案有16个三角形,…,按此规律分形得到第个图案中三角形的个数是( ) A、 B、 C、 D、8. 小孔成像是光在均匀介质中沿直线传播形成的一种物理现象,两千四百多年前,我国学者墨子就在《墨经》中记载了小孔成像实验的做法与成因,图1是某次小孔成像实验图,抽象为数学问题如图2:与交于点 , , 若点到的距离为 , 点到的距离为 , 蜡烛火焰的高度是 , 则蜡烛火焰倒立的像的高度是( )
A、 B、 C、 D、8. 小孔成像是光在均匀介质中沿直线传播形成的一种物理现象,两千四百多年前,我国学者墨子就在《墨经》中记载了小孔成像实验的做法与成因,图1是某次小孔成像实验图,抽象为数学问题如图2:与交于点 , , 若点到的距离为 , 点到的距离为 , 蜡烛火焰的高度是 , 则蜡烛火焰倒立的像的高度是( ) A、 B、 C、 D、9. 如图,点是反比例函数的图象上一点,过点作轴的垂线交轴于点 , 若点是轴上一点, , 则的值为( )
A、 B、 C、 D、9. 如图,点是反比例函数的图象上一点,过点作轴的垂线交轴于点 , 若点是轴上一点, , 则的值为( )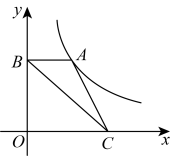 A、1 B、 C、2 D、10. 如图是小云和小南根据各自家庭某月的生活支出情况绘制的统计图.关于这个月支出情况判断正确的是( )
A、1 B、 C、2 D、10. 如图是小云和小南根据各自家庭某月的生活支出情况绘制的统计图.关于这个月支出情况判断正确的是( )小云家生活支出情况统计图 小南家生活支出情况统计图
 A、小云家的总支出比小南家的总支出多 B、小云家的“教育支出”比小南家“教育支出”多 C、小云家和小南家的“其他支出”占总支出的百分比相同 D、小云家和小南家的“食品支出”占总支出的百分比相同11. “行人守法,安全过街”不仅体现了对生命的尊重,也体现了公民的文明素质,更反映了城市的文明程度.如图,官渡区森林公园路口的斑马线为横穿双向行驶车道,其中米,在绿灯亮时,小官共用秒通过路段,其中通过路段的速度是通过路段速度的倍,则小官通过路段的速度是( )
A、小云家的总支出比小南家的总支出多 B、小云家的“教育支出”比小南家“教育支出”多 C、小云家和小南家的“其他支出”占总支出的百分比相同 D、小云家和小南家的“食品支出”占总支出的百分比相同11. “行人守法,安全过街”不仅体现了对生命的尊重,也体现了公民的文明素质,更反映了城市的文明程度.如图,官渡区森林公园路口的斑马线为横穿双向行驶车道,其中米,在绿灯亮时,小官共用秒通过路段,其中通过路段的速度是通过路段速度的倍,则小官通过路段的速度是( )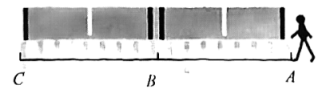 A、米/秒 B、米/秒 C、米/秒 D、米/秒12. 松华坝水库地处昆明北郊,是昆明市的重要水源,被称为“昆明头上的一碗水”,水库周边遍布森林与湿地,呈现出一幅纯净自然的和谐生态画卷.如图,大坝某段横截面迎水坡的坡度(),若坝高 , 则坡面的水平宽度长度约为( )(参考数据: , , )
A、米/秒 B、米/秒 C、米/秒 D、米/秒12. 松华坝水库地处昆明北郊,是昆明市的重要水源,被称为“昆明头上的一碗水”,水库周边遍布森林与湿地,呈现出一幅纯净自然的和谐生态画卷.如图,大坝某段横截面迎水坡的坡度(),若坝高 , 则坡面的水平宽度长度约为( )(参考数据: , , )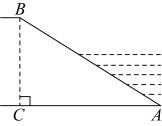 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
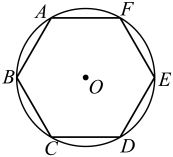
13. 若有意义,则的取值范围是 .14. 六边形象征六合、六顺之意,比如首饰盒、古建筑的窗户、古井口、佛塔等等,化学上一些分子结构、物理学上的螺母,也采用六边形.从工程角度来看,正六边形是最稳定和对称的.如图,正六边形内接于 , 若正六边形的边长为6,则劣弧的长为(结果保留).
 15. 如图,在平面直角坐标中,抛物线和直线交于点和点 , 则不等式的解集为 .
15. 如图,在平面直角坐标中,抛物线和直线交于点和点 , 则不等式的解集为 . 16. 如图,扇形中, , , 分别以点 , 点为圆心,大于的长为半径画弧,两弧交于 , 两点,沿直线折叠使得点与点重合,则阴影部分的面积为 .
16. 如图,扇形中, , , 分别以点 , 点为圆心,大于的长为半径画弧,两弧交于 , 两点,沿直线折叠使得点与点重合,则阴影部分的面积为 .
三、解答题
-
17. 先化简,再求值: , 其中 .18. “倍长中线法”是解决几何问题的重要方法.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,具体做法是:如图,是的中线,延长到 , 使 , 连接 , 构造出和 . 求证: .
 19. 随着科幻电影的崛起,层出不穷的“硬核科技”元素引起人们的热烈讨论,例如太空电梯,数字生命,重核聚变行星发动机,超级量子计算机,人工智能,机械外骨骼等,强大的科技会促使科幻走进现实.为激发中学生对科技创新的热情,某校在七、八年级学生中举行了青少年科技创新大赛,赛后从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
19. 随着科幻电影的崛起,层出不穷的“硬核科技”元素引起人们的热烈讨论,例如太空电梯,数字生命,重核聚变行星发动机,超级量子计算机,人工智能,机械外骨骼等,强大的科技会促使科幻走进现实.为激发中学生对科技创新的热情,某校在七、八年级学生中举行了青少年科技创新大赛,赛后从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:[收集数据]:
七年级:94,87,86,85,83,81,80,80,79,79,77,76,75,75,75,75,73,71,70,59.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
[整理数据]:
七年级
0
1
0
11
7
1
八年级
1
0
0
7
2
[分析数据]:
平均数
众数
中位数
七年级
78
75
八年级
78
81
80.5
[应用数据]:
(1)、填表: , ;(2)、该校七、八年级各有300名学生,估计这两个年级在本次科技创新大赛中成绩在90分以上的学生共有多少人?(3)、根据以上分析,你认为哪个年级科技创新大赛的成绩更好?请说明理由.20. 西双版纳作为国内唯一的热带雨林城市,凭借其四季如春的气候、蓝天白云的纯净环境、多彩的民族文化和独特的东南亚风情,吸引着来自世界各地的游客,五一假期,小昆和小明乘坐动车到西双版纳旅游,当天符合他们出行安排的车次有四趟,具体车次及编号如下图(假设他们分别购买各自车票,且选择每个车次的可能性相同):编号
车次



 (1)、小昆选择车次的概率是;(2)、用列表或画树状图的方法,求小昆和小明选到同一车次的概率.21. 如图,是的直径, , 都是上的点,且平分 , 过点作的垂线交的延长线于点 , 交的延长线于点 .
(1)、小昆选择车次的概率是;(2)、用列表或画树状图的方法,求小昆和小明选到同一车次的概率.21. 如图,是的直径, , 都是上的点,且平分 , 过点作的垂线交的延长线于点 , 交的延长线于点 . (1)、求证:是的切线;(2)、若 , , 求的长.22. 某校九年级决定购买学习用具对本学期数学表现优秀的同学进行奖励,计划购买甲、乙两款圆规套装,已知甲款圆规套装所需费用(元)与购买数量(套)之间的函数关系如图所示,乙款圆规套装单价为每套8元.
(1)、求证:是的切线;(2)、若 , , 求的长.22. 某校九年级决定购买学习用具对本学期数学表现优秀的同学进行奖励,计划购买甲、乙两款圆规套装,已知甲款圆规套装所需费用(元)与购买数量(套)之间的函数关系如图所示,乙款圆规套装单价为每套8元.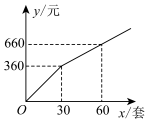 (1)、求出与的函数关系式:(2)、若甲、乙两款圆规套装共需65套,且甲款圆规套装的数量不少于乙款圆规套装的数量.设购买总费用为元,如何设计购买方案,使总费用最低?最低总费用多少元?
(1)、求出与的函数关系式:(2)、若甲、乙两款圆规套装共需65套,且甲款圆规套装的数量不少于乙款圆规套装的数量.设购买总费用为元,如何设计购买方案,使总费用最低?最低总费用多少元?
