云南省楚雄州双柏县2023年中考一模数学试卷

试卷更新日期：2023-06-19 类型：中考模拟

进入出卷网下载

一、单选题

1. 温度计零上 $5 ℃$ 记为 $+ 5 ℃$ ，那么零下 $8 ℃$ 记为（）

A、 $+ 8 ℃$ B、 $- 8 ℃$ C、 $+ 13 ℃$ D、 $- 3 ℃$

查看试题解析
2. 4的平方根是（）

A、±2 B、﹣2 C、2 D、 $\sqrt{4}$

查看试题解析
3. 如图， $A B ∥ C D$ ， $C E$ 平分 $∠ A C D$ ，若 $∠ A = 120 °$ ，则 $∠ A E C$ 的度数为（）

A、 $30 °$ B、 $40 °$ C、 $45 °$ D、 $50 °$

查看试题解析
4. 已知一元二次方程 $m x^{2} + m x - 1 = 0$ 有两个相等的实数根，则 $m$ 的值为（）

A、 $m = 0$ B、 $m = - 4$ C、 $m = 0$ ，或 $m = 4$ D、 $m = 0$ ，或 $m = - 4$

查看试题解析
5. 如图，在 $△ A B C$ 中， $A B = A C ， ∠ A B C = 45 °$ ， $A D ⊥ B C$ 于点D，若 $B C = 8$ ，则 $A D =$ （　　）

A、8 B、4 C、4 $\sqrt{3}$ D、4 $\sqrt{2}$

查看试题解析
6. 若圆锥的底面半径是 $2 c m$ ，侧面展开扇形的面积为 $4 π c m^{2}$ ，则圆锥的母线长为（）

A、 $2 c m$ B、 $4 c m$ C、 $2 π c m$ D、 $4 π c m$

查看试题解析
7. 若点 $A (a ， b)$ 在第二象限，则点 $B (a ， - b)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“年”字一面的相对面上的字是（）

A、百 B、党 C、迎 D、喜

查看试题解析
9. 按一定规律排列的单项式： $x^{2} ， - 3 x^{3} ， 5 x^{4} ， - 7 x^{5} ， 9 x^{6}$ ， …，第n个单项式是（）

A、 ${(- 1)}^{n}^{+ 1} \cdot (2 n - 1) n {x^{n}}^{+ 1}$ B、 ${(- 1)}^{n}^{+ 1} \cdot (2 n - 1) {x^{n}}^{+ 1}$ C、 ${(- 1)}^{n}^{- 1} \cdot (2 n - 1) {x^{n}}^{- 1}$ D、 ${(- 1)}^{n}^{+ 1} \cdot (2 n + 1) {x^{n}}^{+ 1}$

查看试题解析
10. 为了弘扬我国古代数学发展的伟大成就，让学生深刻体会数学的魅力，某校举办了一次数学文化知识竞赛，并随机抽取了部分参赛学生的成绩，整理如表：
成绩 $/$ 分
$80$
$85$
$90$
$95$
人数 $/$ 人
$4$
$6$
$8$
$2$
根据表中的信息可知，这些参赛学生成绩的中位数和众数分别是（）

A、 $87.5$ ， $90$ B、 $90$ ， $90$ C、 $87.5$ ， $85$ D、 $90$ ， $85$

查看试题解析
11. 如图，点A，B，C在边长为1的正方形网格格点上，则 $A B$ 边上的高为（）

A、 $\frac{6 \sqrt{5}}{5}$ B、 $\frac{6}{\sqrt{5}}$ C、 $\frac{\sqrt{5}}{6}$ D、 $\sqrt{5}$

查看试题解析
12. 昆明市区与石林风景区相距约为84千米，甲驾驶小轿车，乙乘坐旅游大巴，从昆明市区走同一路线去石林风景区，甲比乙晚出发20分钟，最后两人同时到达石林风景区，已知小轿车的速度是旅游大巴速度的1.2倍，设旅游大巴的速度为 $x$ 千米/小时，则所列方程正确的是（）

A、 $\frac{84}{x} = \frac{84}{1.2 x} + 20$ B、 $\frac{84}{x} = \frac{84}{1.2 x} - 20$ C、 $\frac{84}{x} = \frac{84}{1.2 x} - \frac{1}{3}$ D、 $\frac{84}{x} = \frac{84}{1.2 x} + \frac{1}{3}$

查看试题解析

二、填空题

13. 因式分解： $x^{2} + 2 x + 1 =$ .

查看试题解析
14. 一个多边形的内角和是其外角和的4倍，则这个多边形的边数是.

查看试题解析
15. 已知正比例函数 $y = k x$ 与反比例函数 $y = \frac{1}{x}$ 的图象过点 $P (a ， - 1)$ ，则这个正比例函数解析式是．

查看试题解析
16. 在⊙O中，若弦 $B C$ 垂直平分半径 $O A$ ，则弦 $B C$ 所对的圆周角等于°.

查看试题解析

三、解答题

17. 计算： $2 c o s 60 ° - (π - 3.14)^{0} + (- \frac{1}{3})^{- 2} + \frac{3}{4} \times (- 8)$ ．

查看试题解析
18. 如图，点C是 $A E$ 上一点， $C D$ 交 $E B$ 于点F， $C F = D F$ ， $E A ∥ D B$ ，求证： $E F = B F$ ．

查看试题解析
19. 为了传承中华优秀传统文化，某校组织了一次八年级 $350$ 名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于 $50$ 分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中若干名学生的成绩作为样本进行整理，得到下列不完整的统计图表：
比赛成绩统计表
成绩 $x /$ 分
频数
频率
$50 \leq x < 60$
$2$
$0.04$
$60 \leq x < 70$
$6$
$0.12$
$70 \leq x < 80$
$9$
$b$
$80 \leq x < 90$
$a$
$0.36$
$90 \leq x \leq 100$
$15$
$0.30$
比赛成绩统计图
请根据所给信息，解答下列问题：

(1)、 $b =$ ；

(2)、请补全频数分布直方图；

(3)、若成绩在 $80$ 分以上（包括 $80$ 分）的为“优”等，则该年级参加这次比赛的 $350$ 名学生中成绩“优”等的约有多少人？

查看试题解析
20. 为“学习二十大，永远跟党走，奋进新征程”庆祝活动，某学校组织志愿者周末到社区进行学习宣讲，决定从 $A ， B ， C ， D$ 四名志愿者中通过抽签的方式确定两名志愿者参加．抽签规则：将四名志愿者的名字分别写在四张完全相同不透明卡片的正面，把四张卡片背面朝上，洗匀后放在桌面上，先从中随机抽取一张卡片，记下名字，再从剩余的三张卡片中随机抽取第二张，记下名字．

(1)、“ $B$ 志愿者被选中”是事件（填“随机”或“不可能”或“必然”）；

(2)、请你用列表法或画树状图法表示出这次抽签所有可能的结果，并求出 $C ， D$ 两名志愿者被选中的概率．

查看试题解析
21. 如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于H，连接OH．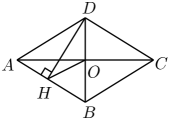

(1)、求证：∠OHD＝∠ODH；

(2)、若OC＝4，BD＝6，求菱形ABCD的周长和面积．

查看试题解析
22. 小李在某网店选中A、B两款玩偶，决定从该网店进货并销售．两款玩偶的进货价和销售价如下表：
类别
A款玩偶
B款玩偶
进货价（元/个）
40
30
销售价（元/个）
56
45

(1)、第一次小李用1100元购进了A、B两款玩偶共30个，求这两款玩偶各购进的数量．

(2)、第二次小李进货时，网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半．小李计划购进这两款玩偶共30个，应如何设计进货方案才能获得最大利润，最大利润是多少？请通过计算说明．

查看试题解析
23. 如图，AB是⊙O的直径，点E在AB的延长线上，AC平分∠DAE交⊙O于点C，AD⊥DE于点D．
（l）求证：直线DE是⊙O的切线．

(1)、如果BE=2，CE=4，求线段AD的长．

查看试题解析
24. 在直角坐标系中，设函数y＝ax²+bx+1（a，b是常数，a≠0）．

(1)、若该函数的图象经过（1，0）和（2，1）两点，求函数的表达式，并写出函数图象的顶点坐标；

(2)、已知a＝b＝1，当x＝p，q（p，q是实数，p≠q）时，该函数对应的函数值分别为P，Q．若p+q＝2，求证：P+Q＞6．

查看试题解析

成绩 $x /$ 分	频数	频率
$50 \leq x < 60$	$2$	$0.04$
$60 \leq x < 70$	$6$	$0.12$
$70 \leq x < 80$	$9$	$b$
$80 \leq x < 90$	$a$	$0.36$
$90 \leq x \leq 100$	$15$	$0.30$

类别	A款玩偶	B款玩偶
进货价（元/个）	40	30
销售价（元/个）	56	45

成绩 $/$ 分	$80$	$85$	$90$	$95$
人数 $/$ 人	$4$	$6$	$8$	$2$