云南省楚雄州双柏县2023年中考三模数学试卷
试卷更新日期:2023-06-19 类型:中考模拟
一、单选题
-
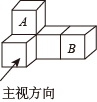
1. 在2,0, , 四个数中,最小的是( )A、 B、0 C、 D、22. 如图是由5个相同小正方体搭成的几何体,若将小正方体B放到小正方体A的正上方,则关于该几何体变化前后的三视图,下列说法正确的是( )
 A、主视图不变 B、左视图不变 C、俯视图不变 D、以上三种视图都改变3. 近来,中国芯片技术获得重大突破,7nm芯片已经量产,一举打破以美国为首的西方世界的技术封锁.已知 , 则用科学记数法可以表示为( )A、 B、 C、 D、4. 如图,直线 , 直线分别与相交于点A,B.小宇用尺规作图法按以下步骤作图:①以点A为圆心,以任意长为半径作弧交于点C,交于点D;②分别以C,D为圆心,以大于长为半径作弧,两弧在内交于点E;③作射线交于点F.若 , 则的度数为( )
A、主视图不变 B、左视图不变 C、俯视图不变 D、以上三种视图都改变3. 近来,中国芯片技术获得重大突破,7nm芯片已经量产,一举打破以美国为首的西方世界的技术封锁.已知 , 则用科学记数法可以表示为( )A、 B、 C、 D、4. 如图,直线 , 直线分别与相交于点A,B.小宇用尺规作图法按以下步骤作图:①以点A为圆心,以任意长为半径作弧交于点C,交于点D;②分别以C,D为圆心,以大于长为半径作弧,两弧在内交于点E;③作射线交于点F.若 , 则的度数为( )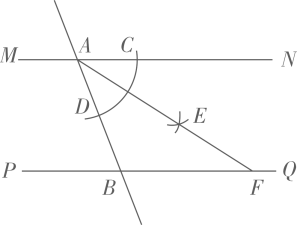 A、 B、 C、 D、5. 反比例函数的图象位于( )A、第一、三象限 B、第二、四象限 C、第一、四象限 D、第二、三象限6. 如图,一把梯子靠在垂直水平地面的墙上,梯子的长是6米.若梯子与地面的夹角为 , 则梯子底端到墙面的距离的长为( )米
A、 B、 C、 D、5. 反比例函数的图象位于( )A、第一、三象限 B、第二、四象限 C、第一、四象限 D、第二、三象限6. 如图,一把梯子靠在垂直水平地面的墙上,梯子的长是6米.若梯子与地面的夹角为 , 则梯子底端到墙面的距离的长为( )米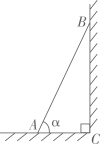 A、 B、 C、 D、7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,菊花1角硬币为外圆内正九边形的边缘异形币,则该正九边形一个内角的大小为( )
A、 B、 C、 D、7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,菊花1角硬币为外圆内正九边形的边缘异形币,则该正九边形一个内角的大小为( ) A、135° B、140° C、145° D、150°9. 关于x的一元二次方程有实数根,则k的取值范围是( )A、 B、且 C、且 D、10. 按一定规律排列的单项式: , , , , , …,第n个单项式为( )A、 B、 C、 D、11. 在创建文明城市的进程中,某市为美化城市环境,计划种植树木50万棵,由于志愿者的加入,实际每天植树比原计划多30%,结果提前2天完成任务,设原计划每天植树万棵,由题意得到的方程是( )A、 B、 C、 D、12. 如图,的斜边在y轴上, , 含角的顶点与原点重合,直角顶点C在第二象限.若将绕着原点顺时针旋转后得到 , 则点B的对应点的坐标是( )
A、135° B、140° C、145° D、150°9. 关于x的一元二次方程有实数根,则k的取值范围是( )A、 B、且 C、且 D、10. 按一定规律排列的单项式: , , , , , …,第n个单项式为( )A、 B、 C、 D、11. 在创建文明城市的进程中,某市为美化城市环境,计划种植树木50万棵,由于志愿者的加入,实际每天植树比原计划多30%,结果提前2天完成任务,设原计划每天植树万棵,由题意得到的方程是( )A、 B、 C、 D、12. 如图,的斜边在y轴上, , 含角的顶点与原点重合,直角顶点C在第二象限.若将绕着原点顺时针旋转后得到 , 则点B的对应点的坐标是( )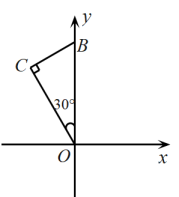 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
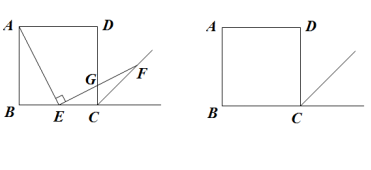
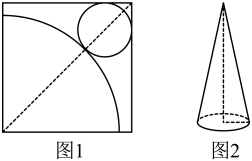
13. 分解因式:a2b﹣9b= .14. 若式子 有意义,则实数 的取值范围是.15. 如图(1),在正方形铁皮上剪下一个圆形和扇形,使之恰好围成如图(2)所示的一个圆锥模型,则圆的半径r与扇形的半径R之间的关系为 .
 16. 若 , 则 .
16. 若 , 则 .三、解答题
-
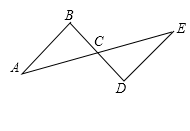
17. 计算: .18. 如图,和相交于点C, , . 求证: .
 19. 2020年5月28日,十三届全国人大三次会议表决通过了《中华人民共和国民法典》.它规范了我们从衣食住行到生老病死的大情小事,被称为“社会生活的百科全书”,是新中国第一部以法典命名的法律,在法律体系中居于基础性地位,也是市场经济的基本法.为了解人们对《民法典》的熟悉情况,王老师制作了问卷,随机对路人进行问卷调查,把调查结果分为四类:A(很了解),B(基本了解),C(听说过),D(没听过).调查结束后,王老师将调查结果绘制成如下两幅不完整的统计图,请你根据已有信息解答下列问题:
19. 2020年5月28日,十三届全国人大三次会议表决通过了《中华人民共和国民法典》.它规范了我们从衣食住行到生老病死的大情小事,被称为“社会生活的百科全书”,是新中国第一部以法典命名的法律,在法律体系中居于基础性地位,也是市场经济的基本法.为了解人们对《民法典》的熟悉情况,王老师制作了问卷,随机对路人进行问卷调查,把调查结果分为四类:A(很了解),B(基本了解),C(听说过),D(没听过).调查结束后,王老师将调查结果绘制成如下两幅不完整的统计图,请你根据已有信息解答下列问题: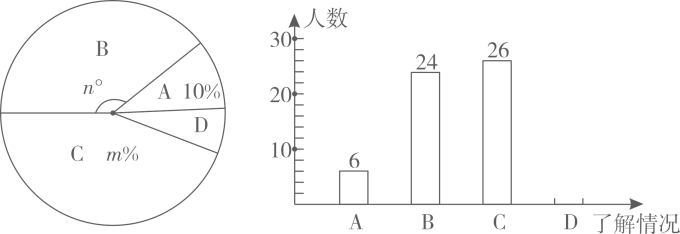 (1)、该调查的样本容量是: , , ;(2)、补全条形统计图;(3)、如果调查区域内有3600人,估计“基本了解”的人数有多少人?20. 在一个不透明的口袋里装有黑、白两种颜色的球共4个.某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回口袋中,不断重复.下表是活动进行中的一组统计数据:
(1)、该调查的样本容量是: , , ;(2)、补全条形统计图;(3)、如果调查区域内有3600人,估计“基本了解”的人数有多少人?20. 在一个不透明的口袋里装有黑、白两种颜色的球共4个.某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回口袋中,不断重复.下表是活动进行中的一组统计数据:摸球的次数n
2048
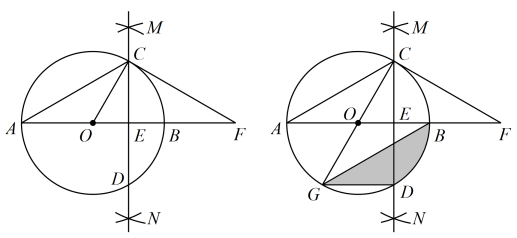
4040
10000
12000
摸到白球的次数m
1061
2048
4979
6019
摸到白球的频率
0.518
0.5069
0.4979
0.5016
(1)、请估计:当很大时,摸到白球的频率将会接近(精确到);(2)、试估算口袋中白球有多少个?(3)、若从中摸出一个球后不放回,再从余下的球中摸出一个,请用列表法或画树状图的方法(只需要选其中一种),求两次摸到的球的颜色相同的概率.21. 如图,抛物线的顶点为D,其图象交x轴于A,B两点,交y轴于点 , 点B的坐标为 .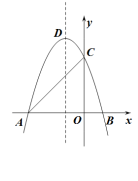 (1)、求抛物线的解析式;(2)、在抛物线的对称轴上是否存在点M,使得以A,C,M为顶点的三角形为等腰三角形?若存在,求出以为腰时点M的坐标;若不存在,请说明理由.22. 某中学开学初到商场购买A,B两种品牌的足球,购买A种品牌的足球50个,B种品牌的足球25个,共花费5000元.已知购买一个B种品牌的足球比购买一个A种品牌的足球需要多花20元.(1)、求购买一个A种品牌、一个B种品牌的足球各需多少元?(2)、为了响应习总书记“足球进校园”的号召,学校决定再次购进A,B两种品牌的足球50个,正好赶上商场对商品价格进行调整,A品牌足球的售价比第一次购买时提高5元,B品牌足球按第一次购买时售价的九折出售.如果学校此次购买A,B两种品牌足球的总费用不超过第一次花费的 , 且保证这次购买的B种品牌足球不少于33个,则这次学校有哪几种购买方案?
(1)、求抛物线的解析式;(2)、在抛物线的对称轴上是否存在点M,使得以A,C,M为顶点的三角形为等腰三角形?若存在,求出以为腰时点M的坐标;若不存在,请说明理由.22. 某中学开学初到商场购买A,B两种品牌的足球,购买A种品牌的足球50个,B种品牌的足球25个,共花费5000元.已知购买一个B种品牌的足球比购买一个A种品牌的足球需要多花20元.(1)、求购买一个A种品牌、一个B种品牌的足球各需多少元?(2)、为了响应习总书记“足球进校园”的号召,学校决定再次购进A,B两种品牌的足球50个,正好赶上商场对商品价格进行调整,A品牌足球的售价比第一次购买时提高5元,B品牌足球按第一次购买时售价的九折出售.如果学校此次购买A,B两种品牌足球的总费用不超过第一次花费的 , 且保证这次购买的B种品牌足球不少于33个,则这次学校有哪几种购买方案?